2. Þ функция общего вида.
3. Точки пересечения с координатными осями: c осью Ох: y = 0; x = 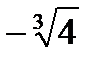
с осью Оу: x = 0; y – не существует.
4. х = 0 точка разрыва, 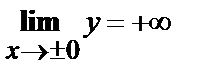 Þ прямая х = 0 вертикальная асимптота.
Þ прямая х = 0 вертикальная асимптота.
Наклонная асимптота в виде: y = kx + b. 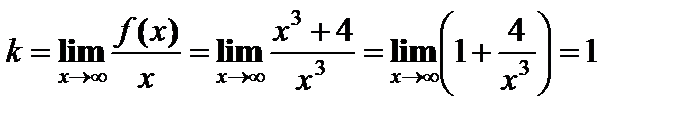 ,
,
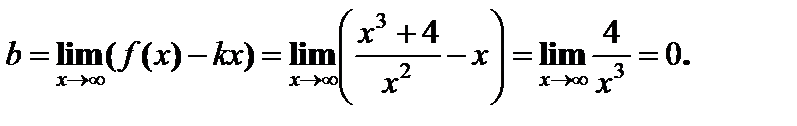
Наклонная асимптота у = х.
5. Интервалы возрастания-убывания, точки экстремума функции.
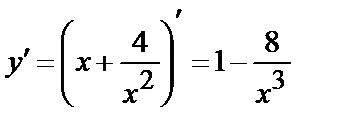 ,
, 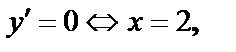
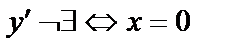 .
.
6. Для определения характера выпуклости функции находим вторую производную. 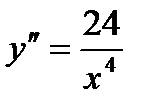
| x | 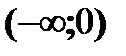
| 0 | (0;2) | 2 | (2;+¥) |
|
| y’ | + | 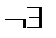
| – | 0 | + | |
| y’’ | + | 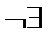
| + | + | + | |
| y | È | 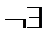
| È | 3 min | È | |
|
| ||||||
Пример 16. Провести исследование функции 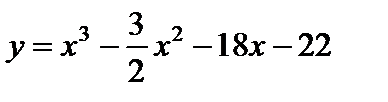 и построить её график.
и построить её график.
1. Область определения функции 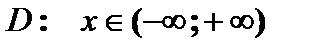 .
.
2. Чётность – нечётность:
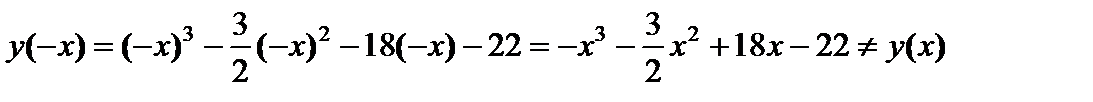 и
и 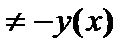 , значит, функция общего вида.
, значит, функция общего вида.
3. Точки пересечения графика с осями координат:
С осью 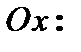
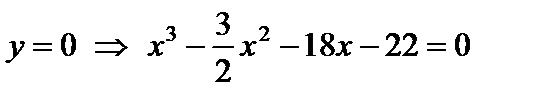 .
.
Корни многочлена являются делителями его свободного члена. Число 22 делится нацело на 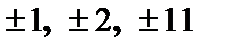 . Подставим эти числа поочерёдно в многочлен:
. Подставим эти числа поочерёдно в многочлен:
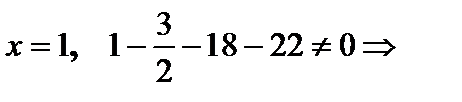
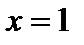 не является корнем.
не является корнем.
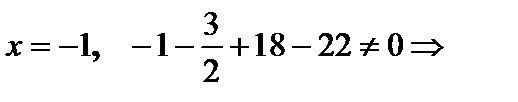
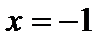 не является корнем.
не является корнем.
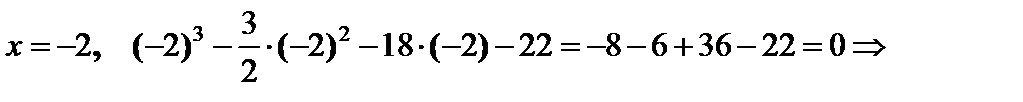
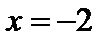 является корнем. Поэтому многочлен делится нацело на
является корнем. Поэтому многочлен делится нацело на 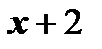 и его можно разложить на множители вида:
и его можно разложить на множители вида:
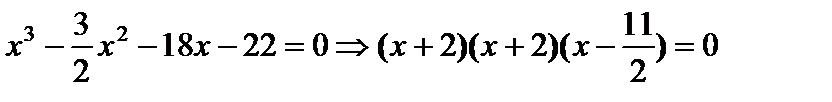 ,
,
Получаем точки пересечения с осью 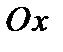 :
: 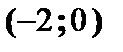 ,
, 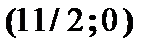 .
.
С осью 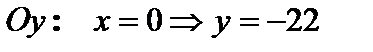 , т.е. точка
, т.е. точка 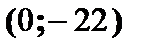 .
.
4. Точки экстремума и интервалы монотонности.
Найдём производную 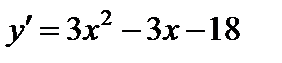 и точки, в которых производная равна нулю:
и точки, в которых производная равна нулю:
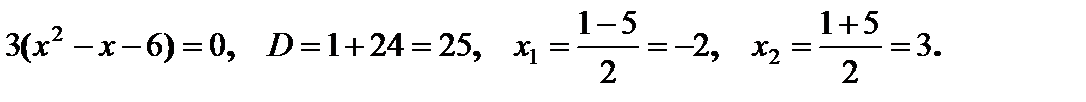
На числовой оси отмечаем точки 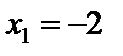 и
и 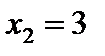 . Найдём знаки производной в полученных интервалах и укажем соответствующее поведение функции:
. Найдём знаки производной в полученных интервалах и укажем соответствующее поведение функции:
В интервалах 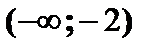 и
и 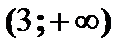 функция возрастает, в интервале
функция возрастает, в интервале 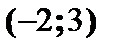 функция убывает. В точке
функция убывает. В точке 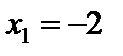 функция достигает максимума, а в точке
функция достигает максимума, а в точке 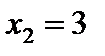 – минимума:
– минимума:
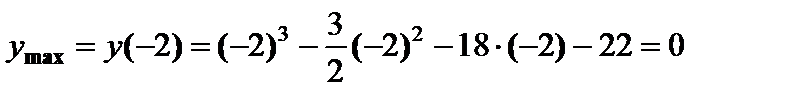 ,
, 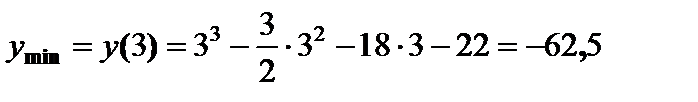 .
.
5. Интервалы выпуклости вверх-вниз и точки перегиба.
Найдём вторую производную функции 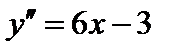 и точку, в которой производная равна нулю:
и точку, в которой производная равна нулю: 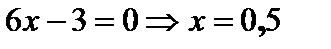 . Отметим эту точку на числовой оси, найдём знаки
. Отметим эту точку на числовой оси, найдём знаки 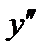 в полученных интервалах и укажем соответствующее поведение функции:
в полученных интервалах и укажем соответствующее поведение функции:
| В интервале 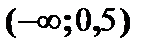 функция выпукла вверх, в интервале функция выпукла вверх, в интервале 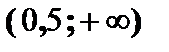 – выпукла вниз, точка – выпукла вниз, точка 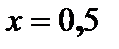 является точкой перегиба: является точкой перегиба:
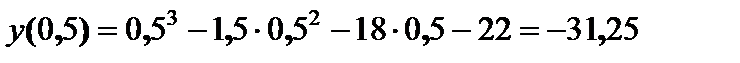 .
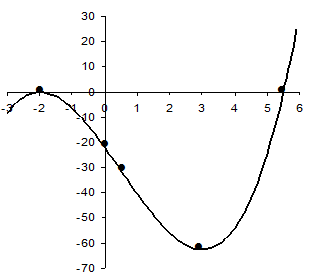
У данной функции асимптот нет. Проведённых исследований достаточно для построения графика. Отмечаем в системе координат точки пересечения с осями, точки экстремума и точку перегиба и соединяем их плавной линией. .
У данной функции асимптот нет. Проведённых исследований достаточно для построения графика. Отмечаем в системе координат точки пересечения с осями, точки экстремума и точку перегиба и соединяем их плавной линией.
|
Вопросы для повторения
1. Приращение функции 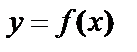 в точке
в точке 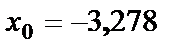 равно
равно 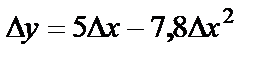 . Чему равна производная
. Чему равна производная 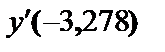 ?
?
2. Чему равна производная функции в точке 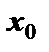 , если касательная к графику функции в точке
, если касательная к графику функции в точке 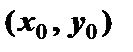 :
:
а) параллельна оси 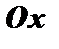 ; б) составляет с осью
; б) составляет с осью 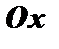 угол
угол 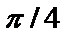 ; в) составляет с осью Oy угол 3300?
; в) составляет с осью Oy угол 3300?
3. Как найти угловой коэффициент касательной к графику функции 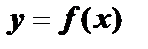 в точке с абсциссой x=5?
в точке с абсциссой x=5?
4. 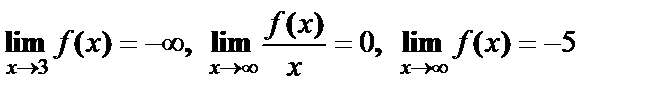 . Какие асимптоты есть у графика функции
. Какие асимптоты есть у графика функции 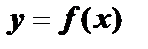 ?
?
5. Назовите основные правила дифференцирования.
6. Запишите таблицу производных основных элементарных функций.
7. В каких случаях приращение функции можно заменить её дифференциалом? Где это используется?
8. Как связан знак производной с возрастанием и убыванием функции?
9. Назовите необходимое и достаточное условия экстремума.
10. Чем отличается максимум от наибольшего значения функции, а минимум от её наименьшего значения?
11.Что такое точка перегиба графика функции?
12. В каких случаях при вычислении предела функции можно применить правило Лопиталя?









