Минимум и максимум функции называются точками экстремума.
6.1. Производная, её геометрический и физический смысл
Дифференцирование функции – вычисление производной.
Дифференцируемая функция – функция, у которой есть производная.
| Определение производной.
| ||
| Геометрический смысл производной: значение производной функции | ||
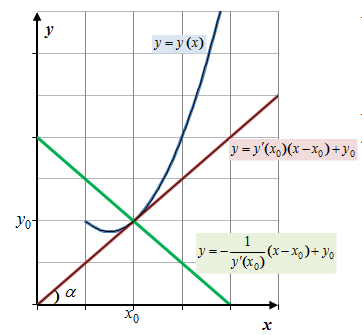
| Уравнение касательной к графику функции
Уравнение нормали к графику функции
Нормаль Угол между кривыми
| |
| 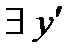 в точке в точке 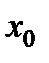 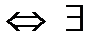 касательная к графику функции в точке касательная к графику функции в точке 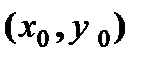 . .
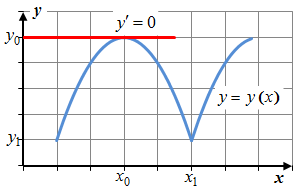
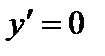 в точке в точке 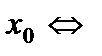 касательная параллельна оси Ох. В т. касательная параллельна оси Ох. В т. 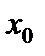 функция достигает максимума: функция достигает максимума: 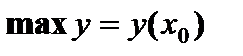
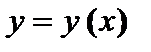 непрерывна в точке непрерывна в точке 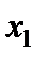 , но , но 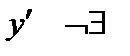 в точке в точке 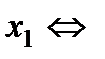 нет касательной в точке нет касательной в точке 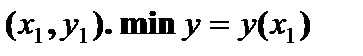
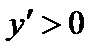 при при 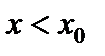 и при и при 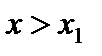 (функция возрастает) (функция возрастает)
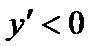 при при 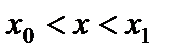 (функция убывает) (функция убывает)
| |
| Физический смысл производной: | ||
6.2 Вычисление производной. Дифференциал
I . Правила дифференцирования. 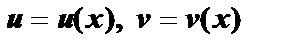 – дифференцируемые функции
– дифференцируемые функции
1. Константа: 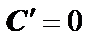 ;
;
2. 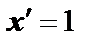 ;
;
3. Сумма (разность): 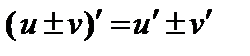 ;
;
4. Произведение: 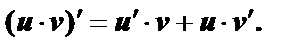
5. Константа умножить на функцию: 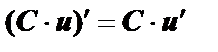 ;
;
6. Частное: 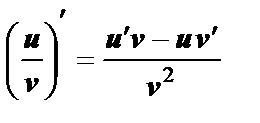 ;
;
7. Константа разделить на функцию: 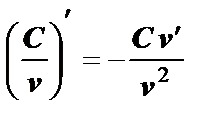 .
.
| II . Таблица производных | ||||||
| Степенные функции 1. 2. 3. 4. Показательные функции 5. 6. Логарифмические функции 7. 8. | Тригонометрические функции 9. 10. 11. 12. Гиперболические функции 13. 14. 15. 16. | Обратные тригонометрические функции 17. 18. 19. 20. | ||||
| Производные высших порядков | ||||||
| Вторая производная n-ая производная | ||||||
| Производные параметрически заданной функции | ||||||
| Дифференциал | ||||||
|
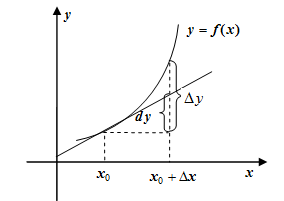
| 1. Геометрический смысл дифференциала:
2. 3. 4. 5. 6. 7. 8. | |||||
| 9. Формула приближённых вычислений : | ||||||
| Погрешности вычисления Найти
| ||||||
| 6.3 Теоремы о среднем. Правило Лопиталя | ||||||
|
| Теорема Ролля . Функция 1. непрерывна на [a;b]; 2. дифференцируема в интервале (a;b); 3. Тогда существует по крайней мере одна точка Геометрический смысл: касательная к графику функции в точке | |||||
|
| Теорема Лагранжа . Функция 1. непрерывна на [a;b]; 2. дифференцируема в интервале (a;b). Тогда существует по крайней мере одна точка
Геометрический смысл: касательная к графику функции в точке | |||||
| Теорема Коши. Функции 1. непрерывны на [a;b]; 2. дифференцируемы в интервале (a;b); 3. Тогда существует по крайней мере одна точка
| ||||||
| Раскрытие неопределённостей в пределах | ||||||
| Правило Лопиталя. Функции 1. удовлетворяют условиям теоремы Коши в некоторой окрестности точки 2. | ||||||
| Раскрытие других видов неопределенностей | ||||||
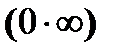
|
| |||||
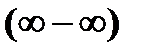
|
| |||||
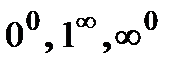
|
| |||||
| Формула Тейлора. Функция где Формула Маклорена:
| ||||||
6.4 Приложение производных к исследованию функций
Определение. Функция имеет локальный максимум (минимум) в точке 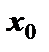 , если она определена в точке
, если она определена в точке 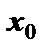 и некоторой ее окрестности
и некоторой ее окрестности 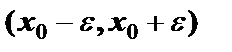 , и значение функции в точке
, и значение функции в точке 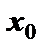 больше (меньше), чем ее значение во всех соседних точках:
больше (меньше), чем ее значение во всех соседних точках: 
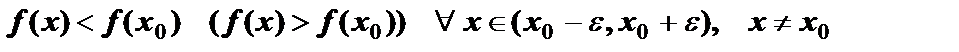 .
.
Минимум и максимум функции называются точками экстремума.
| Определение. Функция | Функция выпукла вверх Функция выпукла вниз | |||
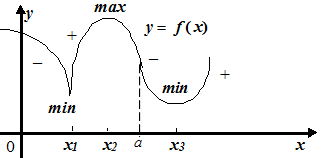
| Исследование по первой производной
| |||
| Исследование по второй производной | ||||
|
| Если вторая производная существует, то в точке максимума В точке перегиба | |||
| План исследования функции | ||||
| 1. Область определения. 2. Чётность: 3. Асимптоты: 1) вертикальные асимптоты вида 4. Точки пересечения с осями: с 5. Интервалы монотонности и точки экстремума (по знаку первой производной 6. Интервалы выпуклости вверх (вниз) и точки перегиба (по знаку второй производной 7. Построение графика. | ||||
| Наибольшее M и наименьшее m значения непрерывной функции, заданной на отрезке [ a ; b ] | ||||
|
Наибольшее и наименьшее значения непрерывной функции, заданной на отрезке | ||||
6.5 Примеры решения задач
Пример 1. Найти уравнения касательной и нормали к кривой 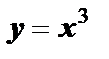 в точке с абсциссой
в точке с абсциссой 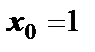 .
.
Решение. Уравнения касательной и нормали – формулы (6.2) и (6.3).
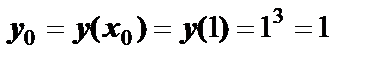 .
. 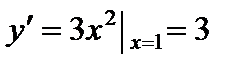 .
.
Уравнение касательной: 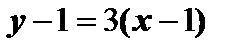 или
или 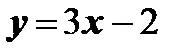 .
.
Уравнение нормали: 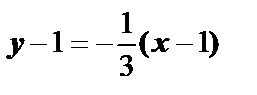 или
или 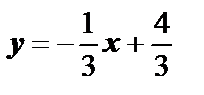 .
.
Пример 2. Найти вторую производную 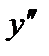 функции
функции 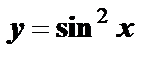 и вычислить её в точке
и вычислить её в точке 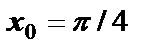 .
.
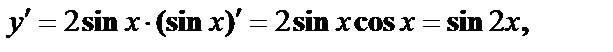
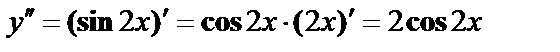 ,
,
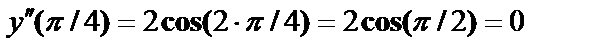 .
.
Пример 3. Исследовать функцию 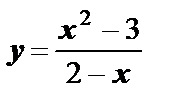 и построить её график.
и построить её график.
Решение. Проведём полное исследование функции.
1. Область определения 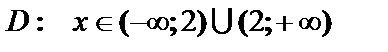 .
.
2. 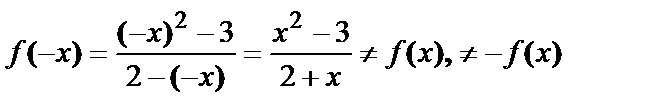 . В этом случае говорят, что функция
. В этом случае говорят, что функция 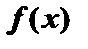 общего вида.
общего вида.
3. Асимптоты. Исследуем точку разрыва 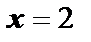 на наличие в ней вертикальной асимптоты. Для этого найдём пределы функции слева и справа. Если хотя бы один предел будет равен бесконечности, то в точке
на наличие в ней вертикальной асимптоты. Для этого найдём пределы функции слева и справа. Если хотя бы один предел будет равен бесконечности, то в точке 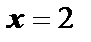 будет проходить вертикальная асимптота.
будет проходить вертикальная асимптота.
Предел слева: 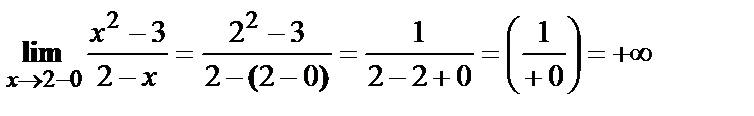 ,
Предел справа: ,
Предел справа: 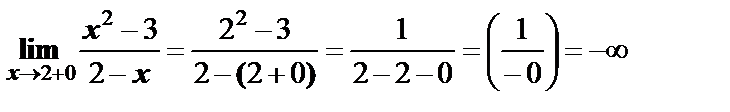 . .
| Прямая 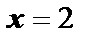 – вертикальная асимптота. – вертикальная асимптота.
|
Наклонная асимптота 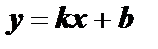 :
:
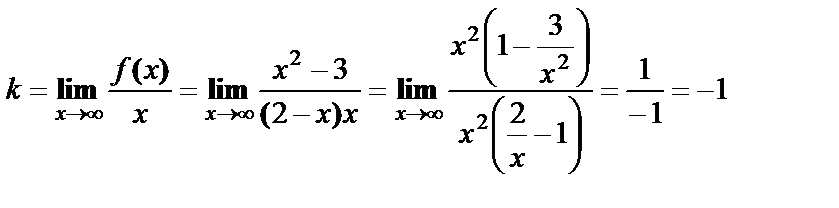 ,
, 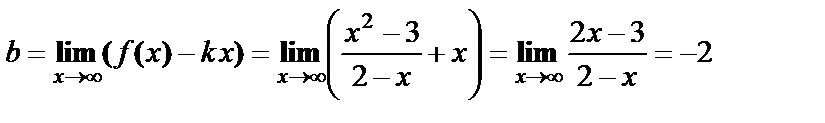 .
.
Таким образом, прямая 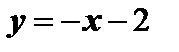 является наклонной асимптотой графика исследуемой функции.
является наклонной асимптотой графика исследуемой функции.
4. Точки пересечения с осями.
С осью 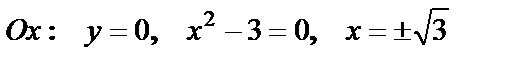 , т.е. точки
, т.е. точки 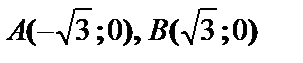 .
.
С осью 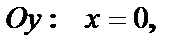
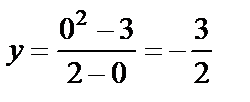 , т.е. точка
, т.е. точка 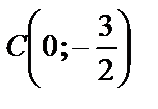 .
.
5. Интервалы монотонности. Найдём производную 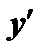 и точки, в которых она равна нули или не существует.
и точки, в которых она равна нули или не существует.
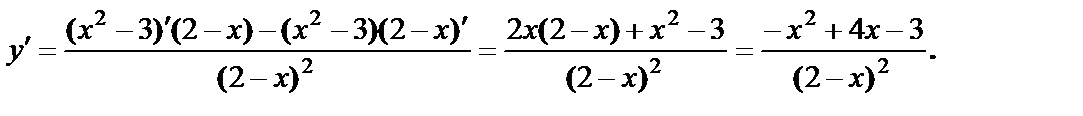
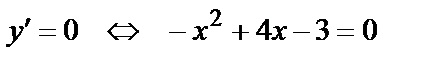 ,
, 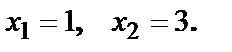
 ,
, 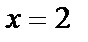 .
.
6. Интервалы выпуклости вверх (вниз).
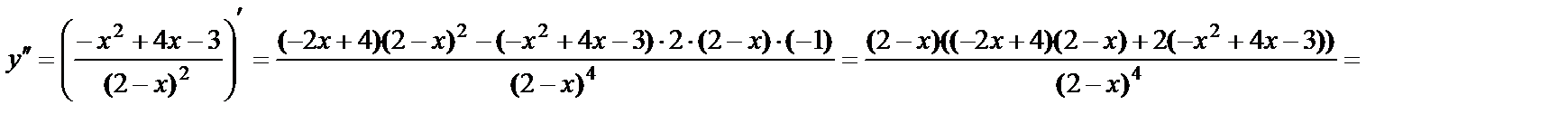
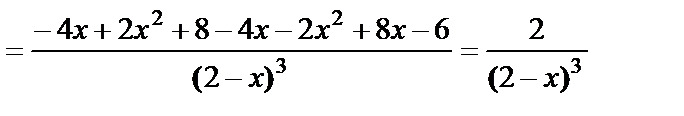 .
.
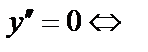 таких точек нет;
таких точек нет; 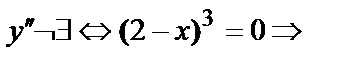
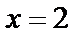 .
.
Найденные точки разбивают всю числовую ось на четыре интервала. Определим знаки первой и второй производной и поведение функции в каждом интервале.
| x | 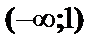
| 1 | 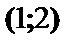
| 2 | 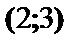
| 3 | 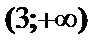
|
| y’ | – | 0 | + | 
| + | 0 | – |
| y’’ | + | + | + | 
| – | – | – |
| y | 
| –2 min | 
| 
| 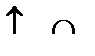
| –6 max | 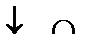
|
В точке 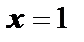 функция достигает минимума, в точке
функция достигает минимума, в точке 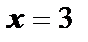 – максимума:
– максимума:
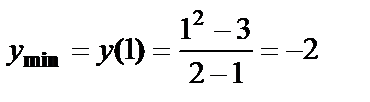 ,
, 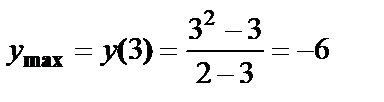 .
.
| | 7. Для построения графика отмечаем точки пересечения с осями координат, точки экстремума и пунктирными линиями наносим асимптоты. Начинаем построение от вертикальной асимптоты. При 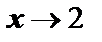 слева предел функции равен слева предел функции равен 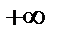 , а при , а при 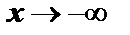 график функции приближается к наклонной асимптоте график функции приближается к наклонной асимптоте 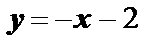 . Справа от вертикальной асимптоты . Справа от вертикальной асимптоты 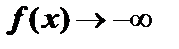 , а при , а при 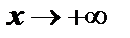 график функции приближается к наклонной асимптоте. график функции приближается к наклонной асимптоте.
|
Пример 4. Дана функция 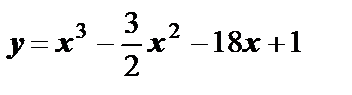 . Найти: 1) экстремум функции;
. Найти: 1) экстремум функции;
2) наибольшее M и наименьшее m значения функции на отрезке [-1, 4].
Решение.1) 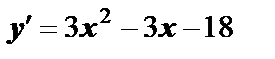 . Находим точки, в которых производная равна нулю:
. Находим точки, в которых производная равна нулю:
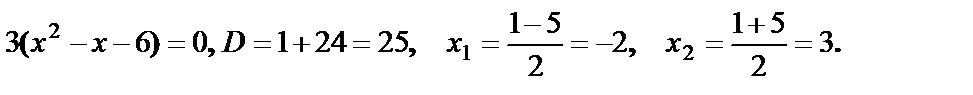
На числовой оси отмечаем точки 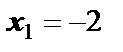 и
и 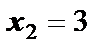 . Находим знаки производной в полученных интервалах и указываем соответствующее поведение функции:
. Находим знаки производной в полученных интервалах и указываем соответствующее поведение функции:
В точке 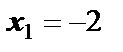 функция достигает максимума, в точке
функция достигает максимума, в точке 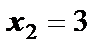 – минимума:
– минимума:
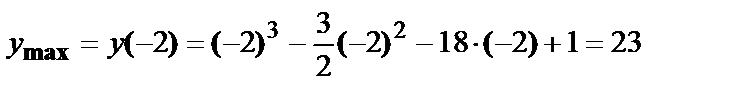 .
. 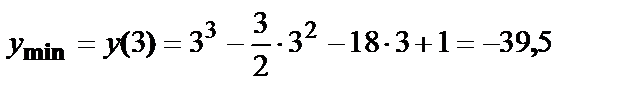 .
.
2) Вначале нужно найти точки, в которых производная функции равна нулю или не существует. Это 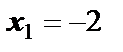 и
и 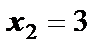 . Но точка
. Но точка 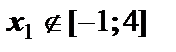 , поэтому дальше её не рассматриваем. Затем необходимо вычислить значение функции в концах отрезка и в точке
, поэтому дальше её не рассматриваем. Затем необходимо вычислить значение функции в концах отрезка и в точке 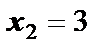 , т.к. она принадлежит отрезку
, т.к. она принадлежит отрезку 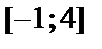 . После этого из полученных значений нужно выбрать самое большое M и самое маленькое m значения.
. После этого из полученных значений нужно выбрать самое большое M и самое маленькое m значения.
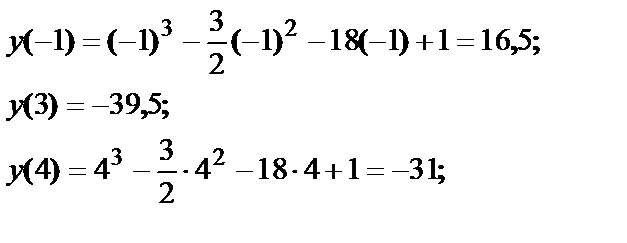
Таким образом, 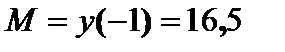 ,
, 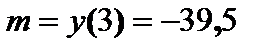 .
.
Пример 5. Найти производные функций.
1) 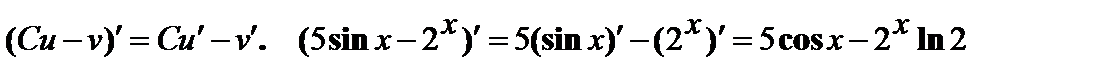 .
.
2) производная суммы (разности) степенных функций:
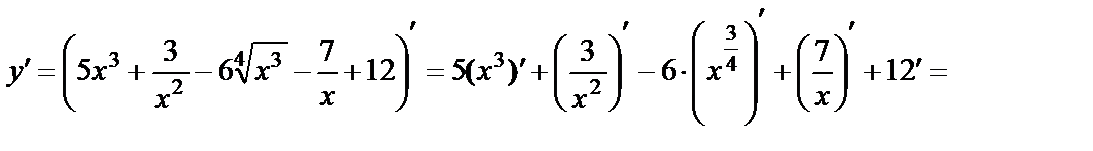
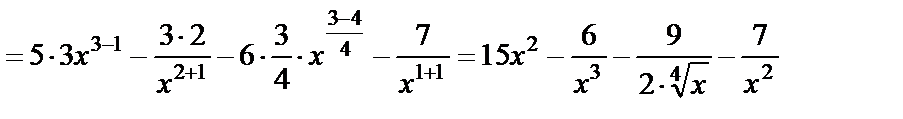 .
.
3) производная произведения: 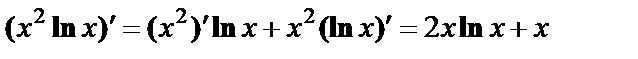 .
.
4) производная частного:
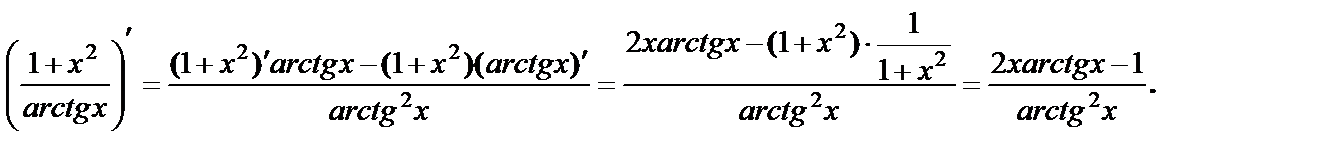
Пример 6. Выяснить, в какой точке кривой 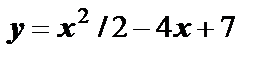 касательная параллельна прямой
касательная параллельна прямой 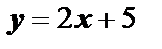 . Найти уравнение касательной в этой точке.
. Найти уравнение касательной в этой точке.
Решение. Угловой коэффициент прямой 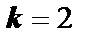 равен угловому коэффициенту касательной, так как они параллельны:
равен угловому коэффициенту касательной, так как они параллельны: 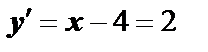 . Тогда
. Тогда  ,
, 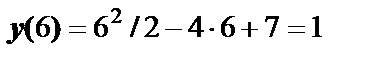 . В точке
. В точке 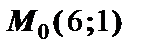 касательная к кривой
касательная к кривой 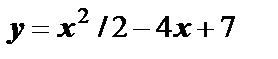 параллельна прямой
параллельна прямой 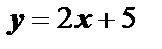 , её уравнение имеет вид
, её уравнение имеет вид 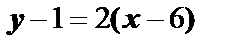 или
или 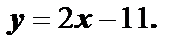
Пример 7. Найти точку на кривой 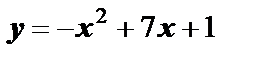 , в которой касательная составляет угол
, в которой касательная составляет угол 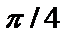 с положительным направлением оси
с положительным направлением оси 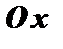 . Написать уравнение этой касательной.
. Написать уравнение этой касательной.
Решение. Угловой коэффициент касательной 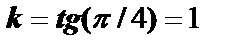 равен производной
равен производной 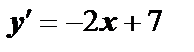 рассматриваемой функции, поэтому
рассматриваемой функции, поэтому 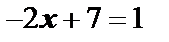 ,
, 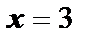 ,
, 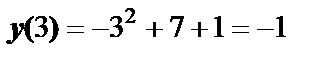 . Тогда в точке
. Тогда в точке 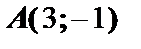 рассматриваемой кривой
рассматриваемой кривой 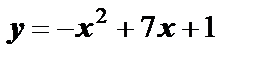 касательная составляет угол
касательная составляет угол 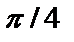 с положительным направлением оси
с положительным направлением оси 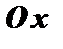 . Её уравнение
. Её уравнение 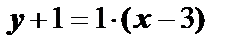 , или
, или 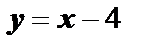 .
.
Пример 8. Тело движется по прямой по закону 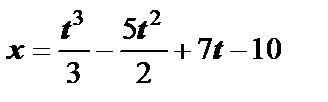 . Определить скорость и ускорение движения тела в момент времени
. Определить скорость и ускорение движения тела в момент времени 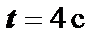 .
.
Решение. Скорость тела равна производной пути по времени, ускорение – производная скорости: 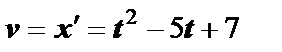 ,
, 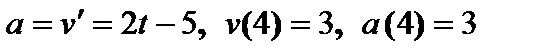 .
.
Пример 9. Вычислить приращение длины стороны куба, если известно, что его объём увеличился от 64 до 64,3 м3.
Решение. Если 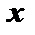 – объём куба, то его сторона
– объём куба, то его сторона 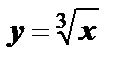 . По условию задачи
. По условию задачи 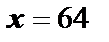 ,
, 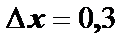 . Тогда приращение стороны куба
. Тогда приращение стороны куба 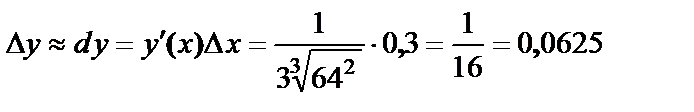 м.
м.
Пример 10. Найти асимптоты и построить график функции 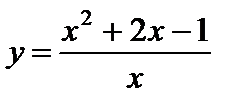 .
.
1) область определения D=(-¥;0) È (0;+ ¥). Вертикальная асимптота в точке разрыва х=0:
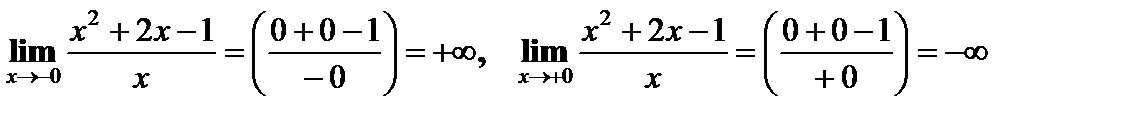 ,
,
следовательно, х = 0- вертикальная асимптота.
2) Наклонная асимптота:
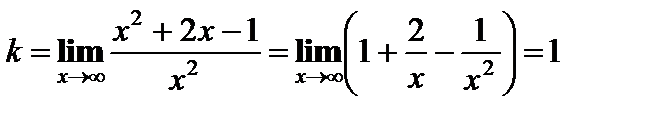
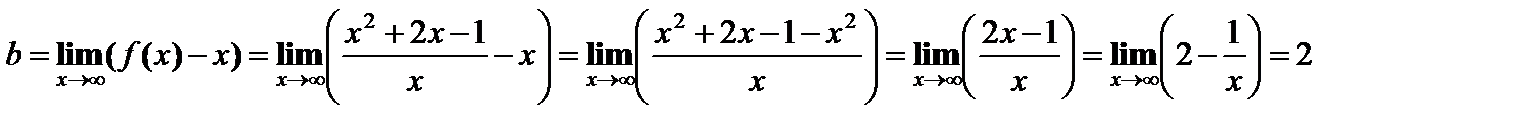
Т.о., прямая у = х + 2 – наклонная асимптота.
Построим график функции:
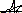
Пример 11. Найти асимптоты и построить график функции 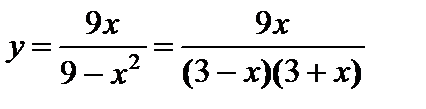 .
.
1) Область определения D=(-¥;-3) È (-3;3) È (3;+ ¥). Вертикальные асимптоты в точках разрыва.
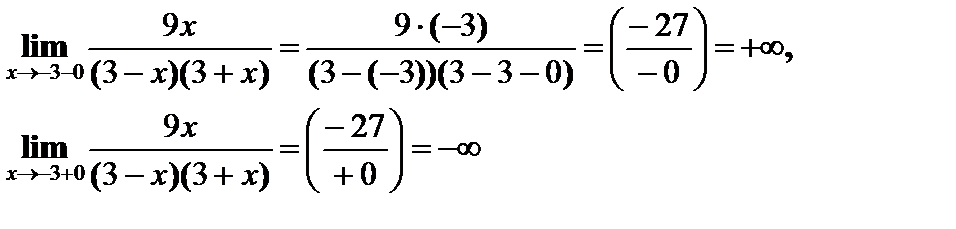
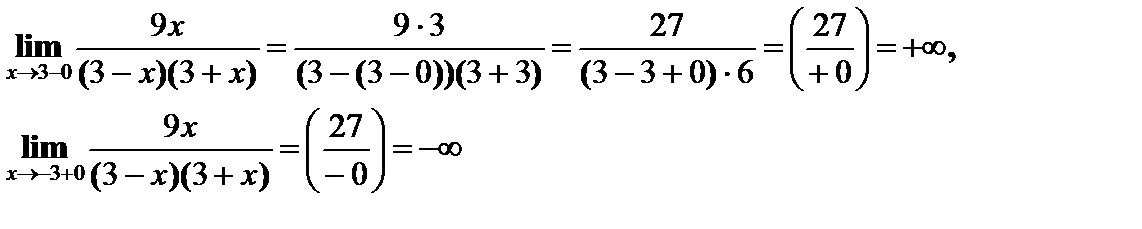
Прямые х = 3 и х = -3 – вертикальные асимптоты кривой.
Степень числителя меньше степени знаменателя, поэтому наклонной асимптоты нет. Найдем горизонтальную:
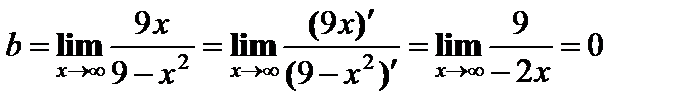
y = 0 – горизонтальная асимптота.
Пример 12. Найти асимптоты и построить график функции 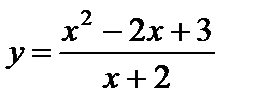 .
.
1) D=(-¥; –2) È (–2;+ ¥).
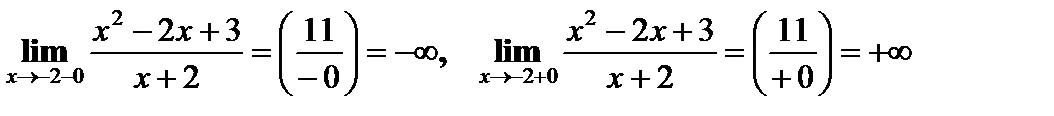
Прямая х = –2 – вертикальная асимптота кривой.
Найдем наклонные асимптоты.
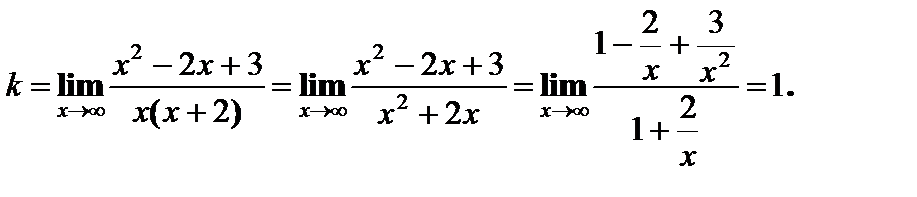
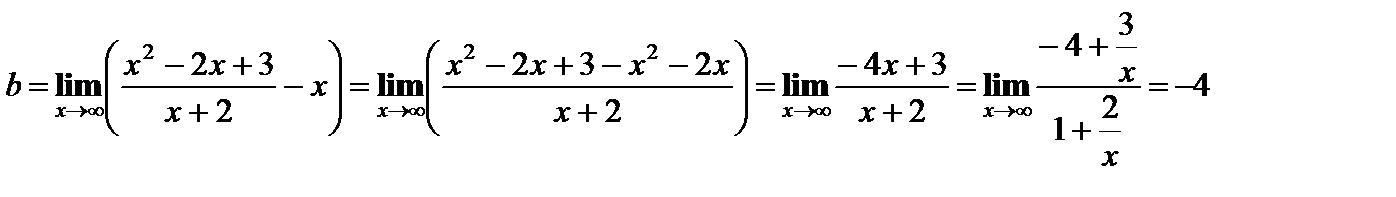
Прямая у = х – 4 является наклонной асимптотой.

Пример 13. Исследовать функцию 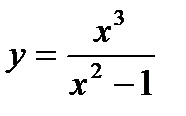 и построить ее график.
и построить ее график.
1) Область определения D= (-¥; -1) È (-1; 1) È (1; ¥). х = 1, х = –1 – точки разрыва.
2) Асимптоты. В точках разрыва вертикальные асимптоты.
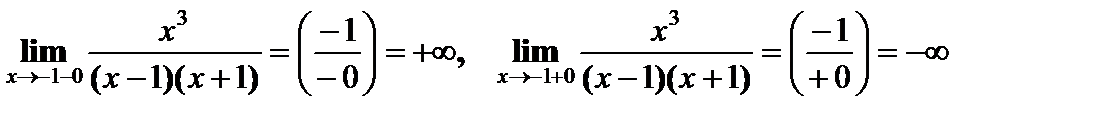
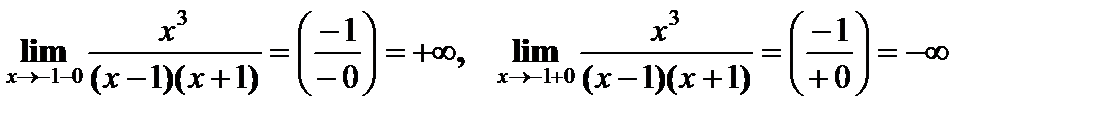
Прямые х = 1, х = –1 являются вертикальными асимптотами кривой.
Наклонная асимптота.
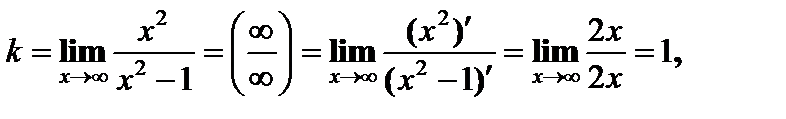
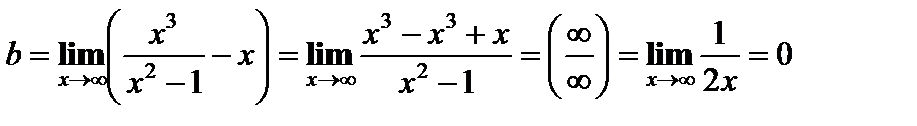
y = x – наклонная асимптота.
3) Четность – нечетность. 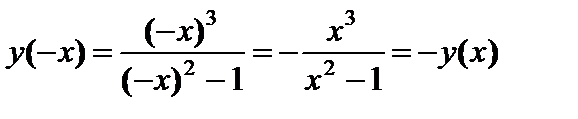 – нечётная функция. Значит, график симметричен относительно начала координат.
– нечётная функция. Значит, график симметричен относительно начала координат.
4) Точки пересечения с осями. С осью Ox: y=0, 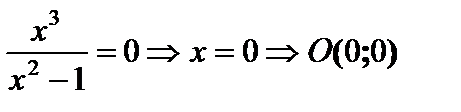 . С осью Oy та же точка.
. С осью Oy та же точка.
5) Интервалы монотонности и точки экстремума. Найдем производную функции
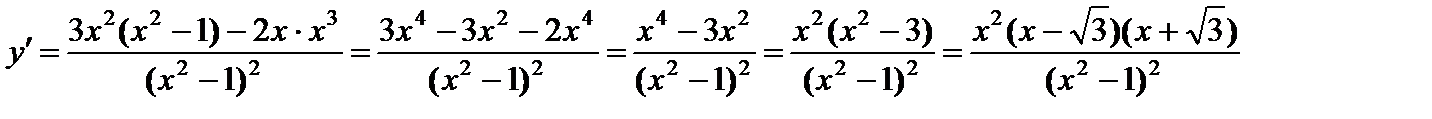 ,
,
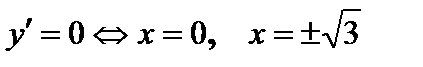
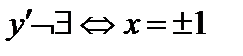
6) Интервалы выпуклости вверх – вниз, точки перегиба. Найдем вторую производную функции
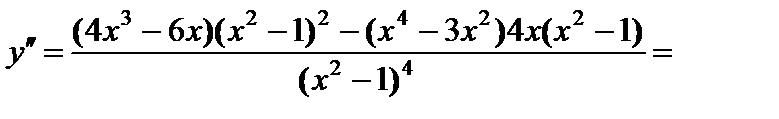
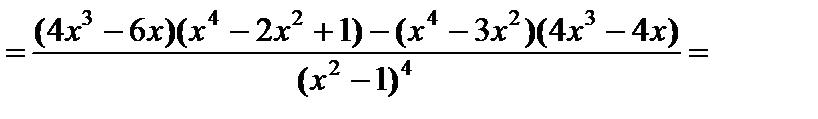
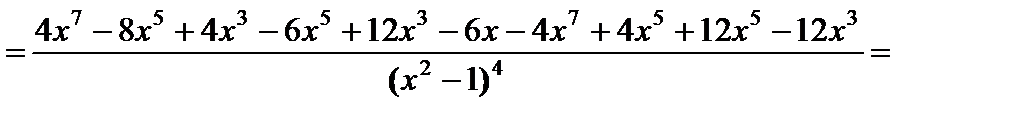
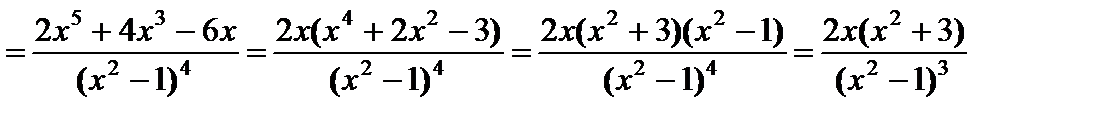 .
.
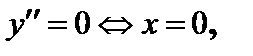
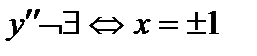
Заполним таблицу:
| x | 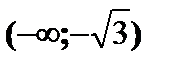
| 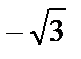
| 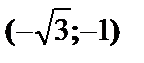
| 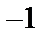
| 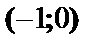
| 0 | 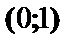
| 1 | 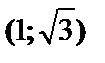
| 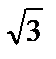
| 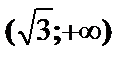
|
| y’ | + | 0 | – | 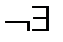
| – | 0 | – | 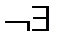
| – | 0 | + |
| y’’ | – | – | – | 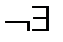
| – | 0 | – | 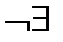
| – | – | – |
| y | Ç | 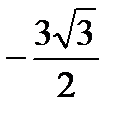 max
max
| Ç | 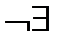
| Ç | 0 Точка перегиба | È | 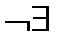
| È | 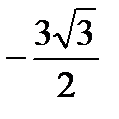 min
min
| È |

Пример 14. Исследовать функцию 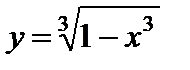 и построить ее график.
и построить ее график.
1). D= ( –¥; +¥).
2). 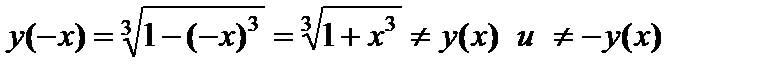 Þ Функция общего вида.
Þ Функция общего вида.
3). Точки пересечения с координатными осями: c осью Оу: x = 0; y = 1;
с осью Ох: y = 0; x = 1.
4). Точки разрыва и асимптоты: Вертикальных асимптот нет.
Наклонные асимптоты: общее уравнение y = kx + b;
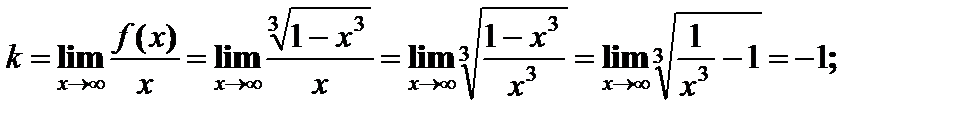
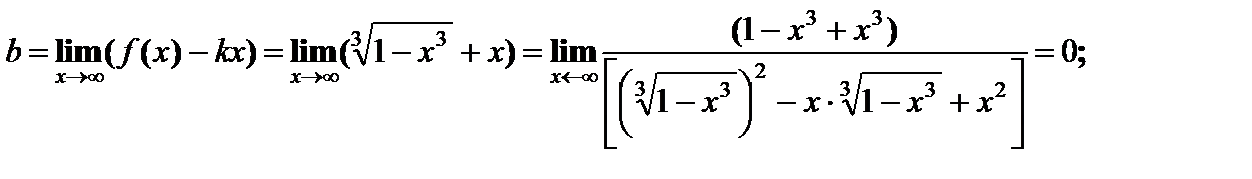
у = –х – наклонная асимптота.
5). Возрастание и убывание функции, точки экстремума.
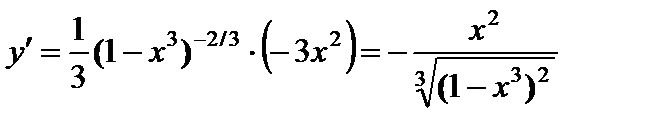 .
. 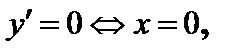
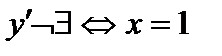 .
.
6) Выпуклость вверх-вниз, точки перегиба.
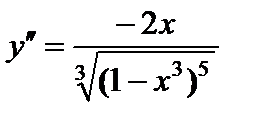 .
. 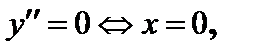
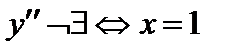 .
.
| x | 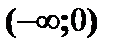
| 0 | (0;1) | 1 | (1;+¥) |
|
| y’ | – | 0 | – | 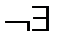
| – | |
| y’’ | + | 0 | – | 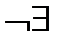
| + | |
| y | È | 1 Точка перегиба | Ç | 0 Точка перегиба | È | |
|
| ||||||
Пример 15. Исследовать функцию 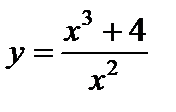 и построить ее график.
и построить ее график.
1. D= ( –¥; 0) È (0;+¥)..









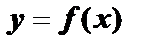 – непрерывная функция.
– непрерывная функция. 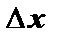 – приращением аргумента. Разность
– приращением аргумента. Разность 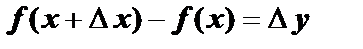 – приращение функции. Производная равна пределу отношения приращения функции к приращению аргумента при стремлении последнего к нулю:
– приращение функции. Производная равна пределу отношения приращения функции к приращению аргумента при стремлении последнего к нулю: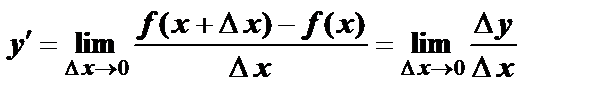 (6.1)
(6.1) 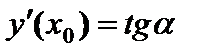 в точке
в точке 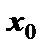 равно тангенсу угла наклона (угловому коэффициенту) касательной к графику функции
равно тангенсу угла наклона (угловому коэффициенту) касательной к графику функции 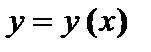 в точке
в точке 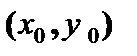 .
. 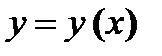 в точке
в точке 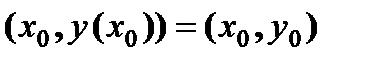 :
: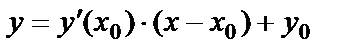 (6.2)
(6.2)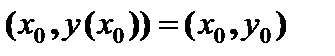 :
: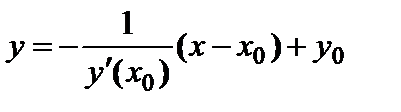 (6.3)
(6.3)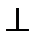 касательной в точке
касательной в точке 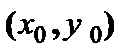
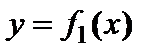 и
и 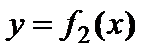 в точке пересечения
в точке пересечения 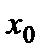 :
: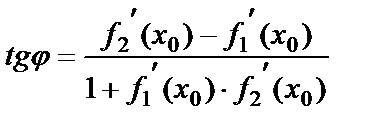 .
.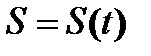 – путь,
– путь, 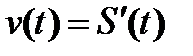 – скорость,
– скорость, 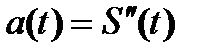 – ускорение.
– ускорение.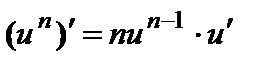 ;
;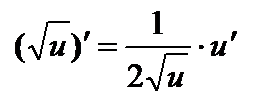 ;
;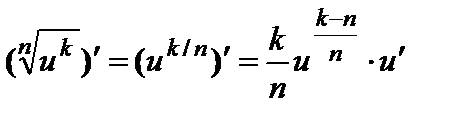 ;
;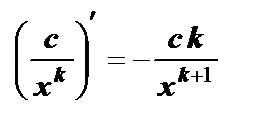 ;
;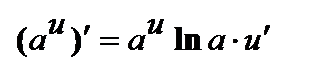 ;
;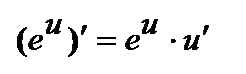 ;
;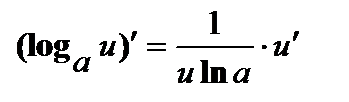 ;
;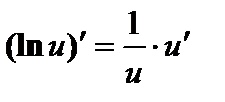 ;
;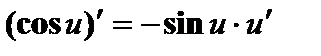 ;
;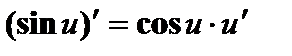 ;
;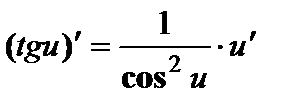 ;
;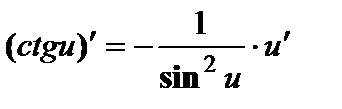 ;
;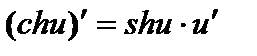 ;
;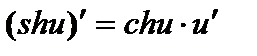 ;
;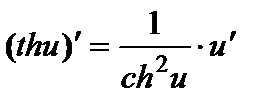 ;
;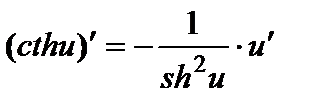 ;
;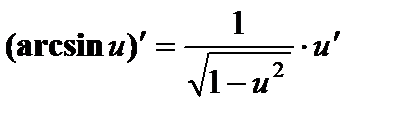 ;
;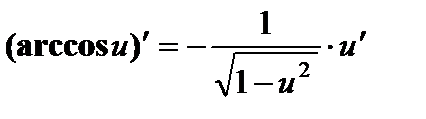 ;
;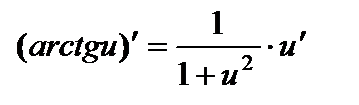 ;
;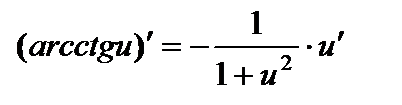 ;
;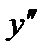 – это производная от первой производной:
– это производная от первой производной: 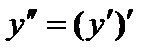 .
.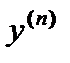 – это производная от (n- 1)-ой производной:
– это производная от (n- 1)-ой производной: 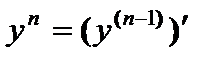 .
.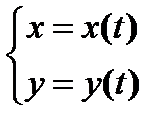
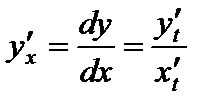 ,
, 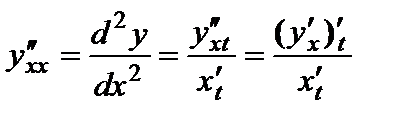
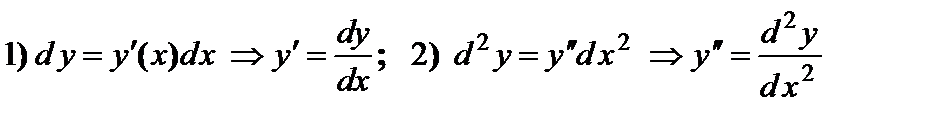
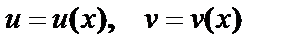 – дифференцируемые функции
– дифференцируемые функции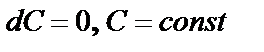 ;
;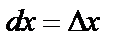 , если x – независимая переменная;
, если x – независимая переменная;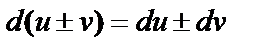 ;
;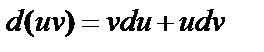 ;
;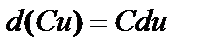 ;
;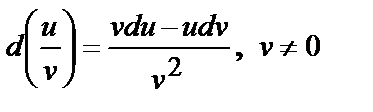 ;
;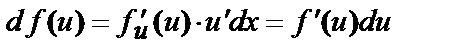 .
.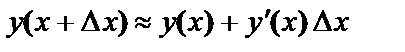 (6.4)
(6.4) 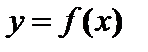 , если
, если 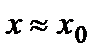 . Тогда
. Тогда 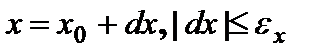 ,
, 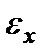 – абсолютная погрешность x. Тогда
– абсолютная погрешность x. Тогда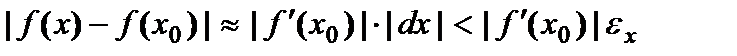 .
.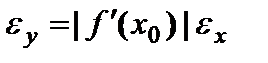 – абсолютная погрешность функции
– абсолютная погрешность функции 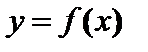
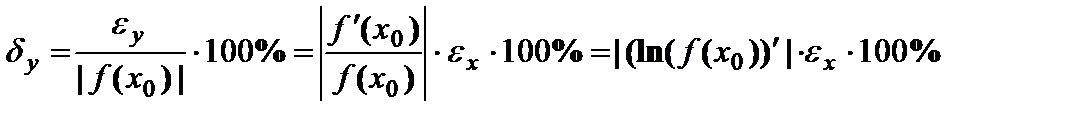 – относительная погрешность y.
– относительная погрешность y.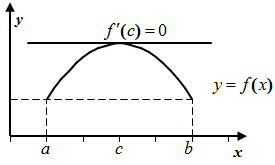
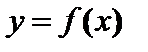
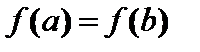 .
.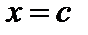
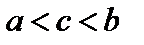 ), такая, что
), такая, что 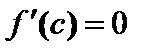 .
.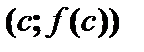 параллельна оси Ox.
параллельна оси Ox.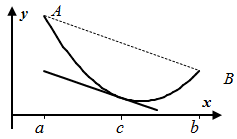
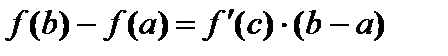 .
.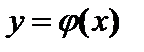
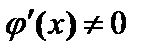 при
при 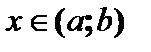 .
.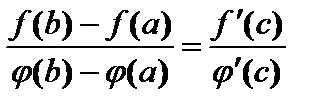 .
.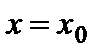 ;
;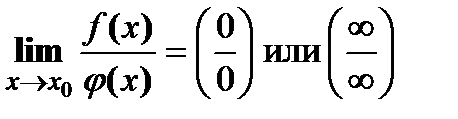 и существует
и существует 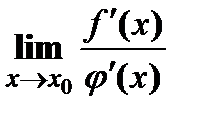 . Тогда
. Тогда 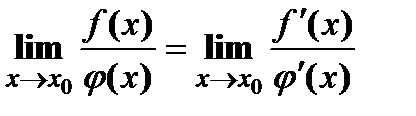 .
.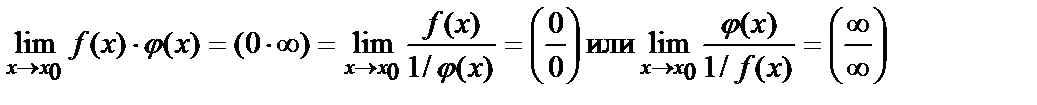
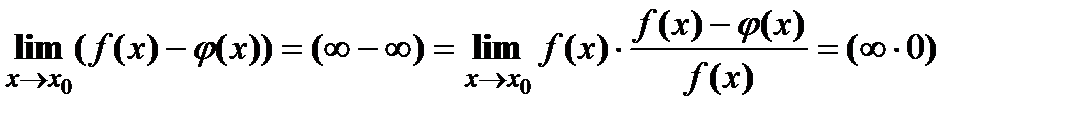
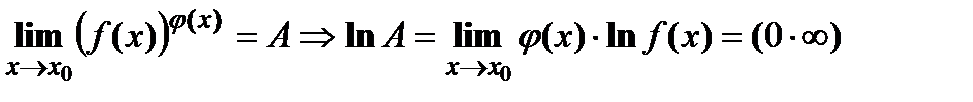
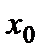 и её окрестности
и её окрестности 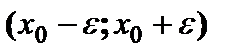 и имеет в ней производные до порядка (n+1) включительно. Тогда
и имеет в ней производные до порядка (n+1) включительно. Тогда 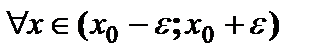
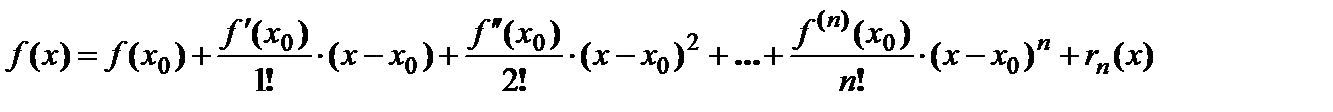 , (6.5)
, (6.5)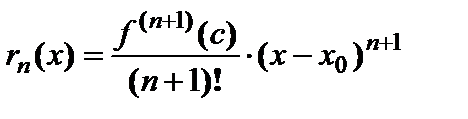 – остаточный член в форме Лагранжа.
– остаточный член в форме Лагранжа.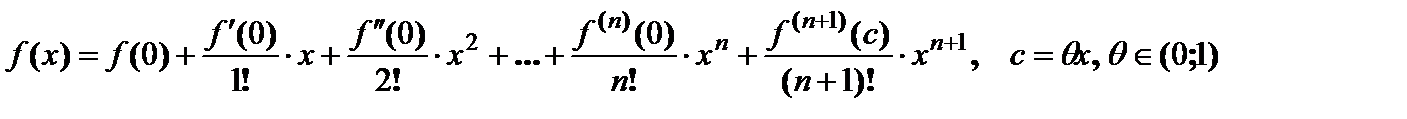 . (6.6)
. (6.6)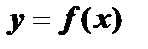 называется выпуклой вверх (выпуклой вниз) на множестве
называется выпуклой вверх (выпуклой вниз) на множестве 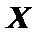 , если её график находится ниже (выше) любой касательной.
, если её график находится ниже (выше) любой касательной.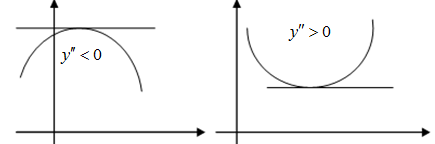
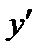
 Функция убывает.
Функция убывает.  Функция возрастает
Функция возрастает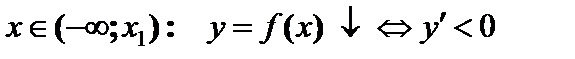
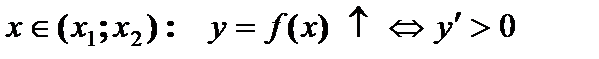
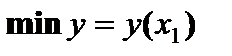 .
. 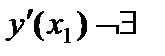 . При переходе через точку минимума
. При переходе через точку минимума 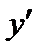 меняет знак с «–» на «+»
меняет знак с «–» на «+»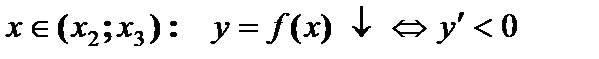
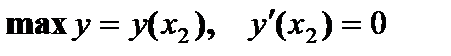 . При переходе через точку максимума
. При переходе через точку максимума 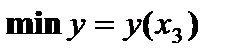 .
. 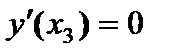
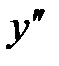 .
.  функция выпукла вверх,
функция выпукла вверх,  – выпукла вниз
– выпукла вниз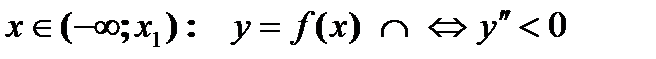
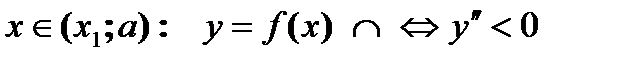
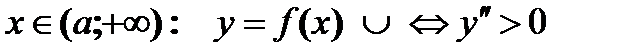
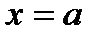 – точка перегиба
– точка перегиба  , в точке минимума
, в точке минимума 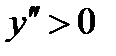 .
.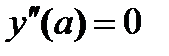 .
.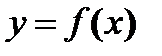 и построение её графика
и построение её графика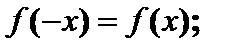 нечётность:
нечётность: 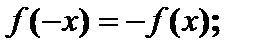 иначе – функция общего вида.
иначе – функция общего вида.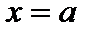 в точках разрыва 2-го рода;
в точках разрыва 2-го рода; 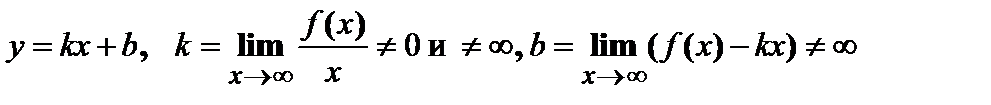 ;
; 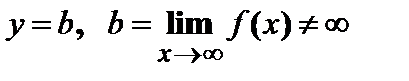 .
.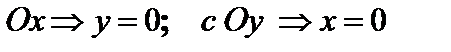 .
.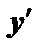 ).
).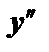 ).
).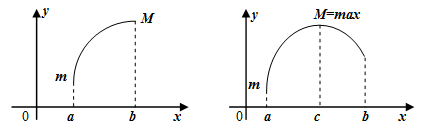
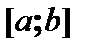 , находятся либо в концах отрезка, либо внутри отрезка в точках экстремума.
, находятся либо в концах отрезка, либо внутри отрезка в точках экстремума.