Таблица 0.4:Значения параметра , используемого для проверки равенства средних двух совокупностей.

Дата: 2025-05-25; Просмотры: 3
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

a=0,10 a=0,05 a=0,025 a=0,01 a=0.005
1 6.314 12.706 25.452 63.657 127.30
2 2.920 4.303 6.205 9.925 14.089
3 2.353 3.182 4.177 5.841 7.453
4 2.132 2.776 3.495 4.604 5.597
5 2.015 2.571 3.163 4.032 4.773
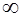
1.645 1.96 2.241 2.576 2.807

Если справедливо неравенство 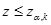, то поставленную гипотезу о том, что средние значения совпадают, не отвергают. При этом вероятность совершить ошибку равна заданному значению .

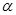Если дисперсии генеральных совокупностей не равны, т.е. 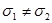, то равенство двух средних проверяют с помощью приближенного 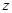-критерия, который вычисляют из соотношения

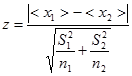, (0.27)

число степеней свободы при этом определяют из выражения

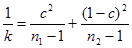, где 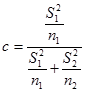(0.28)

Если выполняется неравенство 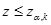, то гипотезу 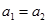с вероятностью совершить ошибку равной заданному значению 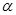, не отвергают. В противном случае 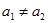. И в этом случае вероятность совершить ошибку равна заданному значению .

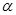Рассмотрим применение данного критерия на следующем примере. Пусть в результате проведения измерений получены значения следующие значения импульсов шаров до и после столкновения

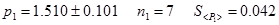- импульс до столкновения.

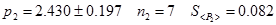- импульс после столкновения.

Проверим гипотезу о том, импульсы шаров до и после столкновения равны.

1. Вычисляем параметр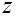

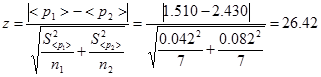
2. Определяем число степеней свободы по формуле: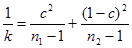

Вначале находим параметр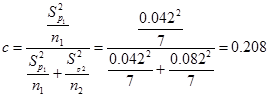

Затем вычисляем параметр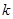

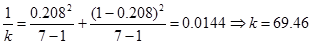
3. По табл. 0.4 для заданного значения вероятности совершить ошибку ( 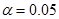) находим параметр : .

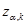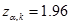4. Так как 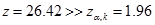то гипотезу о равенстве средних значений двух генеральных совокупностей ( 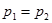) с вероятностью совершить ошибку 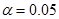необходимо отвергнуть. Делаем вывод: в данном эксперименте импульс шаров до и после столкновения не равны.

Лабораторная работа 0-1(1): Определение ускорение свободного падения с помощью математического маятника.

Упражнение 1. Порядок обработки прямых измерений. Определение периода колебаний математического маятника.

1. Получите у преподавателя значения длины нити математического маятника 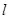и числа измерений 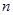периода колебаний.

2. Проведите 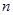измерений периода колебаний маятника, результаты этих измерений внесите в табл.0.4.

Таблица 0.4

N изм 1 2 3 4 5

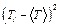
3. Просуммируйте все значения 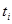и данную сумму занесите в соответствующую графу 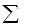. Используя значение этой суммы, по формуле (0.1) найдите среднее значение периода колебаний математического маятника.

4. Зная 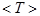, заполните окончательно табл.0.4, используя данные этой таблицы, найдите дисперсию среднего значение периода колебаний маятника по формуле (0.3).

5. Найдите среднеквадратичное отклонение среднего значения по формуле

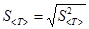
6. Задаваясь вероятностью 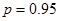и зная число степеней свободы 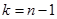, определите по табл.О.1 значение параметра Стьюдента 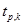. Результат измерения периода колебаний запишите в виде

.
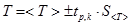