Таблица 0.2: Значения критерия Фишера при надежности в зависимости от числа степеней свободы сравниваемых величин дисперсий.

Дата: 2025-05-25; Просмотры: 4
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

d-1

n-m
3 4 5
2 19.00 19.16 19.25
3 9.55 9.28 9.12
4 6.94 6.59 6.39
5 5.79 5.41 5.19


Критерий для отбрасывания резко выделяющихся результатов измерений

При проведении прямых измерений, как отмечалось ранее, могут присутствовать грубые погрешности (промахи). Действие этих погрешностей проявляется в том, что среди множества 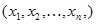полученных измерений величины 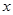встречаются резко выделяющиеся измерения, которые могут быть промахами. Допустим, 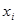является наименьшим значением полученного множества, а 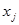- наибольшее значение соответственно. Выдвигается гипотеза о том, что данные измерения 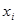и 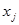принадлежат той же генеральной совокупности распределенной по закону Гаусса, что оставшиеся 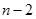значений. Для проверки данной гипотезы используется следующий критерий. Предварительно находят среднее значение и среднеквадратичное отклонение полученной выборки 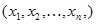. Затем вычисляют следующих два параметра:

.

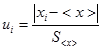
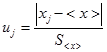Полученные значения сравнивают с табличным значением 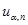, взятым из таблицы 0.3. ( 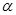- вероятность совершить ошибку при отбрасывании проверяемых измерений, 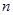-число измерений)

Таблица 0.3:Значения параметра 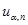, используемого для отбрасывания резко выделяющихся результатов измерений

a=0,10 a=0,05 a=0,01
3 1,15 1,15 1,15
4 1,42 1,46 1,49
5 1,60 1,67 1,75
6 1,73 1,82 1,94
7 1,83 1,94 2,10

Если 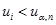, то считается, что результат измерения 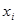принадлежит полученному множеству 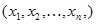. Если 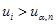, то результат измерения 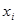считается промахом, и, следовательно, отбрасывается. При этом вероятность совершить ошибку равна заданному значению 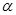. На практике обычно используют значение 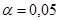. Аналогичные рассуждения проводят и для измерения .

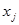Рассмотрим применение данного критерия на следующем примере. Пусть в результате прямых измерений времени падения тела с заданной высоты получены следующие значения: 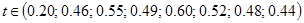. Пусть данные измерения распределены по закону Гаусса. Измерение 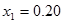, очевидно, резко выделяется среди всех остальных. Проверим гипотезу о том, что данное измерение принадлежит той же генеральной совокупности, что и остальные 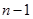измерений.

1. Находим среднее значение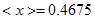

2. Находим дисперсию и среднеквадратичное отклонение времени падения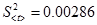

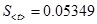
3. Вычислим параметр 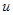для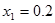

.

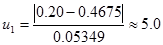4. По таблице 0.3 для вероятности 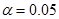находим критическое значение параметра .

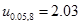5. Сравнивая вычисленное значение параметра 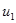с критическим, делаем вывод: поставленную гипотезу о том, что 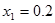принадлежит той же генеральной совокупности, с вероятностью совершить ошибку, равной 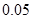, нужно отбросить, т.е. измерение 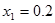выбраковывается из выборки. Затем находим новые значения среднего, дисперсии и среднеквадратичного отклонения.

Критерий для проверки равенства средних двух совокупностей.

Пусть из двух нормально распределенных генеральных совокупностей с неизвестными параметрам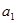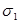и , и 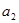, 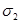получены выборки объемом 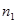и 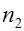.По результатам испытаний подсчитаны оценки параметров 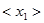, 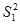; ; 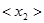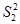. Требуется проверить нулевую гипотезу о равенстве значений этих совокупностей, т.е.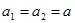

Рассмотрим вначале случай, когда дисперсии генеральных совокупностей равны, т.е. 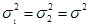. Для проверки поставленной гипотезы 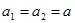вычисляют оценку дисперсии 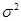по формуле:

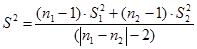(0.25)

и параметр 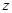по формуле

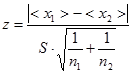. (0.26)

Полученное значение параметра 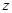сравнивают с значением 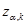, найденным из таблицы 0.4 для заданного значения вероятности совершить ошибку 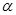и числа степеней свободы .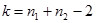