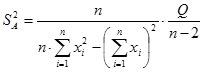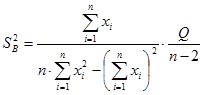Совместные измерения. Метод наименьших квадратов.
Рассмотрим совместные измерения и порядок их обработки на следующем примере. Допустим, величина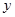 
и величина 
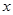связаны линейной зависимостью, т.е.:
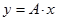(0.10)
Если величины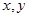 
связанные функционально, измеряются одновременно, то такие измерения называются совместными. Задачей совместных измерений является определение коэффициента 
.
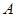Для этого проведем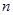 
измерений величин 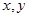, последовательно измеряя их в процессе эксперимента, в результате получим 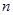пар значений 
, 
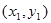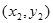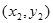,…, . Отметим на плоскости 
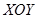экспериментальные точки, соответствующие полученным данным (рис. 0.3).
Вследствие случайных погрешностей полученные экспериментально точки не лежат на одной прямой. Но можно сформулировать критерий для выбора углового коэффициента прямой, в соответствии с которым ошибка измерения этого коэффициента будет минимальной. Этот критерий в математической статистике получил название критерия наименьших квадратов.
Пусть для некоторого определенного значения 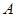прямая 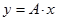пройдет так, как это показано на рис 0.3. Для 
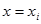ордината 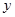при этом равна 
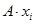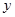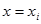, экспериментальное значение для равно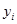 
, т.е. существует отклонение экспериментального значения 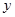от вычисленного значения 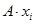. Эти отклонения для каждого измеренного значения величины 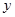могут отличаться как по величине, так и по знаку
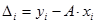(0.11)
Согласно критерию наименьших квадратов, угловой коэффициент прямой 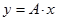должен быть таким, чтобы сумма квадратов отклонений ординат прямой 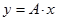при тех же значениях аргумента была минимальной. Это условие метода наименьших квадратов математически записывается так:
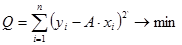(0.12)
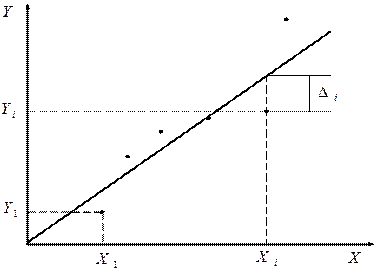
Рисунок 0.3
В выражении (0.12) остаточная сумма квадратов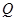 
является функцией неизвестного параметра 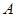. Минимальное значение этой функции достигается тогда, когда ее производная при некотором значении 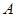равна нулю, т.е.:
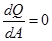(0.13)
Следовательно, взяв от суммы (0.12) производную по параметру 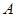и приравняв ее к нулю, получим уравнение:
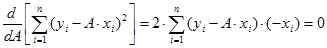(0.14)
Это уравнение линейное относительно А , и из него легко можно получить формулу для нахождения неизвестного параметра :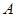
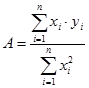(0.15)
Параметр 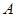является случайной величиной. С помощью методов математической статистики можно найти формулу для дисперсии этого параметра
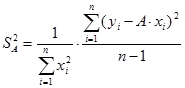(0.16)
Таким образом, метод наименьших квадратов позволяет определить по результатам 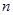совместных измерений, как величину неизвестного параметра 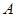, так и его дисперсию 
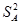. В ряде случаев функциональная зависимость между величинам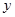и и 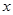может отличаться от простейшей линейной зависимости (0.10).
Часто приходится использовать несколько более сложную зависимость, неизвестными уже могут быть не один, а два параметра, которые в результате совместных измерений необходимо определить. Такой зависимостью, например, является линейная функция вида
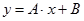(0.17)
Используя метод наименьших квадратов, можно получить расчетные формула для определения параметров 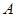и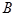 
. Эти формулы записываются в виде
, 
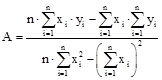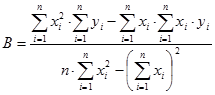(0.18)
Величина дисперсии этих параметров находится по формулам
