Косвенные измерения.
В процессе проведения физических исследований часто приходится вычислять искомую величину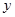 
по результатам прямых измерений, связанных с искомой функциональной зависимостью 
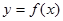. Такие измерения называются косвенными. Причем для такого типа измерений можно предложить порядок их обработки такой же, как для прямых из измерений. Согласно этого методу по результатам прямых измерений 
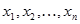находят по формуле 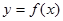значения косвенных измерений 
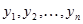, затем по формулам (0.1) и (0.3) вычисляют среднее значение 
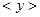дисперсию средних значений косвенных измерений 
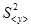. Используя эти величины, записывают доверительный интервал в виде
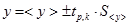
Однако для большого числа измерений данный метод является трудоемким. Поэтому на практике поступают следующим образом.
Среднее значение косвенного измерения 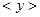находят путем подстановки соответствующих средних значений прямых измерений в следующее равенство 
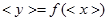. Т.к. при малых значениях 
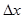приращение 
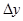пропорционально производной 
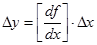, то существует следующая связь среднеквадратичных отклонений 
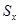и 
:
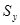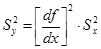(0.7)
Нередко оказывается, что искомая величина является функцией нескольких переменных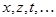 
:
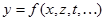(0.8)
В этом случае дисперсия величины 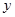определяется по формуле
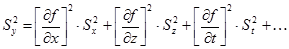(0.9)
где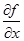 
, 
, 
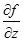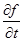- частные производные от функции .
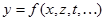Рассмотрим на следующем примере порядок обработки косвенных измерений. Для некоторого бегуна на 100-метровке пятью наблюдателями получены следующие значения времени пробега в секундах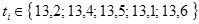 
. Необходимо найти доверительный интервал для величины скорости бегуна.
Первый способ.
1. Предполагая движение бегуна равномерным, находим его скорость
, 
,
, 
,
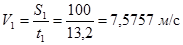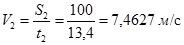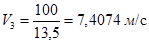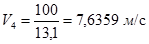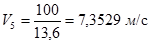
2. Находим среднее значение скорости
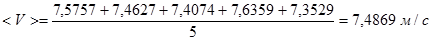
Находим дисперсию среднего значения скорости
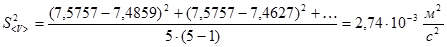
Находим среднеквадратичное отклонение
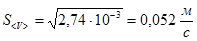
3. Записываем доверительный интервал величины скорости движения бегуна
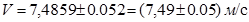
Второй способ.
1. Находит среднее значение времени
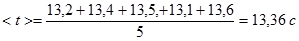
2. Дисперсия и среднеквадратичное отклонение времени
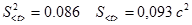
3. Находим среднее значение скорости
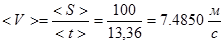
4. Находим формулу для дисперсии скорости
Определяем частные производные
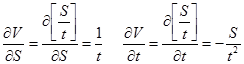
Получаем формулу для дисперсии скорости
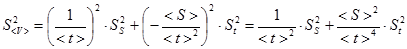
Полагая, что дистанция измерялась лентой с ценой деления 1см, задаем погрешность измерений расстояния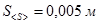 
и вычисляем дисперсию и среднеквадратичное отклонение
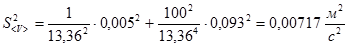
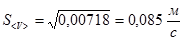
5. Записываем доверительный интервал
.
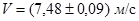Следует обратить внимание на то, что данный доверительный интервал записан без учета параметра Стьюдента, поэтому второй способ обработки результатов косвенных измерений является менее строгим по сравнению с первым. Данный способ обработки результатов косвенных измерений, по сути, является оценочным способом для доверительного интервала.