Лабораторная работа 0-1: обработка результатов физического эксперимента
доц. Миндолин С.Ф.
ЛАБОРАТОРНАЯ РАБОТА 0-1: ОБРАБОТКА РЕЗУЛЬТАТОВ ФИЗИЧЕСКОГО ЭКСПЕРИМЕНТА
Студент группы________________________________________________________________________
Допуск ______________________ Выполнение ____________________Защита __________________________
Цель работы: получение и закрепление навыков обработки результатов прямых, косвенных и совместных измерений.
Основные теоретические сведения
П р ямые измерения
Одной из важнейших задач физического эксперимента являются измерения величин. Процесс измерения состоит в том, что измеряемую величину сравнивают с другой величиной, принятой за эталон. Измерения, в процессе которых искомая величина определяется с помощью специально предназначенного для этого прибора, называются прямыми. Они никогда не бывают абсолютно точными. Всегда возникает разброс результатов измерений, что требует оценки погрешности (ошибки)- обязательного элемента любого эксперимента. Род и причины погрешностей разнообразны и необходимы многочисленные эксперименты, чтобы их систематизировать.
Среди множества ошибок измерений выделим следующие:
Ø систематические погрешности- это погрешности, являющиеся следствием неправильной калибровки (сбитый ноль прибора, тепловое расширение линейки.), ошибочности метода измерений и т.п. При наличии такого типа погрешностей измеренное значение отклоняется от истинного значения в одну и ту же сторону и на одну и туже величину. Повторными измерениями эти ошибки не уменьшаются, однако их можно оценить методом сравнения результатов измерений заданной величины каким-либо прибором с измерениями, полученными исправным прибором (с большей степенью точности).
Ø случайные погрешности вносятся изменчивыми условиями эксперимента, несовершенством органов чувств и трудно учитываемыми условиями эксперимента, ограниченной точностью и т.п. Случайные ошибки уменьшаются с ростом числа измерений пропорционально 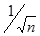 , (где
, (где 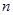 - число измерений в одинаковых условиях) и подчиняются законам теории вероятности и математической статистики. Чаще всего случайные погрешности проявляются в виде разброса (рассеяния) показаний прибора. В результате этого разброса измеряемая величина случайным образом отклоняется от истинного значения в произвольную сторону на произвольную величину.
- число измерений в одинаковых условиях) и подчиняются законам теории вероятности и математической статистики. Чаще всего случайные погрешности проявляются в виде разброса (рассеяния) показаний прибора. В результате этого разброса измеряемая величина случайным образом отклоняется от истинного значения в произвольную сторону на произвольную величину.
Ø промахи- погрешности, чаще всего возникающие вследствие невнимательности человека или недостаточной его квалификации и опыта. Их можно наблюдать, например, при неправильном отсчете измеряемого значения (неправильное определение цены деления прибора). Кроме того, к грубым погрешностям могут привести внезапные сильные внешние влияния на измерительное устройство, повреждения или помехи, которые нельзя считать субъективными.
Ø приборные погрешности- этот тип погрешностей обусловлен тем, что практически любое измерительное устройство обладает ограниченной степенью точности, т.е. ,например, измерительной линейкой с ценой деления 1см нельзя измерить длину стола с точностью до одного миллиметра. Практически для большинства измерительных устройств (за исключением электроизмерительных приборов) в качестве приборной погрешности принимается половина его цены деления.
Ø погрешности округления - связаны с тем, что в расчетах приходится те или иные величины округлять до определенного десятичного разряда.
В методах математической статистики для обработки результатов измерений, в которых присутствуют только случайные погрешности, используется понятие генеральной совокупности значений измеряемой величины и выборки. Например, при измерении времени между двумя событиями или длины предмета, мы, в принципе, можем получить значения, заключенные в интервале 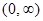 . Множество всех допустимых значений, которые может принимать та или иная величина, называется ее генеральной совокупностью. Производя n измерений, мы получим
. Множество всех допустимых значений, которые может принимать та или иная величина, называется ее генеральной совокупностью. Производя n измерений, мы получим 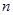 значений измеряемой величины:
значений измеряемой величины: 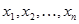 . Данная совокупность значений называется выборкой для величины
. Данная совокупность значений называется выборкой для величины 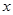 объемом
объемом 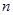 . Очевидно, что выборка переходит в генеральную совокупность, если ее объем, т.е. число измерений
. Очевидно, что выборка переходит в генеральную совокупность, если ее объем, т.е. число измерений 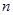 , стремится к бесконечности. Введем понятие среднего значения выборки и ее дисперсии. Средним значением выборки объемом
, стремится к бесконечности. Введем понятие среднего значения выборки и ее дисперсии. Средним значением выборки объемом 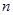 для величины
для величины 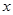 называется величина, вычисляемая из соотношения:
называется величина, вычисляемая из соотношения:
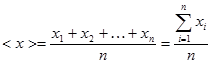 . (0.1)
. (0.1)
Далее введем понятие дисперсии выборки, являющейся мерой отклонений измеренных значений 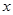 от их среднего значения
от их среднего значения 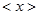 . Дисперсию выборки находят из следующего соотношения
. Дисперсию выборки находят из следующего соотношения
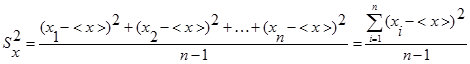 . (0.2)
. (0.2)
Величина, которая является мерой отклонения среднего значения выборки от истинного значения измеряемой величины, называется дисперсией среднего значения. Дисперсия среднего значения обозначается 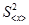 и вычисляется по формуле:
и вычисляется по формуле:
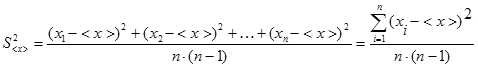 . (0.3)
. (0.3)
Величина 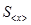 , равная
, равная 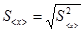 называется среднеквадратичным отклонением среднего значения от истинного значения
называется среднеквадратичным отклонением среднего значения от истинного значения 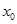 . Очевидно, что среднее значение и дисперсия зависят как от измеренных значений
. Очевидно, что среднее значение и дисперсия зависят как от измеренных значений 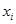 , так и от объема выборки
, так и от объема выборки 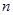 . Причем, при увеличении
. Причем, при увеличении 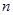 до бесконечности среднее значение и дисперсия выборки стремятся, соответственно, к среднему значению и дисперсии генеральной совокупности. Дисперсию генеральной совокупности обычно обозначают
до бесконечности среднее значение и дисперсия выборки стремятся, соответственно, к среднему значению и дисперсии генеральной совокупности. Дисперсию генеральной совокупности обычно обозначают 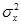 .
.
Результаты измерений величины 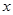 являются случайными числами, поскольку при измерениях присутствуют случайные погрешности измерений. Наиболее часто вероятность получения результата измерений описывается распределением Гаусса. Плотностью распределения величины
являются случайными числами, поскольку при измерениях присутствуют случайные погрешности измерений. Наиболее часто вероятность получения результата измерений описывается распределением Гаусса. Плотностью распределения величины 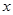 называется функция
называется функция 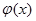 , такая, что вероятность
, такая, что вероятность 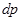 получить измеряемую величину в интервале от
получить измеряемую величину в интервале от 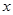 до
до 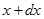 равна
равна 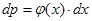 ,
,
где 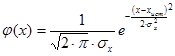 (0.4)
(0.4)
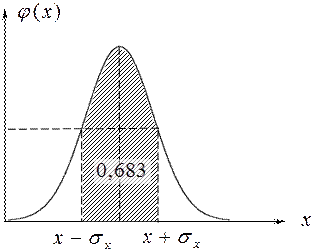 |
На рис 0.1 представлен график функции 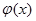 . Важнейшим свойством ее является то, что вероятность получения результата однократного измерения
. Важнейшим свойством ее является то, что вероятность получения результата однократного измерения 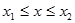 равна площади под кривой в пределах
равна площади под кривой в пределах 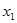 до
до 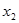 . Например, в пределах от
. Например, в пределах от 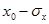 до
до 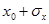 вероятность равна 0.683, в пределах от
вероятность равна 0.683, в пределах от 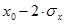 до
до 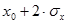 она равна 0.954 и в пределах
она равна 0.954 и в пределах 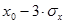 , до
, до 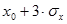 она будет 0.997. Следовательно, из 1000 измерений 683 наиболее вероятно попадут в интервал
она будет 0.997. Следовательно, из 1000 измерений 683 наиболее вероятно попадут в интервал 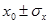 , 954 -в интервал
, 954 -в интервал 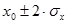 , а 997 соответственно в интервал
, а 997 соответственно в интервал 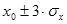 .
.
Рисунок 0.1. График функции распределения Гаусса.
Целью физического эксперимента при проведении прямых измерений является определение интервала, в котором находится истинное значение величины 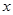 (доверительного интервала). Чтобы записать данный интервал по результатам
(доверительного интервала). Чтобы записать данный интервал по результатам 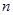 измерений, в которых присутствуют только случайные погрешности, предварительно введем параметр, определяемый по формуле
измерений, в которых присутствуют только случайные погрешности, предварительно введем параметр, определяемый по формуле
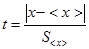 (0.5)
(0.5)
где 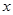 - истинное значение измеряемой величины.
- истинное значение измеряемой величины.
Из данного соотношения видно, что параметр 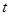 также является величиной случайной, поскольку находится из случайных величин
также является величиной случайной, поскольку находится из случайных величин 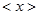 и
и 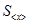 . Следовательно, для всевозможных значений параметра
. Следовательно, для всевозможных значений параметра 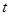 также существует своя функция распределения. Впервые данная зависимость была найдена Стьюдентом и получила название функции распределения Стьюдента, а параметр
также существует своя функция распределения. Впервые данная зависимость была найдена Стьюдентом и получила название функции распределения Стьюдента, а параметр 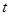 называется параметром Стьюдента. Аналитическое выражения функции распределения параметра Стьюдента имеет следующий вид:
называется параметром Стьюдента. Аналитическое выражения функции распределения параметра Стьюдента имеет следующий вид:
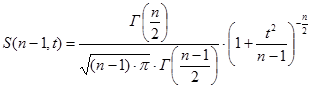 , где
, где 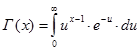 гамма функция.
гамма функция.
График функции распределения параметра Стьюдента представлен на рисунке 0.2. Зная данное распределение и используя следующее равенство 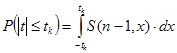 можно вычислить вероятность
можно вычислить вероятность 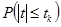 того, что параметр
того, что параметр 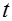 не превосходит значения
не превосходит значения 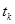 .
.
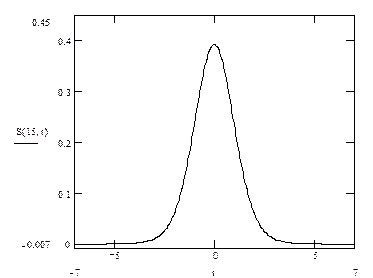
Рисунок 0.2. График функции распределения параметра Стьюдента.
Обычно на практике поступают по иному. Зная количество измерений 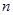 , и задавая вероятность
, и задавая вероятность 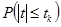 , находят величину параметра
, находят величину параметра 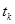 . Значения данного параметра
. Значения данного параметра 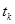 приведены в табл. 0.1. Данные таблицы 0.1 на практике используют следующим образом. Зная объем выборки
приведены в табл. 0.1. Данные таблицы 0.1 на практике используют следующим образом. Зная объем выборки 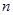 и задавая значение вероятности
и задавая значение вероятности 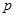 , с помощью табл. 0.1 находят параметр
, с помощью табл. 0.1 находят параметр 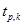 , где
, где 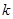 -число степеней свободы (
-число степеней свободы ( 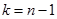 ). После чего из соотношения (0.5) легко получить искомый интервал
). После чего из соотношения (0.5) легко получить искомый интервал
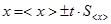 (0.6)
(0.6)
при 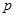 , равном заданному значению, и соответствующем
, равном заданному значению, и соответствующем 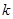 .
.
Данная запись означает то, что истинное значение величины 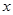 с вероятностью
с вероятностью 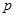 , попадает в указанный интервал. В том случае, если при проведении прямых измерений присутствуют кроме случайных погрешностей и другие виды погрешностей необходимо также учитывать их влияние на искажения полученных результатов. В этом случае дисперсию прямых измерений находят по формуле:
, попадает в указанный интервал. В том случае, если при проведении прямых измерений присутствуют кроме случайных погрешностей и другие виды погрешностей необходимо также учитывать их влияние на искажения полученных результатов. В этом случае дисперсию прямых измерений находят по формуле:
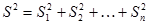 ,
,
где 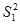 - дисперсия измерений от случайных погрешностей,
- дисперсия измерений от случайных погрешностей, 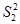 - дисперсия измерений от приборных погрешностей и т.д. Следует заметить, что из полученных прямых измерений оценить систематическую погрешность не представляется возможным.
- дисперсия измерений от приборных погрешностей и т.д. Следует заметить, что из полученных прямых измерений оценить систематическую погрешность не представляется возможным.
Рассмотрим пример обработки результатов прямых измерений. Допустим, в результате пяти измерений получены значения: 6,7,6,5,6. Порядок обработки полученных измерений заключается в следующем.
1. Находим среднее значение измерений по формуле (0.1)
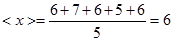 .
.
2. Дисперсию среднего значения находим по формуле (0.3.)
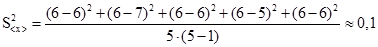
Тогда среднеквадратичное отклонение среднего значения равно
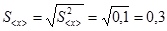 .
.
3. Для вероятности 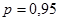 и числа измерений
и числа измерений 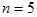 , находим значение параметра
, находим значение параметра 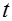 из табл. 0.1: (
из табл. 0.1: ( 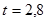 .)
.)
4. Окончательный результат записываем в виде
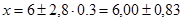 при
при 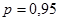 .
.
Таблица 0.1
Значение параметра Стьюдента в зависимости от вероятности 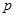 и числа степеней свободы
и числа степеней свободы 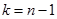 .
.
| k | Вероятность p | |||||||
| 0,6 | 0,7 | 0,8 | 0,9 | 0,95 | 0,98 | 0,99 | 0,999 | |
| 1 | 1,38 | 2,0 | 31 | 6,3 | 12,7 | 31,8 | 63,7 | 636,6 |
| 2 | 1,06 | 1,3 | 1,9 | 2,9 | 4,3 | 7,0 | 9,9 | 31,2 |
| 3 | 0,98 | 1,3 | 1,6 | 2,4 | 3,2 | 4,5 | 5,8 | 12,9 |
| 4 | 0,94 | 1,2 | 1,5 | 2,1 | 2,8 | 3,7 | 4,6 | 8,8 |
| 5 | 0,92 | 1,2 | 1,5 | 2,0 | 2,6 | 3,4 | 4,0 | 6,9 |
| 6 | 0,90 | 1,1 | 1,4 | 1,9 | 2,4 | 3,1 | 3,7 | 6,0 |
| 7 | 0,90 | 1,1 | 1,4 | 1,9 | 2,4 | 3,0 | 3,5 | 5,4 |
| 8 | 0,90 | 1,1 | 1,4 | 1,9 | 2,3 | 2,9 | 3,4 | 5,0 |








