Магнитное поле в кабеле

Дата: 2025-04-30; Просмотры: 2
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

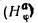
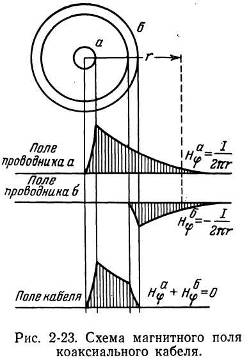
В кабеле под нагрузкой по токопроводящим жилам проходит электрический ток и вызывает вокруг жил магнитное поле, харак­теризующееся величиной напряженности H. На рис. 2–23 представ­лены кривые напряженности магнитного поля внутреннего

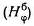
и внешнего

проводников коаксиального кабеля и результирующего магнитного поля. Во внутреннем проводнике коаксиального кабеля магнитное поле

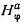
возрастает от центра к его поверхности, а вне его уменьшается по закону

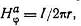
где r — радиус внутреннего проводника. Внутри внешнего проводника (цилиндрической формы) магнитное поле отсутствует, а вне его выражается уравнением:

 

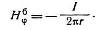
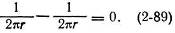
Токи во внутреннем и внешнем проводниках кабеля равны по величине, но обратны по знаку. Магнитные поля внутреннего и внешнего про­водников в любой точке про­странства вне кабеля также будут равны по величине и противоположно направлены. Результирующее поле вне ка­беля

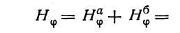
Линии магнитной индук­ции коаксиального кабеля рас­полагаются в виде концентри­ческих окружностей внутри него. Вне кабеля магнитное поле отсутствует.

Линии магнитной индукции двухжильного (симметричного) ка­беля располагаются эксцентричными по отношению к жиле окруж­ностями (рис. 2-17), распространяясь на значительное от них рас­стояние. Из-за наличия внешнего поля возникают потери в соседних цепях, металлических оболочках и в броне кабеля.

Магнитное поле в кабеле вызывает увеличение электрического сопротивления токопроводящих жил кабеля за счет поверхностного эффекта, появление электродинамических усилий, потерь в метал­лических оболочках кабеля и мешающих влияний в кабелях связи.

РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНОЙ ЭНЕРГИИ В КАБЕЛЕ

Совокупность электрического и магнитного полей, распростра­няющихся вдоль линии с определенной скоростью, называют элек­тромагнитной волной. На всем пути, проходимом электромагнитной волной, энергия электрического поля Wэ равна энергии магнитного поля WM. Энергия магнитного поля может переходить в энергию электрического поля и наоборот. При передаче по цепи энергии вы­сокочастотных колебаний плотность тока увеличивается к поверхно­сти токопроводящей жилы кабеля, причем чем выше частота, тем сильнее эффект вытеснения тока на поверхность жилы. Электромаг­нитная энергия при передаче по цепи сосредоточивается в основном в изоляции, окружающей жилу, поэтому при передаче сигналов свя­зи по жилам кабеля носителем высокочастотной магнитной энергии являются не жилы кабелей, а окружающая их среда. Жилы кабеля лишь задают направление движения энергии. Благодаря жилам ка­беля электромагнитная энергия не рассеивается во все стороны, а движется вдоль линии.

Электромагнитная волна состоит из волны напряжения и волны тока. Между ними в любой точке цепи существует определенное со­отношение, зависящее от свойств цепи и имеющее размерность со­противления (ом), называемое волновым сопротивлением

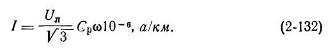
Распространение электромагнитной энергии вдоль однородной кабельной линии с согласованными нагрузками характеризуется уравнениями:

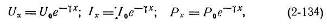
где U0, I0 и Р0 — напряжение, ток и мощность в начале цепи; Ux, Ix и Px — напряжение, ток и мощность в любой точке цепи на рас­стоянии х от ее начала; γ — коэффициент распространения.

Между напряжением, током и мощностью в начале (0) и конце кабельной линии (l) существует следующая зависимость:

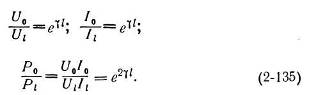
При согласованной нагрузке Zе

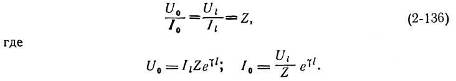
При несогласованной нагрузке (ZH), когда цепь изолирована на конце (ZH = ∞), или цепь замкнута накоротко (ZH = 0), электромаг­нитная энергия, дойдя до конца линии, полностью отразится и не будет воспринята приемником. В случае, когда цепь нагружена на любое сопротивление, отличное от Zc, за счет несогласованности появятся отраженные волны и лишь часть энергии поступит в при­емник.

Скорость распространения электромагнитных волн по кабелю определяется частотой тока и параметрами цепи. При передаче по кабельной цепи электромагнитная энергия уменьшается (затухает) по амплитуде и изменяется по фазе. Явление затухания обусловлено тепловыми потерями энергии в токопроводящих жилах, потерями в изоляции на диэлектрическую поляризацию, дипольными потерями, токами утечки и т. д.

Качество передачи по кабельным линиям связи и их электриче­ские свойства характеризуются первичными параметрами кабеля: активным сопротивлением токопроводящих жил R, индуктивностью L, емкостью С и проводимостью изоляции G, относимыми к единице длины. Эти параметры не зависят от напряжения и передаваемого тока, а зависят от конструкций кабеля и частоты используемого тока.

Волновое (характеристическое) сопротивление Z и коэффициент распространения γ являются вторичными параметрами линии, широ­ко используемыми для оценки эксплуатационно-технических качеств линии связи.

6 вопрос.

Ротор вектора.

Ро́тор, или вихрь — векторный дифференциальный оператор над векторным полем.

Ротором вектора 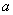называется вектор

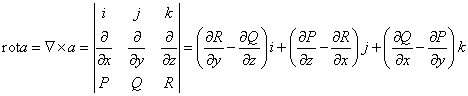
Таким образом, можно сказать, что ротор вектора 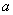равен векторному произведению символического вектора (оператора Гамильтона) на вектор .

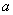Теорема Стокса — одна из основных теорем дифференциальной геометрии и математического анализа об интегрировании дифференциальных форм, которая обобщает несколько теорем анализа. Названа в честь Дж. Г. Стокса.

Пусть на ориентируемом многообразии 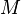размерности 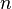заданы ориентируемое 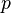-мерное подмногообразие 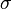и дифференциальная форма 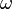степени 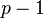класса 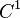( 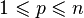). Тогда, если граница подмногообразия 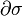положительно ориентирована, то

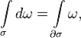
где 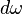обозначает внешний дифференциал формы .

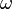Теорема распространяется на линейные комбинации подмногообразий одной размерности, так называемые цепи. В этом случае формула Стокса реализует двойственность между когомологией де Рама и гомологией циклов многообразия .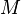

Теорема Стокса

Циркуляция вектора по замкнутому контуру, являющегося границей некоторой поверхности, равна потоку ротора этого вектора через эту поверхность:

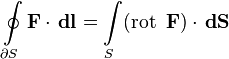
Частный случай теоремы Стокса для плоской поверхности - содержание теоремы Грина.

7 вопрос.