Метод электрических изображений, изображение относительно плоскости

Дата: 2025-04-30; Просмотры: 2
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

Теорема единственности в электростатике обосновывает «метод изображений». Он помогает решать задачи с участием точечного заряда. Задача состоит в следующем: имеется замкнутая область пространства с заданными распределением зарядов и граничными условиями (например, потенциал на границе). Нужно найти электрическое поле (потенциал, а из него напряженность) в этой области. Решение «методом изображений» состоит в подборе фиктивных зарядов вне рассматриваемой области, таких, что их совместное с реальными зарядами поле обеспечивает заданные граничные условия (потенциал на границе). Поскольку внутри области заряды не изменились, найденное поле удовлетворяет уравнению Пуассона (является его решением). Выполняются также граничные условия. По теореме единственности других решений нет. Примеры «методы изображений» приведены далее.

Сила, действующая на заряд +q со стороны плоскости:

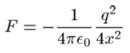
Напряженность поля вблизи плоскости:

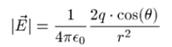
Плотность индуцированного на плоскости заряда:

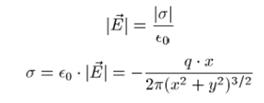
4 вопрос.

Электри́ческий ток — направленное (упорядоченное) движение заряженных частиц. Такими частицами могут являться: в металлах — электроны, в электролитах — ионы (катионы и анионы), в газах — ионы и электроны, в вакууме при определенных условиях — электроны, в полупроводниках — электроны и дырки (электронно-дырочная проводимость). Иногда электрическим током называют также ток смещения, возникающий в результате изменения во времени электрического поля[4].

Электрический ток имеет следующие проявления:

· нагревание проводников (не происходит в сверхпроводниках);

· изменение химического состава проводников (наблюдается преимущественно в электролитах);

· создание магнитного поля (проявляется у всех без исключения проводников)[3].

Пло́тность то́ка — векторная физическая величина, имеющая смысл силы тока, протекающего через элемент поверхности единичнойплощади[1]. Например, при равномерном распределении плотности тока и всюду ортогональности её плоскости сечения, через которое вычисляется или измеряется ток, величина вектора плотности тока:

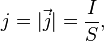
где I — сила тока через поперечное сечение проводника площадью S.

Сторонние силы.

Сторонняя электродвижущая сила совершает положительную работу по перемещению положительного заряда в сторону возрастания потенциала, т.е. против сил электростатического поля (вследствие сопротивления потенциал электростатического поля понижается, положительный заряд двигается от большего потенциала к меньшему => должны существовать участки, на которых “+” заряд движется от меньшего потенциала к большему ).

Сторонняя сила не может иметь электростатического происхождения т.к. электростатическое поле — потенциальное и А по замкнутому пути =0 и ток не мог бы существовать, т.к. он должен совершать работу для преодоления сопротивления проводника.

Физическая природа сторонних сил весьма различна:

Они могут быть обусловлены:

а) химической, физической неоднородностью проводника при соприкосновении разнородных проводников (гальванические элементы; аккумуляторы—возникает контактная разность потенциалов при контакте твёрдого тела и жидкости)

б) физическая неоднородность при соприкосновении проводников различной температуры ( термоэлементы)

в) механические происхождения

г) электрическое происхождение — сила действует на заряд в электростатическом поле , возникающем по закону электромагнитной индукции.

Электри́ческая мо́щность — физическая величина, характеризующая скорость передачи или преобразования электрической энергии. Если сила перемещает тело на некоторое расстояние, то она совершает над телом работу.

Работа W есть произведение силы F на перемещение s.

1. W= F·s

5 вопрос.

Магнетизм.
Это форма взаимодействия движущихся электрических зарядов, осуществляемая на расстоянии посредством магнитного поля. Наряду с электричеством, магнетизм — одно из проявлений электромагнитного взаимодействия.

Сила Лоренца.

Сила, с которой электромагнитное поле действует на точечную частицу. Иногда силой Лоренца называют силу, действующую на движущийся со скоростью V заряд g лишь со стороны магнитного поля. Полная сила со стороны электромагнитного поляе - это сила со стороны электрического E и магнитного B полей. Выражается в СИ как:

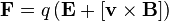
Сила Ампера.

Сила, действующая на проводник с током в магнитном поле, называется силой Ампера.
Сила действия однородного маг­нитного поля на проводник с током прямо пропорциональна силе тока, длине проводника, модулю вектора индукции магнитного поля, синусу угла между вектором индукции магнитного поля и проводником:

 

 

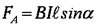
Законы магнетизма


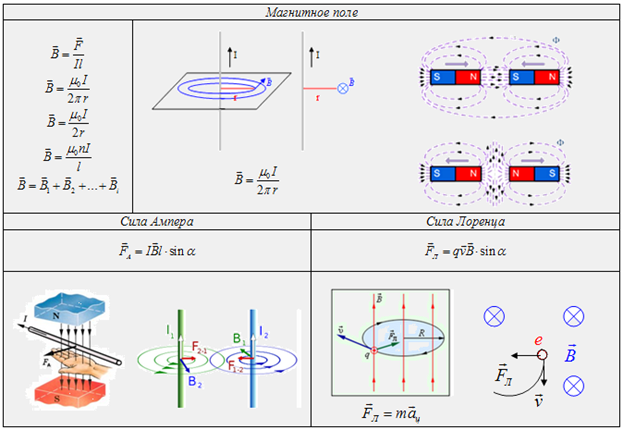
Основные законы электромагнетизма.

Первый закон электромагнетизма.

Для любого замкнутого контура индуцированная электродвижущая сила (ЭДС) равна скорости изменения магнитного потока, проходящего через этот контур.
или Генерируемая ЭДС пропорциональна скорости изменения магнитного потока.

Индуктивность( коэффициент самоиндукции ) — коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током через поверхность, краем которой является этот контур.

Колебательный контур.
Представляет собой электрическую цепь, содержащую соединённые катушку индуктивности и конденсатор. В такой цепи могут возбуждаться колебания тока и напряжения.
Колебательный контур — простейшая система, в которой могут происходить свободные электромагнитные колебания

 

Законы электромагнетизма

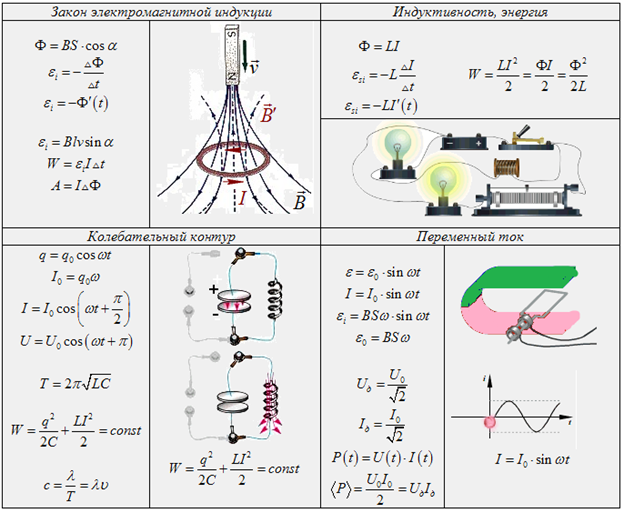
Магнитное поле постоянного тока

Магнитное поле постоянного тока не изменяется во времени и является частным случаем электромагнитного поля. Магнитное поле создается электрическими токами. Магнитное поле может быть обнаружено силовым воздействием на постоянный магнит или на проводник с постоянным током.

Закон непрерывности магнитного потока

Поток вектора магнитной индукции через любую замкнутую поверхность равен нулю

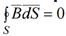
Линии векторов В и Н всегда замкнуты и не имеют конца.

Закон полного тока. В интегральной форме

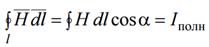
Линейный интеграл от напряженности магнитного поля вдоль любого замкнутого контура равен полному току, охватываемому этим контуром

В дифференциальной форме 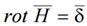т.е. во всех точках пространства, где вектор вектор плотности тока не равен нулю магнитное поле является вихревым.

Для расчета магнитного поля используется векторный потенциал А, удовлетворяющий условиям 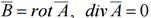и уравнению Пуассона 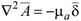. теорема о циркуляции напряженности магнитного поля.

Циркуляция магнитного поля постоянных токов по всякому замкнутому контуру пропорциональна сумме сил токов, пронизывающих контур циркуляции.

В математической формулировке для магнитостатики теорема имеет[2]следующий вид[1][3]:

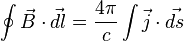
Здесь 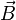— вектор магнитной индукции, 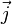— плотность тока; интегрирование слева производится по произвольному замкнутому контуру, справа — по произвольной поверхности, натянутой на этот контур. Данная форма носит название интегральной, поскольку в явном виде содержит интегрирование. Теорема может быть также представлена в дифференциальной форме[4]:

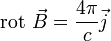
Эквивалентность интегральной и дифференциальной форм следует из теоремы Стокса[5].

Приведённая выше форма справедлива для вакуума. В случае применения её в среде (веществе), она будет корректна только в случае, если под j понимать вообще все токи, то есть учитывать и «микроскопические» токи, текущие в веществе, включая «микроскопические» токи, текущие в областях размерами порядка размера молекулы (см. диамагнетики) и магнитные моменты микрочастиц (см.например ферромагнетики).

Поэтому в веществе, если не пренебрегать его магнитными свойствами, часто удобно из полного тока выделить ток намагничения (см. связанные токи), выразив его через величину намагниченности 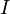и введя вектор напряжённости магнитного поля

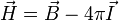
Тогда теорема о циркуляции запишется в форме[6]

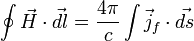
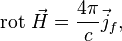
где под 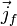(в отличие от 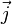в формуле выше) имеются в виду т. н. свободные токи, в которых ток намагничения исключен (что бывает удобно практически, поскольку 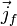— это обычно уже в сущности макроскопические токи, которые не связаны с намагничением вещества и которые в принципе нетрудно непосредственно измерить)[7].

В динамическом случае — то есть в общем случае классической электродинамики — когда поля меняются во времени (а в средах при этом меняется и их поляризация) — и речь тогда идет об обобщенной теореме, включающей 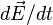, — всё сказанное выше относится и к микроскопическим токам, связанным с изменениями поляризации диэлектрика. Эта часть токов тогда учитывается в члене .

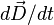Основным фундаментальным обобщением[8] теоремы является четвёртое уравнение Максвелла. В интегральной форме оно является прямым обобщением на динамический случай магнитостатической формулы, приведённой выше. Для вакуума:

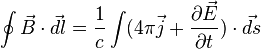
для среды]:

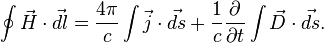
(Как видим, формулы отличаются от приведенных выше только одним добавочным членом со скоростью изменения электрического поля в правой части).

Дифференциальная форма этого уравнения:

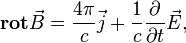
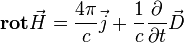
(в гауссовой системе, для вакуума и среды соответственно) — также можно при желании считать вариантом обобщения теоремы о циркуляции магнитного поля, поскольку она, конечно, тесно связана с интегральной.

Коаксиальный кабель (от лат. co — совместно и axis — ось, то есть «соосный»), также известный как коаксиал (от англ. coaxial), — электрический кабель, состоящий из расположенных соосно центрального проводника и экрана. Обычно служит для передачи высокочастотных сигналов. Изобретён и запатентован в 1880 году британским физиком Оливером Хэвисайдом.