Взаимная индукция, трансформатор
Цель работы. Измерить индуктивность магнитосвязанных соленоидов. Изучить явление взаимной индукции, определить коэффициент трансформации трансформатора.
Краткое теоретическое введение
1.Магнитосвязанные соленоиды.
Рассмотрим два соленоида с индуктивностями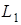 
и 
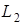. Поставим вопрос, чему равна индуктивность системы, состоящей из этих последовательно соединенных соленоидов, если они расположены так, что магнитные поля перекрываются.
Индуктивность системы определяется потокосцеплением, т.е. общим потоком через все витки:
,
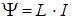где I – сила тока в соленоидах.
Суммарный магнитный поток равен алгебраической сумме потоков, пронизывающих все витки соленоида. Все витки первого соленоида пронизываются собственным потоком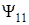 
и потоком 
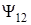, созданным вторым соленоидом. Второй соленоид пронизывается также собственным потоком 
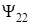и потоком 
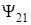, созданным первым соленоидом. Таким образом,
.
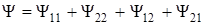Собственные потоки всегда положительны:
, 
.
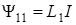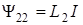«Чужие» потоки могут быть как положительными, так и отрицательными в зависимости от направления вектора магнитной индукции поля, созданного одним соленоидом в витках другого. При этом знаки магнитных потоков 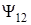и 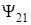всегда совпадают. Так как соленоиды соединены последовательно, то
,
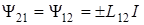где коэффициент пропорциональности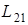 
, L21 называется взаимной индуктивностью второго и первого контуров.
Смысл знаков определяется характером соединения и расположения соленоидов. Если магнитные поля соленоидов сонаправлены, то «чужие» потоки положительны: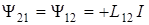 
если поля направлены навстречу друг другу, то – отрицательны: 
.
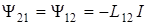Учитывая сказанное, для индуктивности системы двух соленоидов получим:
,
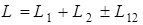где знак плюс соответствует случаю сонаправленных полей, а минус – полям, направленным навстречу друг другу.
2. Взаимная индукция. Трансформатор
Явление взаимной индукции заключается в наведении ЭДС индукции в проводнике, находящемся вблизи цепи переменного тока.
Из закона электромагнитной индукции Фарадея следует, что ЭДС взаимной индукции равна
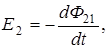(1)
где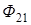 
- магнитный поток через поверхность, ограниченную вторым контуром, обусловленный магнитным полем тока 
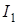, протекающего в первом контуре (Рис. 1).
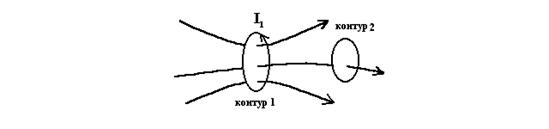
Рис. 1.
Чем больше сила тока 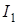в первом контуре, тем больше магнитный поток 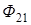, обусловленный этим током. Поэтому, так же как и при самоиндукции, этот магнитный поток пропорционален силе тока:
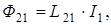(2)
где, как говорилось выше, коэффициент пропорциональности 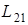называется взаимной индуктивностью (статической взаимной индуктивностью) второго и первого контуров. Этот коэффициент зависит от геометрических размеров, формы, количества витков, взаимного расположения первого и второго контура, от магнитной проницаемости среды, в которой они находятся.
Если источник тока отключить от первого контура и подключить ко второму, создав ток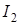 
, то для магнитного потока через площадь первого контура 
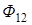можно записать аналогичную формулу:
.
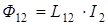Пусть контуры находятся в неферромагнитной среде, тогда, как можно показать, для них выполняется, так называемая, теорема взаимности, согласно которой коэффициенты взаимной индуктивности равны друг другу численно и имеют одинаковые знаки:
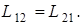
Если же среда ферромагнитная, причем режим перемагничивания среды выходит за пределы обратимого процесса, то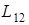 
и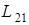 
зависят не только от вышеперечисленных параметров, но и от величины токов в контурах. В этом случае теорема взаимности не выполняется.
Заменив в законе Фарадея (1) магнитный поток его выражением (2) и полагая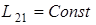 
, получим
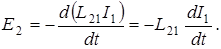(3)
Если первый и второй контуры находятся в ферромагнитной среде, то можно пользоваться формулой, по форме аналогичной формуле (3):
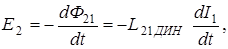(4)
где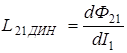 
- так называемая динамическая взаимная индуктивность второго и первого контуров.