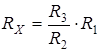Контрольные вопросы
1. В чем заключается цель настоящей работы?
2. Как найти точки с одинаковым значением потенциала?
3. Как определить значение потенциала на эквипотенциальной поверхности, относительно какого тела он определяерся?
4. Что такое напряженность и потенциал электростатического поля?
5. Какова связь напряженности с разностью потенциалов?
6. Каково взаимное влияние проводящего тела и электростатического поля?
7. Каково взаимное влияние диэлектрического тела и электростатического поля?
8. Сформулируйте теорему Гаусса для вектора напряженности электростатического поля в вакууме. Объясните, для чего и как она применяется.
Список литературы
1. Калашников С.Г. Электричество.- М.: Наука, 1974
2. Савельев И.В. Курс общей физики. - М.: Наука, 1982.- Т.2 и последующие издания этого курса.
3. Барановский С.Н., Березиков Д.Д., Погорельский А.М., Потапов Н.П., Юровская С.М. Механика. Электричество. Магнетизм.- Новосибирск, 1995
Лабораторная работа № 12
МЕТОДЫ ЭЛЕКТРИЧЕСКИХ ИЗМЕРЕНИЙ
Цель работы. Овладеть методами измерения электрических величин с помощью амперметра, вольтметра, осциллографа.
Измерение сопротивления с помощью вольтметра и амперметра
Экспериментально установлена зависимость силы тока I, текущего по металлическому проводнику, от напряжения U на концах проводника
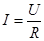- закон Ома для участка цепи,
где R - электрическое сопротивление проводника, имеющее единицу измерения 1 0м - сопротивление такого проводника, в котором при напряжении 1В течет постоянный ток силой 1А.
Используя рабочую формулу 
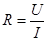, можно определить величину сопротивления R для нескольких значений напряжения U на концах проводника.
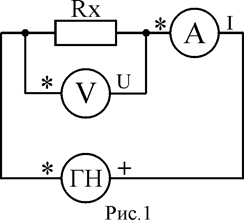
Измерения U и I проводятся с помощью вольтметра и амперметра по схеме рисунка 1.
Для достоверного определения RX необходимо, чтобы сопротивление вольтметра RV>>RX.
Измерения R проводятся косвенным методом при различных значениях напряжения U генератора напряжения, что позволяет определить R для нескольких измерений и рассчитать величину погрешности.
Измерение неизвестного сопротивления
при помощи моста постоянного тока
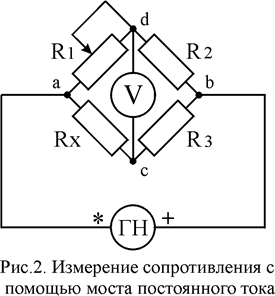
Рассмотрим схему моста постоянного тока, представленную на рис.2.
Rx - неизвестное сопротивление, R1 - переменное сопротивление, R2 и R3 - известные сопротивления. Во входную диагональ моста (a b) включается питание моста, а в выходную (с d) - индикатор равновесия (вольтметр, осциллограф или миллиамперметр). Если разность потенциалов jс - jd равна 0, мост находится в равновесии. При подключении измерительного прибора к точкам с и d диагональ моста (с d) замыкается, сила тока, равная 0, обеспечивается изменением переменного сопротивления R1.
Для того, чтобы мост находился в равновесии, необходимо, чтобы выполнялись следующие соотношения
U ac = U ad (1)
U cb = U db (2)
При равновесии моста на участке моста a c b протекает ток Ix , а на участке a d b - ток I1, отсюда
U ac = Ix × Rx (3)
Uad = I1× R1 (4)
U cb = Ix × R3 (5)
U db = I1× R2 (6)
Процесс измерения состоит в том, что при установленном отношении плеч моста R3/ R2 добиваются равновесия моста, изменяя переменное сопротивление R1.
Формулу для измеряемого сопротивления Rx получим из (3) - (6), используя (1), (2):
Ix × Rx = I1 × R1 (7)
Ix × R3 = I1 × R2 (8)
Разделив (7) на (8), получим для измеряемого сопротивления:
