Вопрос 43. Вариационная задача с подвижным концом .
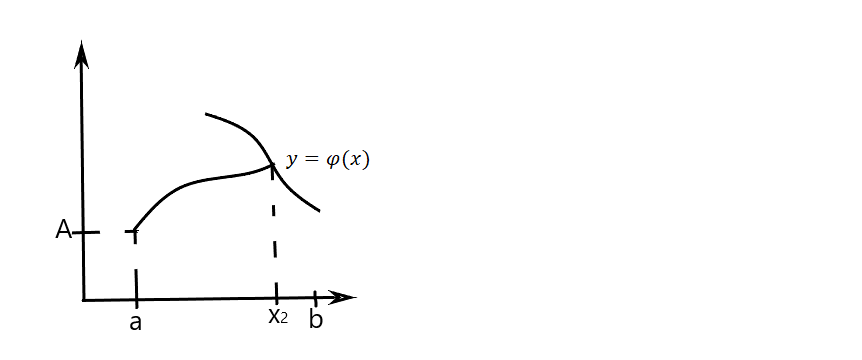
Ставится задача нахождения экстремума функционала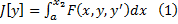 
при условии, что левый конец закреплен 
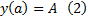а правый подвижен, причем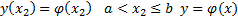 
Теор. Если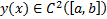 
реализует экстремум функционала (1) с закрепленным левым концом (2) и подвижным правым 
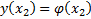и выполняются условия :
1) 
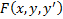непрерывна с элементами до 2-го порядка включительно
2) 
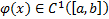, тогда
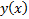является решением уравнения Эйлера для функционала (1) : 
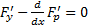, удовлетворяющим условиям (2), (3) и кроме того, на правом конце для него выполняется условие транверсальности :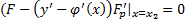 
#без доказательства#
Замеч. Если закреплен правый конец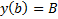 
, а левый движется по закону 
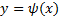, т.е. 
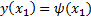, тогда на
левом конце должно выполнятся условие трансверсальности :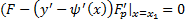 
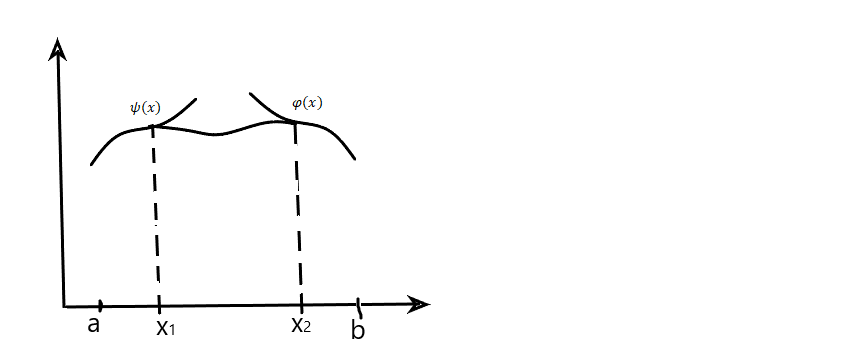
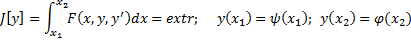
Тогда на обоих концах должно выполнятся условие трансверсальности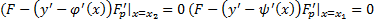 
Замеч. В случае свободного конца ( правый закреплен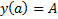 
, левый свободный 
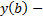любое ) условие трансверсальности приобретает вид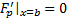 
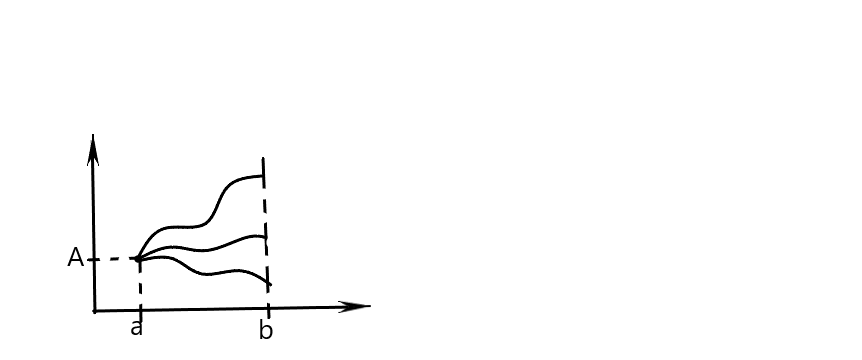
Пример 1. Найти условие трансверсальности для функционала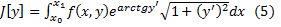 
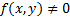
Решение. Пусть левый конец экстремали закреплен в точке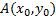 
, а правый конец 
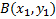может перемещаться по кривой 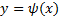. Тогда получим 
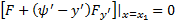. В нашем случае 
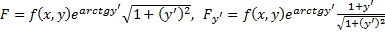. Условие трансверсальности запишется так : 
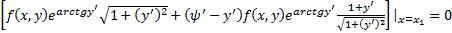. Отсюда в силу условия 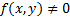, получаем 
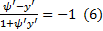. Геометрически условие(6) означает, что экстремали 
должны пересекать кривую , по которой скользит граничная точка по углом 
.
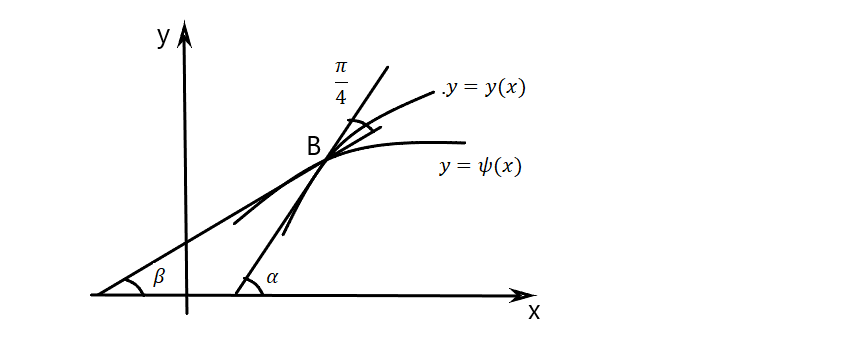В самом деле, соотношение (6) можно представить так: положим, что касательная к экстремали в точке , лежащей на кривой , пересекает ось Ox под углом 
а касательная к заданной кривой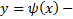 
под углом 
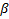. Тогда 
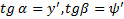и левая часть формулы (6) дает 
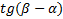, но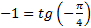 
, поэтому 
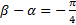, откуда 
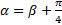, откуда 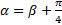, что и требовалось показать.
Пример 2.Найти минимальное расстояние между параболой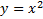 
и прямой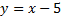 
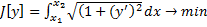
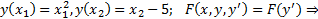экстремали прямые линии вида 
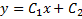. Выбираем экстр. удов. гранич. условиям: 
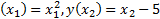и условиям трансверсальности: 
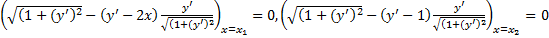. Поскольку 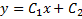, то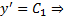 
условие трансверсальности приобретает следующий вид :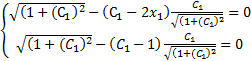 
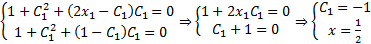. Теперь используем граничные условия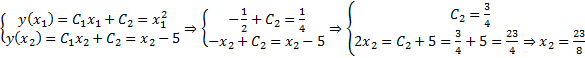 
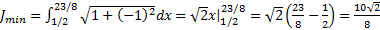
Комплексозначные решения ОСЛОДУ с действительными коэффициентами.
Если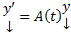 
имеет комплексозначные коэффициенты, все свойства решений, матрицы решений и ОВ сохраняются.
Рассмотрим теперь систему с действительными коэффициентами. Она может обладать комплексозначными решениями.
Теор. Если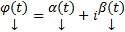 
, где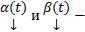 
столбцы действительных функций является решениемм ОСЛОДУ с действительными коэффициентами 
. 
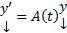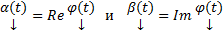также является решениями этой ОСЛОДУ
Док-во: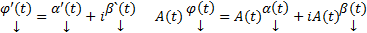 
Приравнивая действительные и мнимые части 
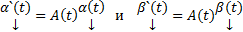. Более того, поскольку 
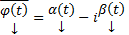является ЛК решений, 
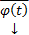также является решением этой системы.
Все ТСЕ
Теор1.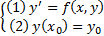 
Теор2.(ТСЕ решение ЗК уравнения 1-го порядка, не разрешенных относительно производной)
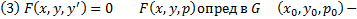некоторая точка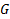 
Пусть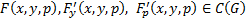 
. Тогда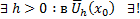 
Решение уравнения (3) н.у. (2) при этом дополнительно выполняется, что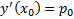 
Теор3. ТСЕ решние ЗК для нормальной СОДУ
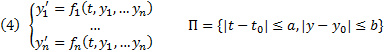Если 
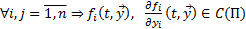, то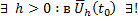 
Решение нормальной СОДУ (4) удовлетворяющее н.у.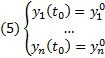 
Теор4. ТСЕ решения ЗК для нормальной СЛОДУ
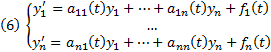Если 
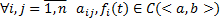, то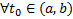 
и любого набора начальных условий (5) 
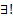Решение ЗК (6) (5) на всем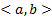 
Теор5. ТСЕ решения ЗК для уравнения n-го порядка, разрешенного относительно старшей производной
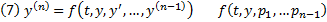определена в G 
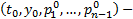внутренняя точка в G. Если 
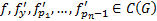, то 
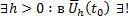Решение уравнения (7), удовлетворяющее начальным условиям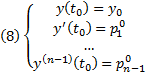 
Теор6. ТСЕ для ЛОДУ n-го порядка
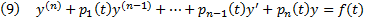. Если 
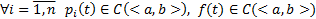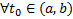, то и любого набора начальных условий (8) Решение ЗК (9) (8) на всем