Вопрос 41. Условный экстремум .
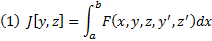
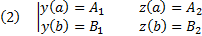
Задача. Найти экстремум функционала (1) с закрытыми концами (2) при наличии дополнительных условий
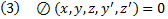
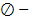заданная функция своих переменных
Эта задача называется задачей нахождения условного экстремума с неголономной связью
Теор. Если пара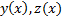 
реализует экстремум функционала (1) с закрытыми концами (2) при наличии неголономной связи (3) и выполняются условия :
1) 
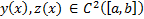
2) 
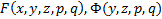непрерывны со своими частичными производными до 2-го порядка включительно
3) 
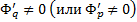
то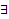 
дифференцируемая функция 
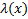, такая что 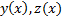является решением краевой задачи Эйлера для функционала 
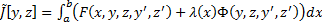с дополнительными условиями (3), т.е.
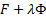
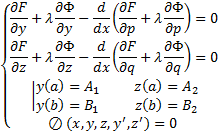
Без док-ва.
Рассмотрим так называемую изопериметрическую задачу. Найти экстремум функционала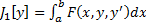 
с закрытыми концами 
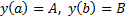, при условии, что функционал 
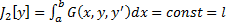(имеет заданное значение)
Часто в качестве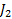 
берут функционал 
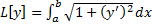, который задает длину кривой, соединяющей 
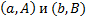, т.е. длина кривой фиксированна (т.е. ищется экстремум функционала 
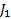при условии постоянства длины кривой)
Сведем эту задачу к задаче с неголономной связью. Рассмотрим функцию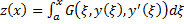 
. Тогда 
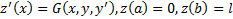. Таким образом, имеем следующую вариационную задачу : Найти экстремум функционала 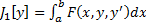с закрытыми концами 
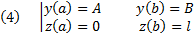при наличии связи (неголономной) 
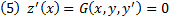. Тогда, если 
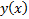реализует экстремум функционала 
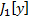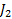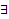и не является экстремалью функционала , то число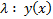 
является решением КЗ Эйлера для функционала 
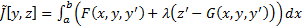, т.е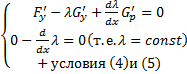 
Пример . Задача Дидоны.
Огородить максимальную площадь веревкой длины 2l с концами, закрепленными на расстоянии 2a друг от друга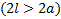 
. 
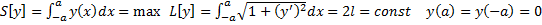. Рассмотрим 
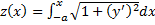. Тогда 
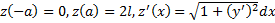имеем вариационную задачу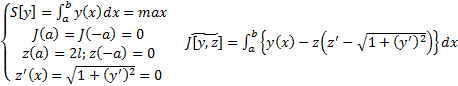 
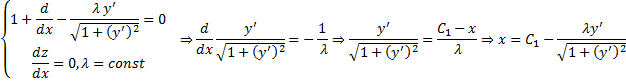
Решаем это уравнение методом введения параметра
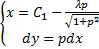
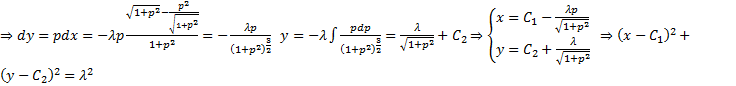Из краевых условий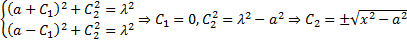 
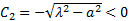. Рассмотрим этот случай: при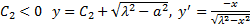 
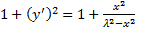
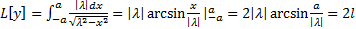
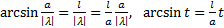
решение при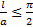 
, т.е. при 
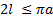. Если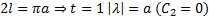 
Вопрос 42.
Рассмотрим теперь задачу нахождения экстремума функционала (1) с закрытыми концами (2) при наличии голономной связи :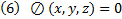 
. В этом случае теоремой функционала с неголономной связью воспользоваться нельзя, поскольку 
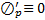и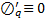 
. Кроме того, из-за наличия голономной связи (6) краевого условия (2) становится зависимым, т.е. числа 
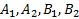не могут быть какими угодно, а должны удовлетворять условиям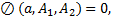 
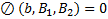т.е. только одно число из каждой пары 
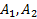и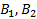 
выбираются свободно.
Теор. Пусть пара 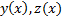реализует экстремум функционала (1) с голономной связью (6) и краевыми условиями (2) (которые тоже удовлетворяют этой связи), причем :
1)
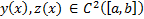
2) 
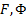непрерывны со своими частичными производными до 2-го порядка включительно
3) 
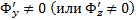
то 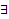непрерывная функция 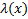, такая что 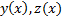является решением краевой задачи Эйлера для функционала 
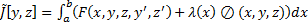с дополнительными условиями (6), т.е. 
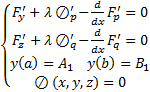Поскольку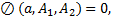 
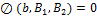, то 
будет выполнятся автоматически
Без док-ва.
ПРИМЕРЫ(?)
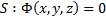
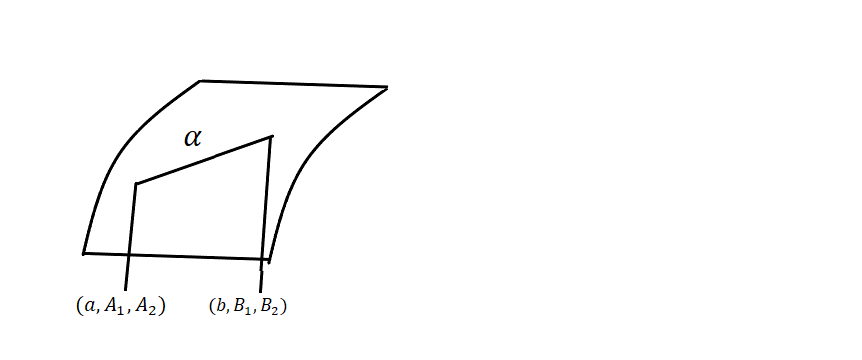
Предположим
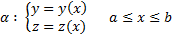
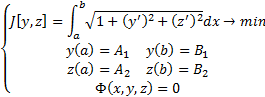
Рассмотрим задачу о геодезической линии на верхней поверхности цилиндра
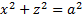
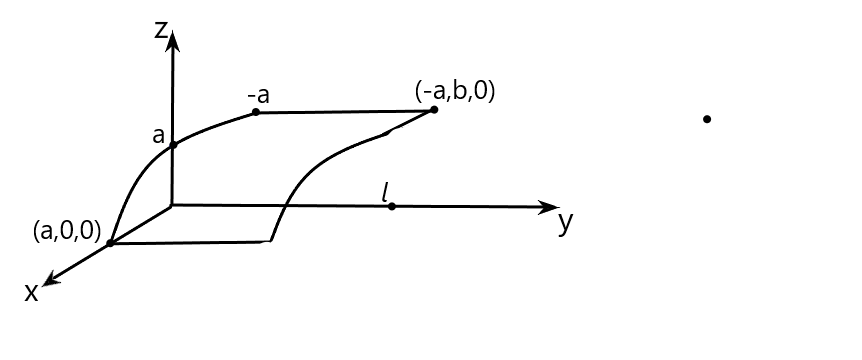
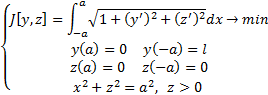
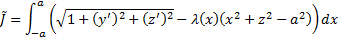
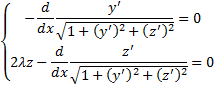
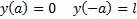
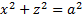
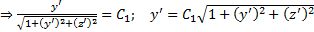
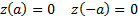
Из уравнения поверхности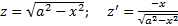 
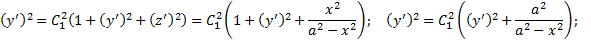
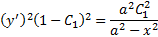
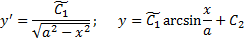
Из граничных условий :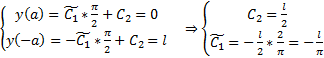 
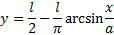
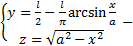геодезическая линия . Или :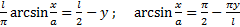 
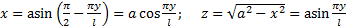т.е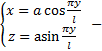 
винтовая линия