Вопрос 40 Обобщение простейшей задачи вариационного исчисления .
Пусть теперь М – множество функций из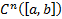 
для которого выполняются следующие условия (краевые условия)
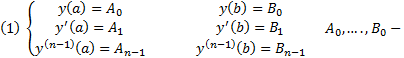фиксированные числа
Рассмотрим на М функционал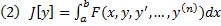 
, где 
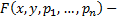заданная функция n+2 переменных
Опр. (2) называется функционалом, зависящим от высших производных
Пусть поставлена задача нахождения функционала (2) при выполнении краевых условий (1)
Теор. Если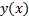 
реализует экстремум функционала (2) при краевых условиях (1), причем
1) 
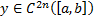
2) 
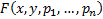непрерывна со своими производными до 
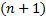порядка включительно
То 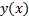является решением краевой задачи Эйлера-Пуассона.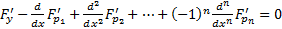 
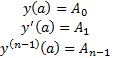
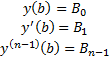
Док-во: идея доказательства аналогична предыдущему случаю, но интегрировать по частям до n раз + использовать обобщение Леммы ДОКАЗАТЬ #
Рассмотрим теперь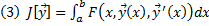 
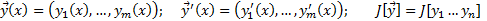
Рассмотрим функции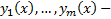 
непрерывнфе дифференцируемые и с закрепленными концами, т.е. пост краевые условия
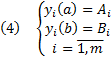или коротко 
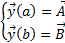. Рассмотрим задача нахождения экстремума функционала (3) при наличии краевых условий (4)
Теор. (Необходимое условие экстремума функционала с закрытыми концами, зависящими от нескольких функций)
Пусть набор функций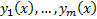 
реализует экстремум функционала (3) с закрытыми концами, причем
1) 
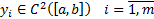
2) 
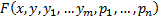непрерывна со своими производными до 2 порядка включительно
Тогда 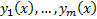удовлетворяет системе уравнений Эйлера 
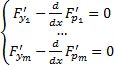крайняя задача Эйлера с дополнительными условиями (4)
Док-во: варьируется независимо друг от друга + использовать осн леммы вариационного исчисления по каждой переменной ДОКАЗАТЬ #
Вопрос 40. Важные частные случаи интегрируемости уравнения Эйлера.
Замеч. В отличие от задачи Коши, краевая задача может и не иметь решений, а может иметь неединственное решение
Примеры :
1) 
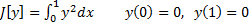. Уравнение Эйлера 
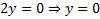. Это решение удовлетворяет краевым условиям, но если поставить поставить другие краевые условия, например
2) 
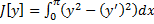
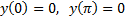
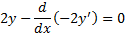
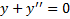
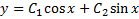
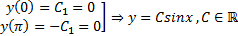имеется бесконечно много решений
Рассмотрим важные частные случаи
1) 
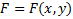(не зависит от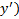 
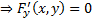(не дифференциальное уравнение, а просто конечное уравнение связи x и y). Она может неявно задавать 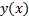, но из-за отсутствия произвола эта функция редко удовлетворяет краевым условиям, т.е. чаще всего краевая задача решения не имеет
2) 
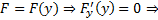если есть решение этого уравнения, то это константа 
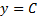, которая тоже чаще всего не удовлетворяет краевым условиям
3) 
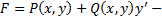линейная по 
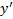функция. Тогда получим :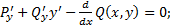 
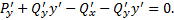Опять получаем конечное выражение 
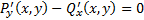эта некоторая связь между x и y, которая может явно задавать 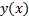, но она чаще всего не удовлетворяет краевым условиям. Если же 
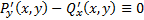, то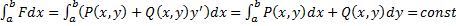 
. По любой кривой 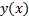значение интеграла одно и то же, т.е. вариационная задача теряет смысл.
4) 
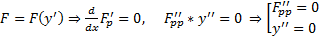Пусть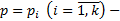 
корни уравнения 
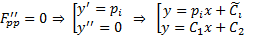в любом случае экстремали прямые линии
5) 
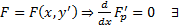первый интеграл 
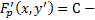это уже уравнение 1-го порядка
6) 
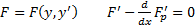. Домножим обе части на 
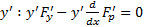добавим и вычтем в левой части 
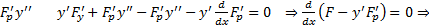имеется первый интеграл 
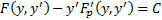Тоже порядок понизился до первого.