Вопрос 39. Простейшая задача вариационного исчисления .
Пусть М – множество дифференцируемых на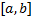 
функций 
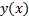, что 
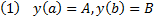A,B – произвольные числа
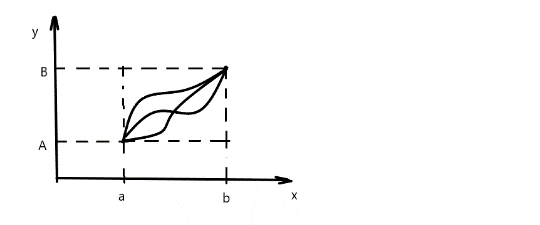
Опр. Такие кривые называются кривыми с закрепленными концами
Рассмотрим такой функционал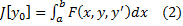 
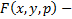определенная функция 3х переменных (условия на эту функцию уточним позже)
Опр. Задача нахождения экстремума функционала (2) на множестве непрерывных дифференцируемых функций, удовлетворяющих условию (1), называется простейшей задачей вариационного исчисления или задачей с закрытыми концами.
Было показано, что необходимое условие экстремума дифференцируемого функционала является равенство нулю его вариации. Конкретизируем необходимые условия для данного функционала
Замеч. Поскольку концы кривых закреплены, то для всех дополнительных вариаций выполняется, что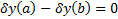 
Замеч.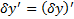 
# 
#
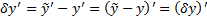Найдем вариацию (2) (по второму опр)
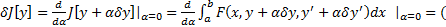дополнительно, что 
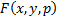обладает непрерывными производными до нужного нам порядка; тогда можно дифференцировать под знаком интеграла) 
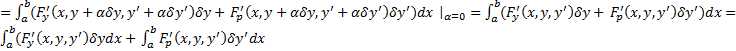. Рассмотрим второе слагаемое. 
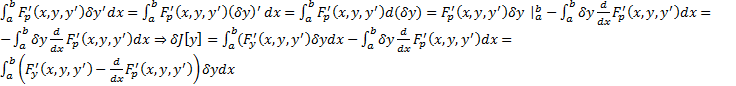. Если на 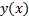достигается экстремум, то 
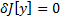, т.е. 
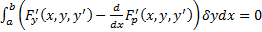. В силу произвольности 
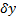, получаем, что 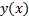должна удовлетворять уравнению.
Опр.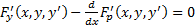 
, которое называется уравнением Эйлера.
Поскольку края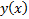 
закреплены, то на самом деле 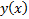должна являться решением краевой задачи, которая состоит из уравнения Эйлера и критических условий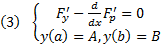 
Опр. Она называется краевой задачей Эйлера
Распишем подробно уравнение Эйлера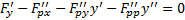 
(таким образом, это уравнение 2-го порядка относительно )
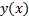Мы почти доказали следующее утверждение
Теор. (Необходимое условие экстремума функционала с закрытыми концами)
Пусть 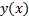реализует экстремум функционала (2) с закрытыми концами, причем :
1) 
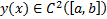
2) 
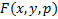непрерывна со своими производными до 2-го порядка включительно
Тогда 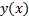является решением краевой задачи Эйлера (3). Основанием перехода от 
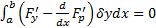к уравнению Эйлера является Лемма вариационного исчисления
Лемма. (Основная лемма вариационного исчисления)
Пусть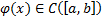 
. Если 
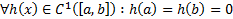выполнено, что 
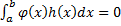, то 
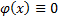на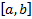 
Док-во: (от противного) Допустим, что это не так, т.е.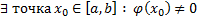 
. Поскольку 
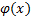непрерывна, то 
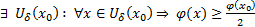. Рассмотрим 
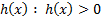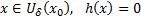при 
при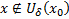 
. Тогда 
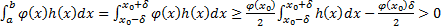. Получили противоречие(интеграл должен быть равен нулю) 
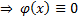на #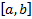
Замеч. Доказанная теорема дает необходимое условие слабого экстремума, но все, что необходимо для слабого экстремума, необходимо и для сильного .Опр. Всякое решение краевой задачи Эйлера называется экстремалью. То, таким образом, если доказано, что экстремум реализуется на дважды дифференцируемой функции, то это обязательно будет экстремаль.
Замеч. Необходимое условие достаточным не является. Поэтому, вообще говоря, не всякая экстремаль данного функционала реализует его экстремум