Вопрос 36. ТСЕ решение ЗК для уравнения 1-го порядка, разрешенного относительно производной.

Дата: 2025-05-01; Просмотры: 4
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

Доказательво существования решения

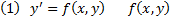определена в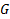

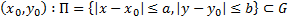
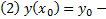начальные условия

ЗК. Найти интегральную кривую уравнения (1) проходящую через 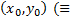найти решение (1), удовлетворяющее н.у. (2))

Теор. Пусть 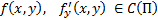. Тогда 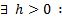в 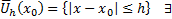решение уравнения (1) удовлетворяющее н.у. (2) и это решение единственное на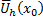

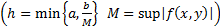
Док-во: Поэтапное доказательство существования решения

1) Докажем, что 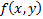удовлетворяет в П условию Липшица по переменной 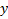, т.е. 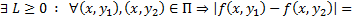теор. о конечных приращениях 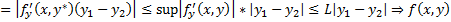удовлетворяет условию Л в П

2) Докажем, что ЗК (1), (2) эквивалентна интегральному уравнению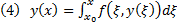

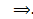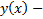## Пусть решение ЗК (1), (2). Тогда 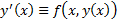. Проинтегрируем это тождество от 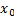до

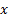
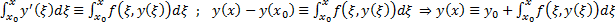
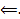Пусть 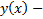решение (4). Тогда 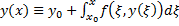Дифференцируем по 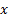, получим : 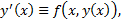причем 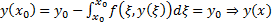является решением ЗК (1), (2)##

3) (Построение функциональной последовательности) Строим функциональную последовательность следующим образом. Везде считаем, что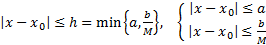

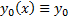
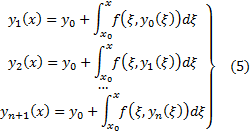
4) (Принадлежность П)

Покажем, что при 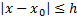выполняется, что 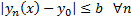т.е.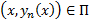

##

……

##

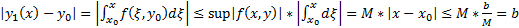
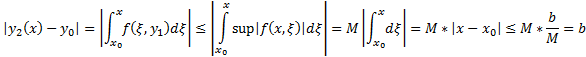
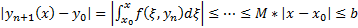5) (Абсолютная и равномерная сходимость функциональной последовательности)

Покажем, что 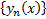сходится абсолютно и равномерно на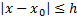

## Очевидно 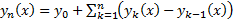Таким образом, сходимость последовательности 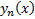эквивалента сходимости функционального ряда 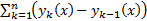(т.к.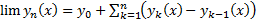
Рассмотрим 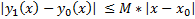. Тогда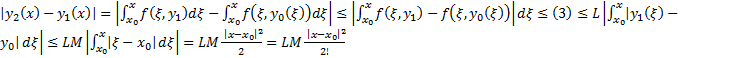

……

 

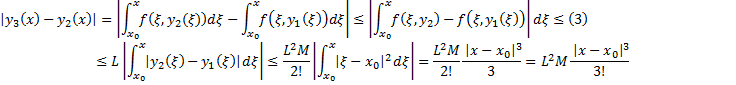
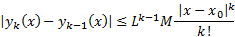
Тогда 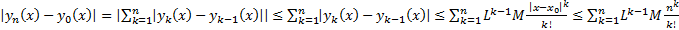Числовой ряд 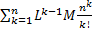Сходится по признаку Даламбера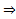 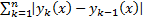мажорируется сход числовым рядом 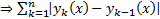сходится абсолютно и равномерно на 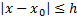по правилу Вейерштрассе. 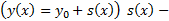сумма ряда. 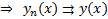причем 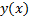непрерывна при 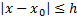в случае равномерной сходимости.

Замеч. 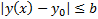в силу теоремы о предельном преходе в неравенствах

6) (Равномерная сходимость )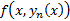

Покажем, что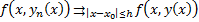

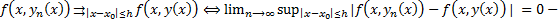## критерий сходимости функциональной последовательности. Рассмотрим ##

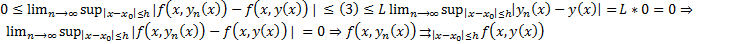7) (Решение интегрального уравнения)

Покажем, что 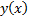является решением интегрального уравнения (4)

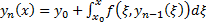## (из (5)) 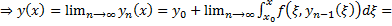в силу равномерной сходимости 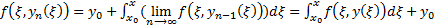Но поскольку интегрируемое уравнение (4) эквивалентно ЗК (1), (2) то 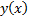и является решенной ЗК ##

Таким образом доказано, что решение ЗК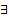

Доказательство конструктивное. Указан метод построения решения. (Метод последовательного приближения #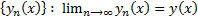

 

Вопрос 37. ТСЕ. Доказательство единственности . Элементы вариационного исчисления

Лемма. (Лемма Гронуолла)

Если 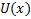непрерывна и неотрицательна на 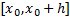и удовлетворяет условию 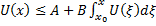, то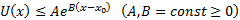

Док-во: рассмотрим 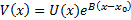, которая также непрерывна и неотрицательна на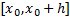 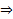достигает своей верхней грани на 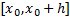. Предположим, что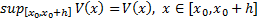

#

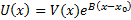
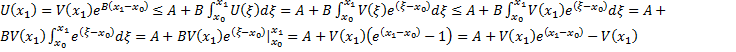
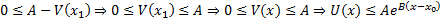Докажем теперь единственность решения ЗК на 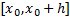(слева доказывается аналогично)

Док-во: Пусть 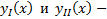решения ЗК на 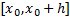. Тогда 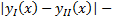непрерывно, неотрицательно на 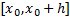и 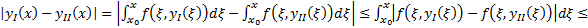условие Л в П 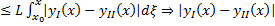удовлетворяет условию Леммы Гронуолла с #

 

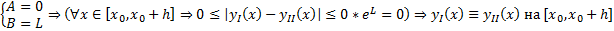Вариант 38.

ГЛАВА. ЭЛЕМЕНТЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ

Основные понятия

Пусть 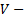ЛНП ( 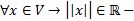норма

1) 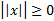,причем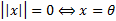

2)

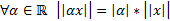
3) )

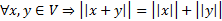Напомним, что функционалом называется правило(закон), по которому каждому элементу ЛП ставится в соответствие число.

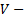вещественное ЛП

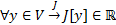
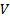считаем областью задания функционала

Замеч. Иногда функционал задан не на всем V, а на некотором его подмножестве 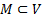. Тогда М считается областью задания функционала.

Основное ЛП, которое мы будем рассматривать, это 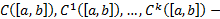ЛП функций, непрерывных на 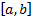со своими производными до к-го порядка включительно.

Норма в 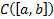вводится следующим образом :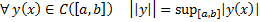

В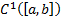

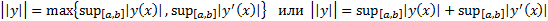
В 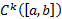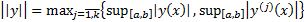или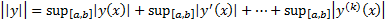

Поскольку элементами рассматриваемой ЛНП являются фактически функции 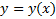, то мы их будем называть кривыми, а иногда точками, линейного пространства.

Опр. 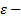окрестностью кривой 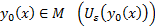называется совокупность всех кривых 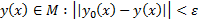. Если рассматривать , то окрестность называется сильной, а если это 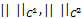и т.д. окрестность называется слабой

Опр. 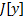называется непрерывной на кривой 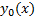, если 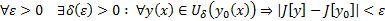(непрерывная тоже бывает слабая и сильная в зависимости от того, какая норма берется для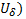

Опр. Будем говорить, что функционал 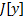достигает максимума на кривой 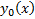, если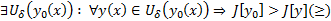 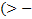строгий максимум, 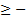нестрогий максимум) (так также может быть сильным или слабым, в зависимости от того, какая норма берется для 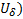. Аналогично определяется локальный минимум.

Локальный максимум или минимум будем называть локальным экстремумом функционала. Далее слово локальный будем опускать.

Замеч. Если функционал на кривой 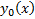достигает сильного экстремума, то он достигает и слабого, обратное неверно.

Всякое условие, необходимое для слабого экстремума, необходимо и для сильного. Это будем использовать в дальнейшем.

Опр. Если 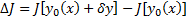можно представить в ви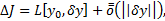де где 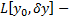линейный по 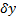функционал 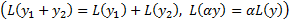, то 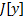называется дифференцируемым в точке 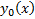, а 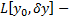его вариацией в точке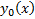

Опр. Пусть 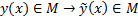Тогда 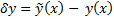называется вариацией кривой(т.е. вариация кривой это произвольное ее приращение)

Опр. Пусть 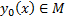. Рассмотрим 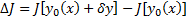. Эту разность назовем приращением функционала

Опр. Пусть число 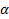достаточно мало, так что 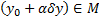. Тогда если 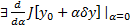, то она называется вариацией функционала 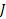в точке 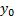(в узком смысле)

Можно показать, что если функционал является дифференцируемым в узком смысле, то он будет дифференцируем и в широком смысле, причем обе вариации при этом совпадают. Обратное, вообще говоря, неверно. Однако для интегральных, которые мы будем рассматривать, это одно и то же. Но вариация в узком смысле проще вычисляется, поэтому будем дальше пользоваться вторым(т.е. в узком смысле)

Теор. (Необходимое условие экстремума дифференцируемого функционала)

Если дифференцируемый функционал 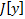достигает экстремума во внутренней точке 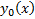множества М ( 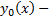внутренняя точка М, если 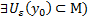, то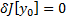

Док-во: Пусть ради определенности на кривой 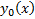достигается минимум 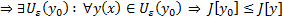. Возьмем произвольную ненулевую вариацию 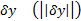. Рассмотрим всевозможные 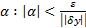. Тогда 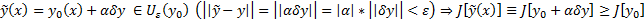. Рассмотри функцию одного переменного : 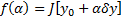. Тогда для тех же 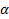выполняется, что 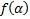достигает минимума в точке 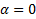, т.к. 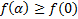. Поскольку 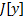дифференцируем в точке 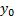, то 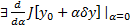, но эта производная будет равна 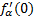. А в точке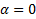 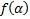достигает минимума 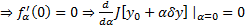, т.е. #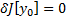