Вопрос 34. Неоднородные ЛОДУ ВП с постоянными коэффициентами .
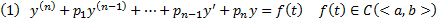
Напомним, что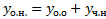 
В случае произвольной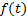 
ищем 
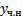методом вариации произвольных постоянных. Однако в случае специального вида 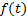удобнее применять метод неопределенных коэффициентов
Теор. (принцип суперпозиции)
Если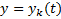 
является решением уравнения 
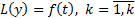, то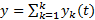 
является решением уравнения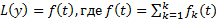 
Док-во: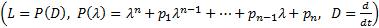 
#
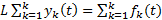Пусть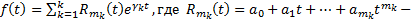 
многочлен степени 
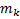с определенными коэффициентами, 
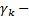произвольная(комплексная)
В силу принципа суперпозиции рассмотрим поиск 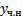для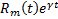 
Возможны 2 случая :
1) 
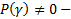нерезонансный случай
2) 
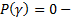резонансный случай
Нерезонансный случай
Пусть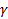 
не является корнем характеристического уравнения :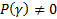 
Теор. Если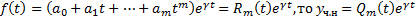 
. Где 
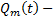многочлен той же степени, что и 
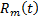, коэффициенты которого определяются единственным образом
Док-во: Подставим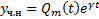 
в уравнение 
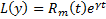используя диф тождество : 
. Тогда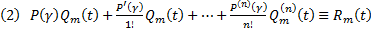 
Рассмотрим ЛО, действующую ЛП многочленов степени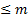 
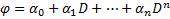Тогда (2) примет вид 
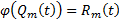. Покажем, что 
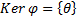т.е. ядро состоит только из многочлена 
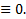От противного. Предположим, что 
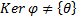. Тогда 
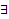многочлен 
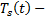многочлен степени s : 
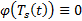. Но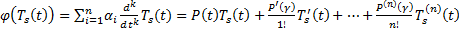 
. Тогда если s=0, т.е. 
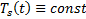, то первое слагаемое 
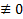, а остальные 
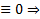невозмодно, чтобы 
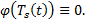Если же 
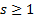, то первое слагаемое будет многочленом степени s , а остальные слагаемы е имеют степень <s 
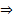невозможно, чтобы сумма 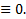Мы пришли к противоречию : 
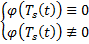Таким образом получаем, что 
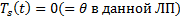. Таким образом 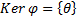. Тогда 
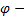обратим, т.е. 
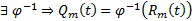, т.е. по заданному многочлену 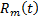многочлен 
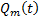определяется единственным образом
Замеч. На практике полагают, что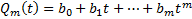 
, подставляем 
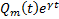в уравнение 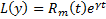, получают точку, сокращают обе части на 
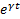и приравнивают коэффициенты при степени t , получа.т СЛАУ из 
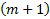уравнений с 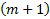неизвестными
Вопрос 35.
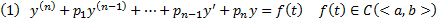
Напомним, что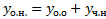
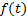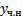В случае произвольной ищем методом вариации произвольных постоянных. Однако в случае специального вида 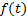удобнее применять метод неопределенных коэффициентов
Теор. (принцип суперпозиции)
Если 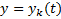является решением уравнения 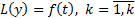, то 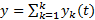является решением уравнения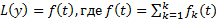
Док-во: #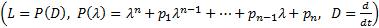
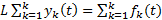Пусть 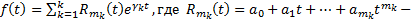многочлен степени 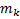с определенными коэффициентами, 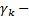произвольная(комплексная)
В силу принципа суперпозиции рассмотрим поиск 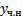для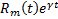
Возможны 2 случая :
1) 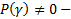нерезонансный случай
2) 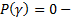резонансный случай
Резонансный случай .
Пусть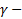 
корень характеристического уравнения кратности k :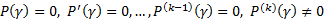 
Теор. Если 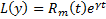, то 
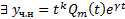, где 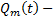многочлен той же степени, что и 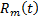и его коэффициенты по данным коэффициентам 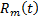определяются единственным образом.
Док-во: Используя диф тождество, подставим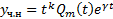 
в уравнение 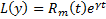, получим : 
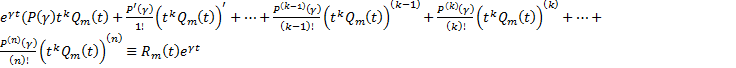. Рассмотрим ЛО 
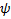, действующего в ЛП многочлена степени 
. 
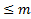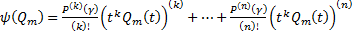. Тогда 
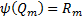. Покажем, что 
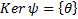. От противного. Пусть 
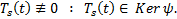Тогда 
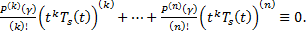Если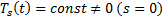 
, получим 
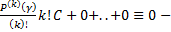невозможно. Если же 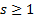, первое слагаемое многочлена степени s , а остальные слагаемые имеют степень < s, т.к. там берутся более высшие производные 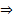невозможно чтобы сумма = 0. Пришли к противоречию 
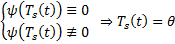, т.е. нулевой многочлен. Таким образом 
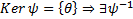Он определяется единственным образом. 
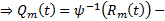определяется единственным образом
Замеч. На практике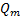 
отыскивают подставляя 
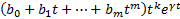в уравнение 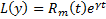, сокращая 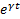и приравнивая коэффициенты при одинаковых степенях t. Получают СЛАУ из 
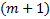неизвестных. Из док-ва теоремы получаем, что она имеет единственное решение.
Если уравнение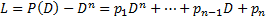 
имеет действительные коэффициенты 
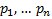, а 
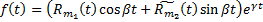, где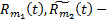 
многочлены степеней 
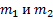с действительными коэффициентами, 
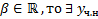в ви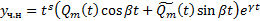де 
, где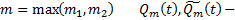 
многочлены степени m с действительными коэффициентами 
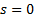, если 
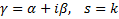, если 
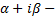корень кратности k