Вопрос 22. Замечания о построении ФСР в случае кратных корней
Рассмотрим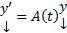 
Будем искать ее решение в виде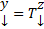 
. Где Т – построенная невырожденная матрица. Тогда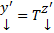 
. 
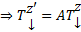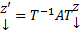Допустим, что матрица А диагонализуема (т.е. линейный оператор, которому она отвечает в некотором базисе имеет диагонализуемую матрицу. Это возможно 
базис из СВ этого ЛО 
у всех его СЗ АК=ГК. В этом случае Т представляет собой матрицу, в столбцах которой записаны координаты собственных векторов ) Предположим, что 
базис из СВ. Тогда 
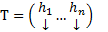
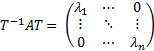Тогда получим, что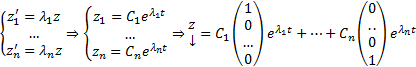 
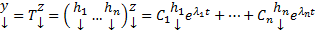Таким образом независимо от того являются ли корни характеристического уравнения простыми или нет, в случае, когда 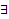базис из СВ, отвечающий этим СЗ, ФСР имеет один и тот же вид, а именно 
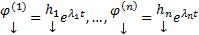с той лишь разницей, что в случае кратных корней некоторые 
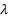могут совпадать.
В случае когда хотя бы для одного 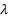АК > ГК (ради определенности пусть АК =k, ГК=m m<k) можно показать, что 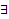k ЛНЗ решений, отвечающих такому 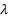, который имеет вид 
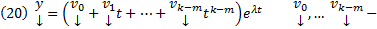столбцы подлежащие определению : Как их отыскать ? Подставим (20) в 
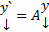получим тождество 
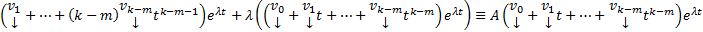Далее приравниваем коэффициенты при одинаковых степенях t получим :
…………..
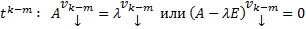
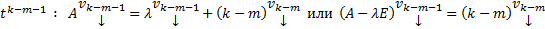
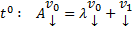
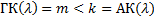
Теор. 
ЛНЗ решений вида 
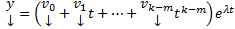, отвечающих этому СЗ(без док-ва)
Подставим в ОСЛОДУ, получим, что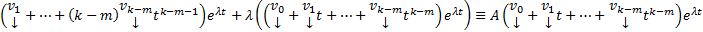
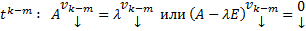, т.о.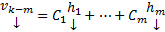 
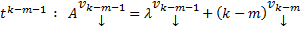Эта система обладает расширенной матрицей 
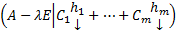и совместна при всех значениях 
. Из условия совместимости получаем ограничения на , т.е. связь между ними, т.е. будет зависеть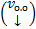 
от m новых констант 
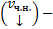будет зависеть от некоторых старых (это же касается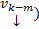 
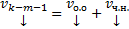
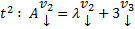
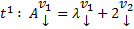
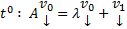
Постепенно, спускаясь вниз, будем на каждом шаге получать m новых констант и дополнительных ограничений на старые константы. В конце останется k констант. Собирая коэффициенты при них мы получим k элементов ФСР отвечающих данному .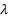
Вопрос 23. Неоднородные СЛОДУ с постоянными коэффициентами .
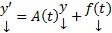
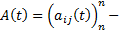постоянная матрица.
В общем случае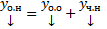 
. Если 
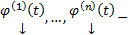ФСР ОСЛОДУ (1) 
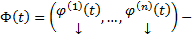ФМР. Тогд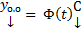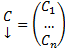а 
, 
, а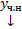 
отыскиваем, полагая 
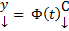(метод вариации произвольных постоянных). Однако в случае, когда 
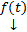имеет специальный вид, удобнее использовать метод неопределенных коэффициентов.
Теор. (принцип суперпозиции)
Если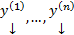 
является решениями соответствующей системы 
,
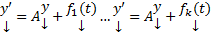то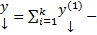 
является решением системы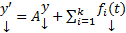 
ДОКАЗАТЬ
Метод неопределенных коэффициентов.
Теор. Если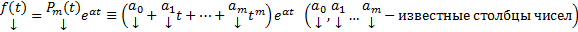 
,
то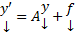 
имеет r решений вида :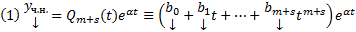 
. 
не является корнем характеристического уравнения 
. 
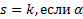являются корнем характеристического уравнения 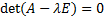алгебраической кратности k. Неизвестные столбцы могут быть найдены путем подстановки решений вида (1) в неоднородную СЛОДУ и приравнены коэффициенты при степенях t в правой и левой частях. (без доказательства)
Теор. Если А – вещественная матрица, а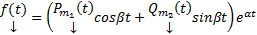 
, где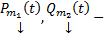 
векторные многочлены с действительными коэффициентами, 
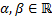, тогда система 
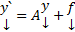обладает частным решением такого вида : 
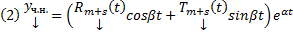, где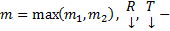 
векторные многочлены с действительными коэффициентами 
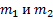соответственно. . 
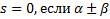не является корнем характеристического уравнения . 
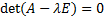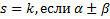являются корнем характеристического уравнения 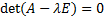алгебраической кратности k. Коэффициенты многочленов R и T определяются путем подстановки решений вида (2) в неоднородную СЛОДУ 
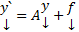и приравнивая коэффициенты при 
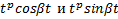в обеих частях 
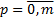(без док-ва)