Линейные нормальные системы.
Рассмотрим (1)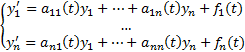 
Будем считать, что 
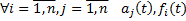определены и непрерывны на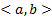 
Опр. (1) называется линейной нормальной(СЛОДУ) системой (ОДУ 1-го порядка) (сама система имеет порядок n)
Введя обозначение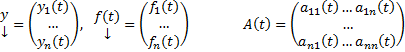 
перепишем (1) в виде 
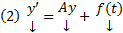. Если 
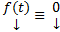(т.е. 
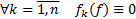на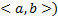 
, то СЛОДУ (1) (или (2)) называется однородной, в противном случае – неоднородной
Опр. ЗК для СЛОДУ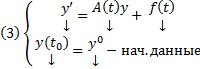 
Теор.(ТСЕ для СЛОДУ)
Если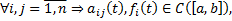 
то на всем 
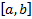при любом наборе начальных данных 
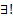решение ЗК (3) на всем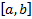
Без доказательства
Вопрос 13 Линейно зависимые и независимые строки матрицы
(1) 
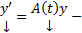ОСЛОДУ (3)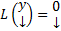 
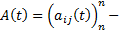матрица непрерывна на 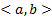функций (коэффициенты системы). Напомним, что в ЛП столбцов функций (высоты h) столбцы 
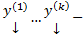называется ЛЗ, если 
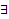нетривиальный набор чисел 
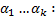(2) 
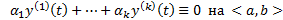. Если тождество (2) выполняется только при 
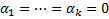, то система 
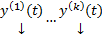ЛНЗ
Опр. Система столбцов называется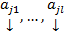 
линейно зависимой, если 
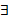нетривиальный набор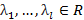 
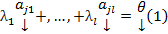. Если же (1) возможно только при 
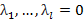, то система столбцов линейно независима.
Опр. Система строк называется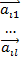 
линейно зависимой, если 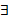нетривиальный набор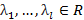 
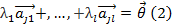. Если же (2) возможно только при 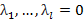, то система строк линейно независима.
Достаточные условия о ЛЗ и ЛНЗ:
1. Система столбцов, содержащая нулевой столбец, линейно зависимая
# ЛЗ и ЛНЗ сохраняются при любой нумерации столбцов, поэтому БОО можно считать что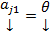 
,
тогда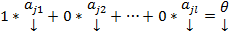 
=>это НТЛК =>ЛЗ #
2. Система столбцов, содержащая ЛЗ подсистему, ЛЗ
# БОО считаем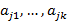 
линейно зависимая подсистема,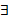 
: 
=> 
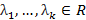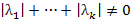
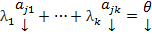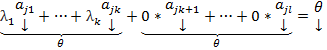это НТЛК => это ЛЗ#
3. Любая подсистема ЛНЗ системы столбцов является ЛНЗ
# Из предположения, что подсистема ЛЗ => система является ЛЗ, но по условию система столбцов является ЛНЗ => противоречие, значит подсистема ЛНЗ #
(Аналогично для системы строк)
Критерий ЛЗ:
Система столбцов является ЛЗ ó один из них является линейной комбинацией остальных.
ð 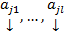- ЛЗ система столбцов, 
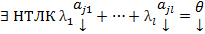, БОО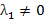 
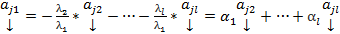, т.е. 
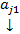- ЛК остальных
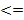Пусть один из столбцов ЛК остальных БОО считаем 
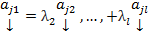Тогда
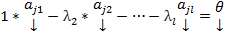- это НТЛК=> 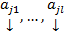линейно зависимая система
Вопрос 14. Однородные СЛОДУ . Свойства решений
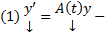ОСЛОДУ
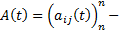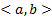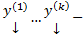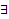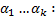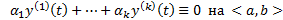матрица непрерывна на функций (коэффициенты системы). Напомним, что в ЛП столбцов функций (высоты h) столбцы называется ЛЗ, если нетривиальный набор чисел (2) . Если тождество (2) выполняется только при 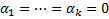, то система 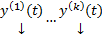ЛНЗ
Свойства решений ОСЛОДУ
1) (Тривиальность) ОСЛОДУ (1) всегда обладает решением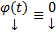 
Док-во: очевидно
2) (Линейность) Если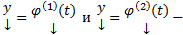 
некоторые решения (1), то 
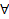чисел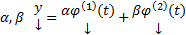 
также является решением (1)
Док-во: Введем в ЛП столбцов функций оператор L: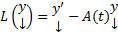 
, тогда систему (1) можно переписать в виде (3) 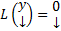. Пусть 
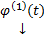и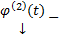 
решения, т.е. 
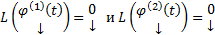. Тогда 
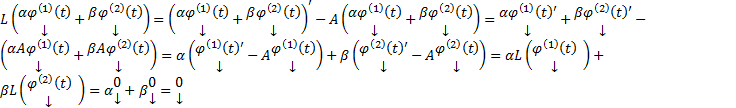. Сейчас доказано, что L является линейным оператором и что любая ЛК решения также является решением.
Замеч. Из 1) и 2) следует, что совокупность всевозможных решений ОСЛОДУ (1) образует ЛП, которое обозначим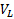 
3) (О нуле решения) Если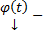 
решение (1) или (3) с непрерывными коэффициентами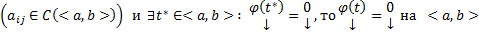 
Док-во: Рассмотрим ЗК для (1) :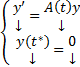 
С одной стороны 
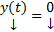является ее решением, с другой стороны 
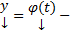тоже ее решение. Но по ТСЕ на всем 
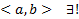Решение ЗК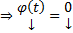 
4) (О линейной зависимости)
Пусть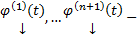 
решение (1) (или (3)) . Тогда эта система решения является ЛЗ
Док-во: Рассмотрим эту систему при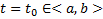 
. При фиксированном 
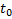это просто набор из 
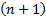столбца высоты 
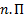оскольку ЛП столбцов чисел высоты 
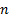имеет размерность 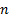, то система 
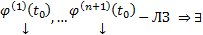нетривиальный набор 
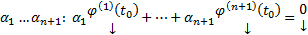(4). Рассмотрим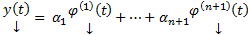 
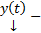ЛК решений (1) 
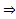является решением (2), причем 
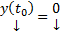в соответствии с (4). Таким образом 
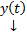является решением ЗК 
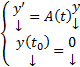, но эта ЗК также обладает решением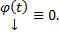 
По ТСЕ получаем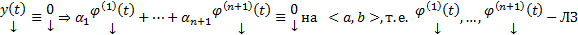 
5) (О линейной независимости)
ОСЛОДУ (1) (или (3)) с непрерывными коэффициентами обладает n ЛНЗ решениями
Док-во: Рассмотрим набор столбцов :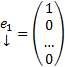 
, 
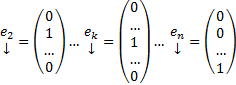и рассмотрим n штук ЗК : 
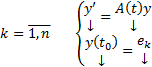где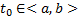 
. Пусть 
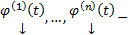решения этих ЗК соответственно. Предположим, что эта система решений ЛЗ. Тогда 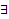нетривиальный набор 
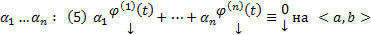. Тогда (5) должно быть выполнено и при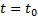 
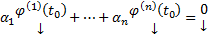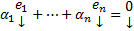т.е.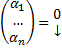 
т.е. 
т.е.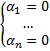 
. Противоречие тому, что набор 
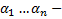нетривиально. Оно вызвано из предположения что 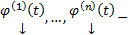ЛЗ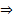 
эта система ЛНЗ на .
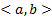Сл . Из 4 и 5 получаем, что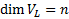 
(отсюда любой базис 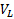содержит ровно 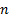элементов)
Вопрос 15.
(1) 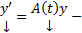ОСЛОДУ
(3)
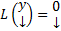
Опр. Любой базис в 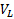назовем фундаментальной системой решений (ФСР) : ОСЛОДУ (1) (или(3)). Т.е. ФСР это упорядоченный набор из n ЛНЗ решений ОСЛОДУ (и всякое решение может быть передано как ЛК элементов этого набора)
6) (Об общем решении ОСЛОДУ)
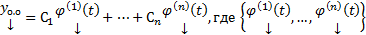назовем ФСР ОСЛОДУ, 
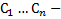произвольные постоянные
Док-во: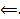 
Поскольку 
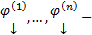базис, то любое решение является ЛК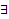 
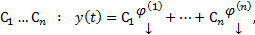
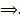Из свойства линейности любая ЛК 
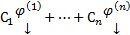является решением.