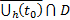Вопрос 11 Уравнение n -го порядка. Уравнения, допускающие понижения порядка
А) Простейшее уравнение n -го порядка
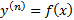, где 
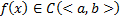. Проинтегрировав это уравнение по x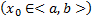 
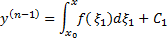
Далее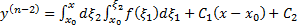 
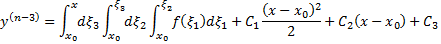
Через некоторое количество шагов
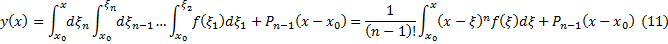
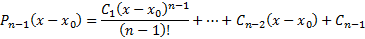
Док-во: Докажем (11) методом математической индукции.
БАЗА.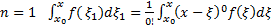 
(верно)
ШАГ. Пусть утверждение верно для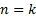 
, т.е. 
.
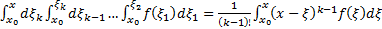Тогда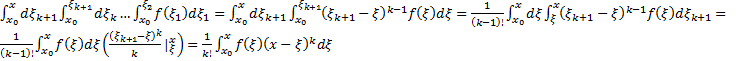 
, т.е. формула верна и для 
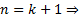утверждение верно.
Таким образом, простейшее уравнение n-го порядка всегда интегрируемо в квадратурах имеет вид (11) #
Теперь докажем, что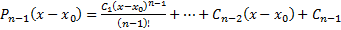 
Док-во: Применим метод ММИ. БАЗА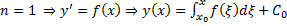 
, т.е. 
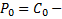верно . ШАГ Пусть утверждение верно для 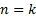, то есть выполнено 
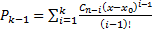. Тогда 
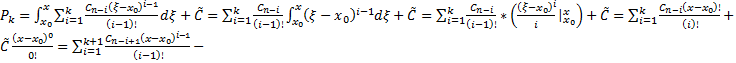верно, то есть формула верна и для 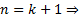утверждение верно 
#
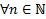Таким образом, простейшее уравнение n-го порядка всегда интегрируется в квадратурах, и его решение имеет вид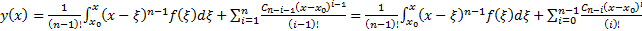 
Б) Уравнения, допускающие понижения порядка
а)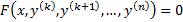 
, то подстановкой 
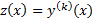уравнение понижается на к единиц 
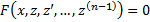. Допустим, что решение 
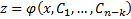. Тогда полученный промежуточный интеграл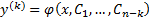 
б)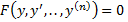 
x не входит в уравнение в явном виде. Порядок уравнения можно понизить на единицу заменой переменных 
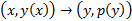, где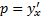 
. Если 
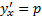, то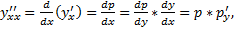 
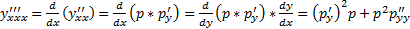. Вообще 
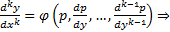уравнение принимает вид 
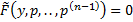решаем уравнение и получаем 
.
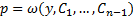Далее решаем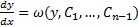 
В)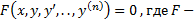 
однородное, то аргумент 
,
т.е.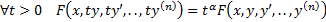 
.
В этом порядок уравнения можно понизить на 1 заменой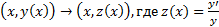 
.
В этом случае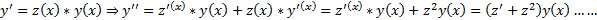 
Докажем методом ММИ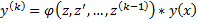 
БАЗА для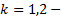 
верно(см.выше)
ШАГ индукции. Допустим, что утверждение верно для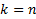 
, докажем что оно также верно для 
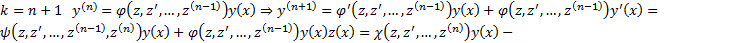верно , то есть утверждение справедливо 
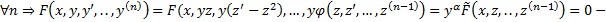уравнение (n-1) порядка
Г) Допустим, что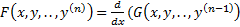 
, тогда уравнение 
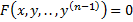имеет первый интеграл 
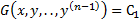. Порядок снижается на 1.
Вопрос 12. Нормальные системы ОДУ 1-го порядка.
Рассмотрим (1)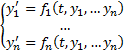 
Где t – независимая переменная, 
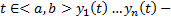неизвестные функции; 
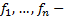заданные функции на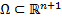 
Система ОДУ (1) называется нормальной системой ОДУ 1-го порядка(НСОДУ) с n неизвестными функциями. Само число n называется порядком системы.
Любое уравнение 1-го порядка, разрешенное относительно ст.производной :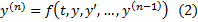 
можно свести к нормальной системе следующим образом:
Пусть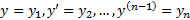 
, тогда получим нормальную систему, равносильную уравнению (2) : 
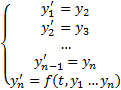(3)
Опр. Частным решением НСОДУ (1) называется совокупность дифференцируемых на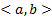 
функций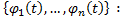 
1) 
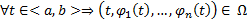
2) 
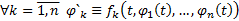на всем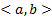
Опр. Совокупность всех частных решений НСОДУ (1) образуют общее решение
Ниже будет показано, что общее решение системы n-го порядка зависит от n произвольных постоянных.
Далее введем обозначение :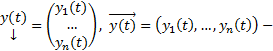 
столбец и строка неизвестных функций. 
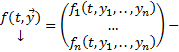столбец правых частей
В этих обозначениях (1) можно переписать в эквивалентном виде :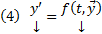 
. Тогда частное решение (4) это вектор столбец 
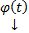(или вектор строка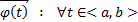 
1) 
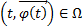
2) 
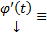
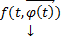
Пусть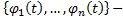 
какое-либо решение НСОДУ(1). По мере того, как t пробегает значения на 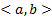, точка 
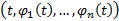пробегает некоторую траекторию в 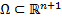она называется интегральной кривой НСОДУ (1)
n-мерное пространство переменных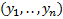 
назовем фазовым пространством , а проекцию интегральной кривой на фазовое пространство называется фазовой траекторией.
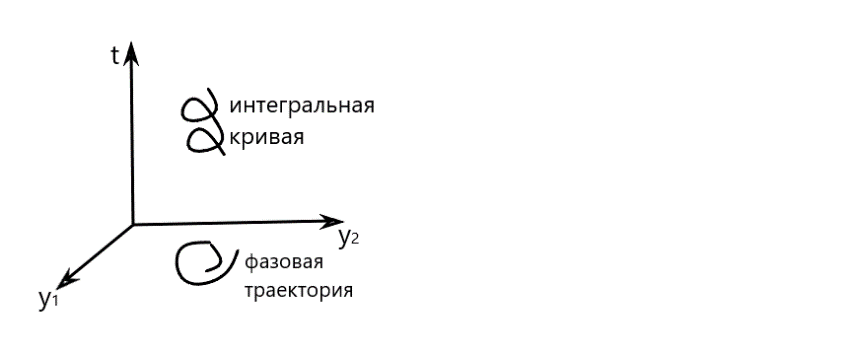
Поскольку НСОДУ (1) или (4) имеет бесконечно много решений (соответственно бесконечно много интегральных кривых), имеет смысл задача выделения интегральной кривой, удовлетворяющей некоторым дополнительным(начальным) условиям.
Опр. Задача нахождения НСОДУ(1)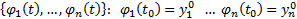 
(где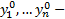 
набор начальных данных) называется ЗК для НСОДУ (1)
Коротко ЗК формулируется так :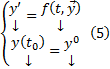 
Подразумевается, что 
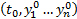является внутренней точкой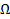 
Теор.(ТСЕ)
Пусть 
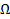внутренняя точка и в некоторой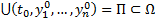 
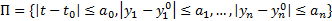выполняется, что
1) 
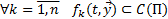
2) 
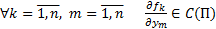Тогда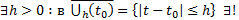 
решение ЗК (5)
Замеч. Если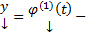 
решение ЗК (5) н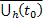а 
, а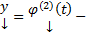 
решение ЗК (5) на некотором D, то 
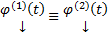на 