Вопрос 9 Уравнение Лагранжа и уравнение Клеро
Опр. Уравнение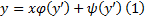 
, где 
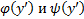непрерывные и дифференцируемые функции своего аргумента на некотором интервале , причем 
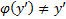, наз. уравнением Лагранжа. Применим к его решению метод введения параметра :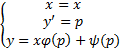 
Поскольку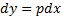 
С другой стороны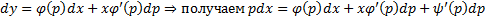 
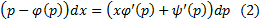Тогда уравнение (2) имеет решение 
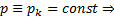уравнение Лагранжа (1) обладает решением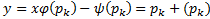 
Далее приведем (2) к виду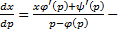 
это линейное неоднородное уравнение относительно 
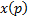. Оно всегда интегрируемо в квадратурах. Пусть его общее решение 
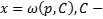произвольная постоянная. Тогда в параметрической форме решение уравнения Лагранжа задается следующим образом 
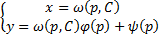Итого всевозможные решения уравнения Лагранжа (общее решение) будет :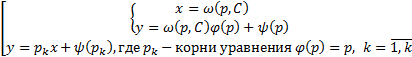 
Пусть теперь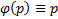 
, т.е. рассмотрим уравнение (3)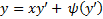 
Опр. Уравнение (3) называется уравнением Клеро
Решим его методом введения параметра. Имеем :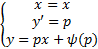 
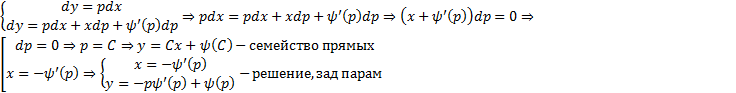
Таким образом, всевозможные решения уравнения Клеро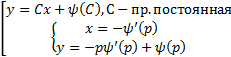 
Как соотносятся эти решения? Можно показать, что кривая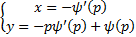 
являются огибающей семейство прямых 
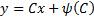, если 
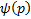не является линейной функцией.
Вопрос 10. Уравнения высших порядков, интегрируемые в квадратурах или допускающие понижения порядка.
Пусть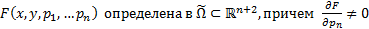 
Опр.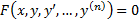 
(1) называется ОДУ n-го порядка, не разрешенного относительно старшей производной.
Допустим в некоторой области оно приводится к виду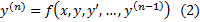 
, где f определена в 
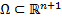, то
Опр. (2) называется ОДУ 1-го порядка, разрешенном относительно старшей производной
Опр. Частным решением уравнения (1) или (2) называется функция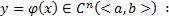 
1) 
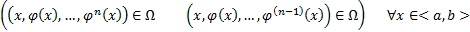
2) 
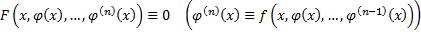на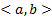 
Совокупность всевозможных частных решений образует общее решение.
ЗК для (2) ставится следующим образом:
Нужно отыскать решения уравнения (2), удовлетворяющие дополнительному условию (называется начальными условиями)
…
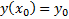
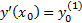
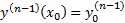
Т.е.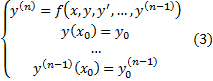 
Теор. (ТСЕ решения ЗК (3) )
Если в некоторой области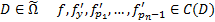 
,а точка 
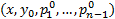является внутренней точкой области D , то 
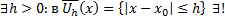решение ЗК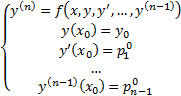 
В области существования и единственности решения общее решение уравнения (2) зависит от n произвольных постоянных т.е.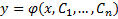 
называется общим решением уравнения (2) если всякое частное решение (2) получено при некотором значении 
, а при любом наборе значений 
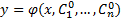представляет собой решение (2). Если это решение задано в неявном виде 
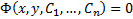, то говорят об общем интеграле уравнения (2).
Соотношение вида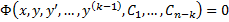 
являющееся следствием уравнения (2), называется частным интегралом этого уравнения. Например, соотношение 
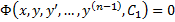или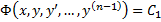 
, является следствием уравнения (2), называется первым интегралом. Т.е. функция 
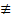const, но сохраняет постоянное значение на любом решении уравнения (2)