ЗАДАНИЕ N 24 отправить сообщение разработчикам Тема: Числовые характеристики случайных величин Дискретная случайная величина X задана законом распределения вероятностей: Тогда ее дисперсия равна …
| 7,56 | ||
| 3,2 | |||
| 3,36 | |||
| 6,0 |
ЗАДАНИЕ N 25 отправить сообщение разработчикам
Тема: Полная вероятность. Формулы Байеса
С первого станка на сборку поступает 20% , со второго – 30%, с третьего – 50% всех деталей. Среди деталей первого станка 1% бракованных, второго – 2%, третьего – 3%. Тогда вероятность того, что поступившая на сборку деталь бракованная, равна …
|
| 0,023 | ||
| 0,024 | |||
| 0,02 | |||
| 0,017 |
ЗАДАНИЕ N 26 отправить сообщение разработчикам
Тема: Однородные дифференциальные уравнения
Дифференциальное уравнение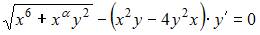 
будет однородным дифференциальным уравнением первого порядка
при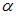 
, равном …
|
| 4 | ||
| 2 | |||
| 0 | |||
| 6 |
Решение:
Запишем уравнение в виде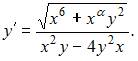 
Это уравнение будет однородным, если функция 
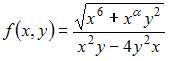будет однородной относительно 
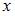и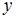 
нулевого порядка, то есть при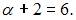 
Откуда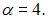 
ЗАДАНИЕ N 27 отправить сообщение разработчикам
Тема: Типы дифференциальных уравнений
Уравнение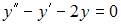 
является …
|
| линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами | ||
| линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами | |||
| уравнение Бернулли | |||
| уравнением Эйлера |
Решение:
Уравнение 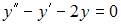можно представить в виде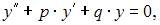 
где p и q – числа. Поэтому данное уравнение является линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами.
ЗАДАНИЕ N 28 отправить сообщение разработчикам
Тема: Системы двух линейных дифференциальных уравнений с постоянными коэффициентами
Функции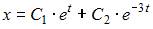 
и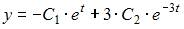 
являются решением системы дифференциальных уравнений …
|
| 
| ||
| |||
| |||
|
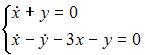
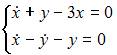
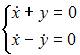
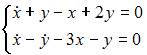
Решение:
Найдем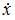 
и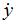 
: 
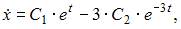
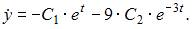Подставив 
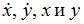в систему 
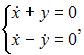видим, что второе уравнение не обращается в тождество. Подставляя 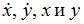в системы 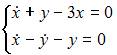и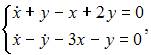 
получаем, что оба уравнения не обращаются в тождество. При подстановке 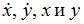в систему 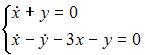оба уравнения обращаются в тождество. Следовательно, функции 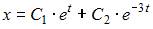и 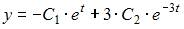являются решением системы дифференциальных уравнений .
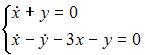ЗАДАНИЕ N 29 отправить сообщение разработчикам
Тема: Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
Общий вид частного решения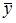 
линейного неоднородного дифференциального уравнения второго порядка 
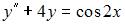будет выглядеть как …
|
| 
| ||
| |||
| |||
|
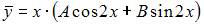
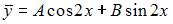
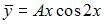
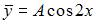
ЗАДАНИЕ N 30 отправить сообщение разработчикам
Тема: Численные методы решения дифференциальных уравнений и систем
Решение дифференциального уравнения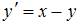 
на отрезке 
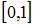с шагом 
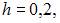при начальном условии 
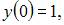в точке x = 0,2 по методу Эйлера может быть найдено как …
|
| 
| ||
| |||
| |||
|
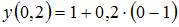
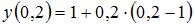
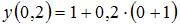
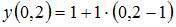
ЗАДАНИЕ N 31 отправить сообщение разработчикам
Тема: Численное дифференцирование и интегрирование
На рисунке
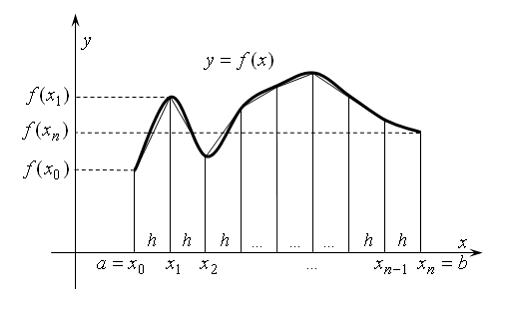
изображена геометрическая интерпретация приближенного вычисления определенного интеграла методом …
|
| трапеций | ||
| правых прямоугольников | |||
| парабол | |||
| левых прямоугольников |
Решение:
Как известно, геометрический смысл определенного интеграла от неотрицательной непрерывной на отрезке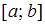 
функции f (x) состоит в том, что 
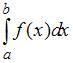равен площади криволинейной трапеции, ограниченной осью Ox, прямыми 
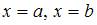и графиком функции y= f (x). Для получения приближенного значения этой площади (этого интеграла) разобьем отрезок 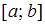на n равных частей с длинами h точками 
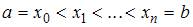и заменим каждую «маленькую» криволинейную трапецию с высотой h на обычную трапецию с высотой h и основаниями, равными значениям функции в левом и правом конце каждого частичного отрезка – 
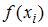и 
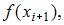где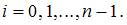 
Сумма площадей полученных обычных трапеций приближенно равна сумме площадей маленьких криволинейных трапеций. Данный метод замены 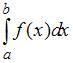на сумму 
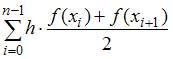называется методом трапеций приближенного нахождения определенного интеграла.
ЗАДАНИЕ N 32 отправить сообщение разработчикам
Тема: Интерполирование функций: интерполяционные полиномы Лагранжа
Функция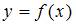 
задана таблично:
В интерполяционном полиноме Лагранжа 2-ой степени с узлами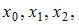 
составленном по этой таблице для приближенного вычисления 
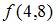при условии 
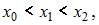значение 
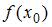не может быть равно …
|
| 12 | ||
| 6 | |||
| 5 | |||
| 8 |