ЗАДАНИЕ N 1 отправить сообщение разработчикам Тема: Градиент скалярного поля Модуль градиента скалярного поля в точке пересечения оси Oz с поверхностью равен …

| 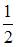
| ||
| 1 | |||
| 2 | |||
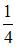
|
 ЗАДАНИЕ N 2 отправить сообщение разработчикам
ЗАДАНИЕ N 2 отправить сообщение разработчикам
Тема: Векторное произведение векторов
Векторное произведение векторов 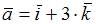 и
и 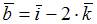 равно …
равно …

| 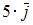
| ||
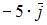
| |||
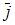
| |||
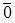
|
Решение:
Вычислим
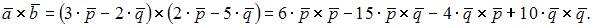
Так как 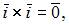
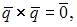
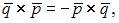 то
то 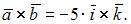 Векторное произведение ортов
Векторное произведение ортов 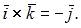 Следовательно
Следовательно 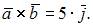
 ЗАДАНИЕ N 3 отправить сообщение разработчикам
ЗАДАНИЕ N 3 отправить сообщение разработчикам
Тема: Норма вектора в евклидовом пространстве
В евклидовом пространстве со стандартным скалярным произведением норма вектора 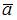 равна 2, норма вектора
равна 2, норма вектора 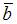 равна 3, их скалярное произведение равно 2. Тогда норма вектора
равна 3, их скалярное произведение равно 2. Тогда норма вектора 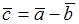 равна …
равна …

| 3 | ||
| 1 | |||
| 9 | |||
| –1 |
 ЗАДАНИЕ N 4 отправить сообщение разработчикам
ЗАДАНИЕ N 4 отправить сообщение разработчикам
Тема: Интервальные оценки параметров распределения
Построен доверительный интервал для оценки математического ожидания нормально распределенного количественного признака при известном среднем квадратическом отклонении генеральной совокупности. Тогда при уменьшении объема выборки в два раза значение точности этой оценки …

| увеличится в 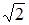 раз раз
| ||
| уменьшится в два раза | |||
| увеличится в два раза | |||
уменьшится в 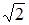 раз раз
|
 ЗАДАНИЕ N 5 отправить сообщение разработчикам
ЗАДАНИЕ N 5 отправить сообщение разработчикам
Тема: Статистическое распределение выборки
Из генеральной совокупности извлечена выборка объема 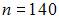 :
:
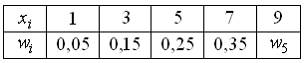
Тогда частота варианты 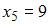 в выборке равна …
в выборке равна …

| 28 | ||
| 63 | |||
| 42 | |||
| 35 |
 ЗАДАНИЕ N 6 отправить сообщение разработчикам
ЗАДАНИЕ N 6 отправить сообщение разработчикам
Тема: Элементы корреляционного анализа
При построении выборочного уравнения парной регрессии вычислены выборочный коэффициент корреляции 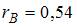 и выборочные средние квадратические отклонения
и выборочные средние квадратические отклонения 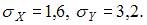 Тогда выборочный коэффициент регрессии Y на X равен …
Тогда выборочный коэффициент регрессии Y на X равен …

| 1,08 | ||
| –1,08 | |||
| 0,27 | |||
| –0,27 |
 ЗАДАНИЕ N 7 отправить сообщение разработчикам
ЗАДАНИЕ N 7 отправить сообщение разработчикам
Тема: Точечные оценки параметров распределения
Если все варианты 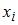 исходного вариационного ряда увеличить на девять единиц, то выборочная дисперсия
исходного вариационного ряда увеличить на девять единиц, то выборочная дисперсия 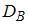 …
…

| не изменится | ||
| увеличится в три раза | |||
| увеличится в 81 раз | |||
| увеличится в девять раз |
Решение:
Для исходного вариационного ряда выборочную дисперсию можем вычислить
по формуле 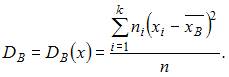
Тогда для нового вариационного ряда 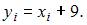
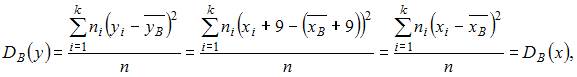
то есть не изменится.
 ЗАДАНИЕ N 8 отправить сообщение разработчикам
ЗАДАНИЕ N 8 отправить сообщение разработчикам
Тема: Системы линейных уравнений
Однородная система 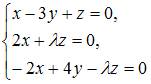 имеет только одно нулевое решение, если
имеет только одно нулевое решение, если 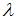 принимает значения не равные …
принимает значения не равные …

| 2 | ||
| – 2 | |||
| 1 | |||
| – 1 |
 ЗАДАНИЕ N 9 отправить сообщение разработчикам
ЗАДАНИЕ N 9 отправить сообщение разработчикам
Тема: Базис и размерность линейного пространства
Дано трехмерное векторное пространства с базисом 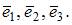 Если векторы
Если векторы 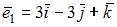 и
и 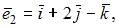 то вектор
то вектор 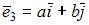 может иметь вид …
может иметь вид …

| 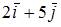
| ||
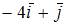
| |||
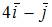
| |||
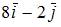
|
 ЗАДАНИЕ N 10 отправить сообщение разработчикам
ЗАДАНИЕ N 10 отправить сообщение разработчикам
Тема: Умножение матриц
Даны матрицы 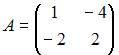 и
и 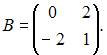 Тогда матрица
Тогда матрица 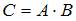 имеет вид …
имеет вид …

| 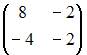
| ||
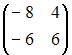
| |||
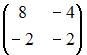
| |||
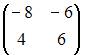
|
 ЗАДАНИЕ N 11 отправить сообщение разработчикам
ЗАДАНИЕ N 11 отправить сообщение разработчикам
Тема: Вычисление определителей
Определитель  равен …
равен …

| 91 | ||
| 97 | |||
| 83 | |||
| 89 |
 ЗАДАНИЕ N 12 отправить сообщение разработчикам
ЗАДАНИЕ N 12 отправить сообщение разработчикам
Тема: Приложения определенного интеграла
Площадь фигуры, изображенной на рисунке
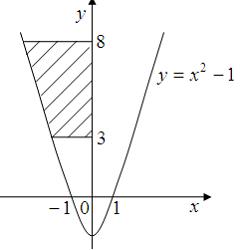
равна …

| 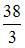
| ||
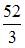
| |||
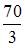
| |||
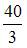
|
Решение:
Площадь данной фигуры можно вычислить по формуле 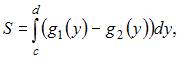 где
где 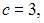
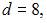
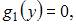
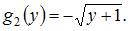 Тогда
Тогда
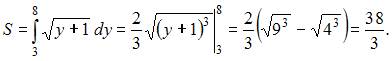
 ЗАДАНИЕ N 13 отправить сообщение разработчикам
ЗАДАНИЕ N 13 отправить сообщение разработчикам
Тема: Непрерывность функции, точки разрыва
Функция 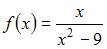 непрерывна на отрезке …
непрерывна на отрезке …

| 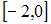
| ||
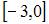
| |||
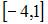
| |||
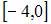
|
 ЗАДАНИЕ N 14 отправить сообщение разработчикам
ЗАДАНИЕ N 14 отправить сообщение разработчикам
Тема: Основные методы интегрирования
Множество первообразных функции 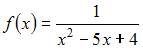 имеет вид …
имеет вид …

| 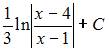
| ||
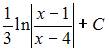
| |||
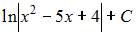
| |||
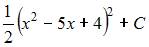
|
 ЗАДАНИЕ N 15 отправить сообщение разработчикам
ЗАДАНИЕ N 15 отправить сообщение разработчикам
Тема: Дифференциальное исчисление ФНП
Частная производная второго порядка 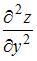 функции
функции 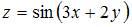 имеет вид …
имеет вид …

| 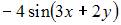
| ||
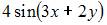
| |||
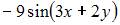
| |||
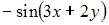
|
 ЗАДАНИЕ N 16 отправить сообщение разработчикам
ЗАДАНИЕ N 16 отправить сообщение разработчикам
Тема: Системы линейных уравнений с комплексными коэффициентами
Решение системы уравнений 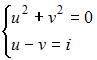 имеет вид …
имеет вид …

| 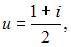 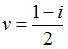
| ||
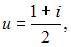 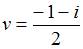
| |||
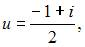 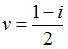
| |||
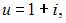 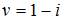
|
Решение:
Выразим 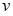 из второго уравнения
из второго уравнения 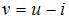 и подставим в первое уравнение системы
и подставим в первое уравнение системы 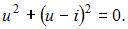 Получим квадратное уравнение
Получим квадратное уравнение 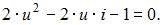 Его решения
Его решения 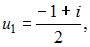
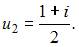 Соответствующие им значения переменной
Соответствующие им значения переменной 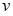 будут равны
будут равны 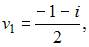
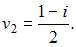 Таким образом, решения системы будут иметь вид:
Таким образом, решения системы будут иметь вид: 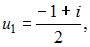
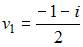 и
и 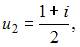
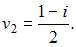
 ЗАДАНИЕ N 17 отправить сообщение разработчикам
ЗАДАНИЕ N 17 отправить сообщение разработчикам
Тема: Дифференцирование функции комплексного переменного
Если 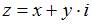 и
и 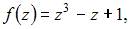 то действительная часть производной этой функции
то действительная часть производной этой функции 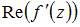 имеет вид …
имеет вид …

| 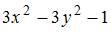
| ||
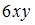
| |||
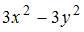
| |||
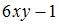
|
Решение:
Производная функции 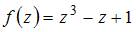 равна
равна 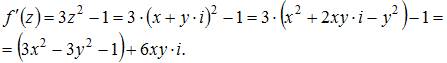
Тогда 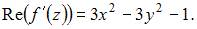
 ЗАДАНИЕ N 18 отправить сообщение разработчикам
ЗАДАНИЕ N 18 отправить сообщение разработчикам
Тема: Комплексные числа и их представление
Комплексное число задано в алгебраической форме 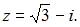 Тогда показательная форма записи сопряженного к нему числа
Тогда показательная форма записи сопряженного к нему числа 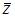 имеет вид …
имеет вид …

| 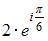
| ||
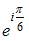
| |||
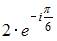
| |||
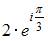
|
Решение:
Если 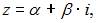 то
то 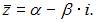 В нашем случае
В нашем случае 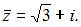 Запись комплексного числа в виде
Запись комплексного числа в виде 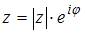 называют показательной формой комплексного числа. Если комплексное число записано в форме
называют показательной формой комплексного числа. Если комплексное число записано в форме 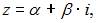 то
то 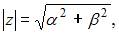 а аргумент
а аргумент 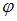 определяется из системы уравнений:
определяется из системы уравнений: 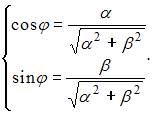 В нашем случае
В нашем случае 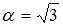 и
и 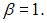
Тогда 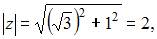
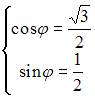
и главное значение аргумента равно 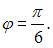 Показательная форма данного комплексного числа имеет вид
Показательная форма данного комплексного числа имеет вид 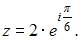
 ЗАДАНИЕ N 19 отправить сообщение разработчикам
ЗАДАНИЕ N 19 отправить сообщение разработчикам
Тема: Область сходимости степенного ряда
Область сходимости степенного ряда 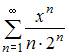 имеет вид …
имеет вид …

| [– 2; 2) | ||
| (– 2; 2) | |||
| (– 2 2] | |||
| [– 2; 2] |
Решение:
Вычислим предварительно радиус сходимости этого ряда по формуле 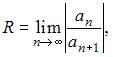 где
где 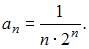 Тогда
Тогда 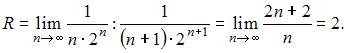 Следовательно, интервал сходимости ряда имеет вид
Следовательно, интервал сходимости ряда имеет вид 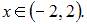
Для того чтобы найти область сходимости степенного ряда, исследуем сходимость ряда в граничных точках.
В точке x= - 2 ряд примет вид 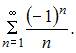 Применим признак сходимости Лейбница, то есть:
Применим признак сходимости Лейбница, то есть:
1) вычислим предел 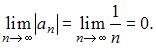
2) для любого натурального 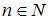 справедливо
справедливо 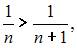
то есть последовательность 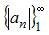 монотонно убывает.
монотонно убывает.
Следовательно, ряд 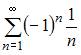 сходится.
сходится.
В точке x=2 ряд примет вид 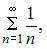 а это расходящийся гармонический ряд.
а это расходящийся гармонический ряд.
Таким образом, область сходимости примет вид 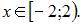
 ЗАДАНИЕ N 20 отправить сообщение разработчикам
ЗАДАНИЕ N 20 отправить сообщение разработчикам
Тема: Сходимость числовых рядов
Расходящимся является числовой ряд …

| 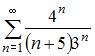
| ||
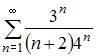
| |||
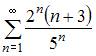
| |||
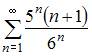
|
 ЗАДАНИЕ N 21 отправить сообщение разработчикам
ЗАДАНИЕ N 21 отправить сообщение разработчикам
Тема: Числовые последовательности
Из числовых последовательностей 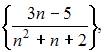
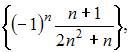
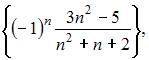
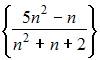 не является сходящейся последовательность …
не является сходящейся последовательность …

| 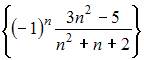
| ||
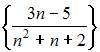
| |||
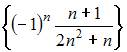
| |||
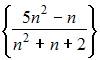
|
 ЗАДАНИЕ N 22 отправить сообщение разработчикам
ЗАДАНИЕ N 22 отправить сообщение разработчикам
Тема: Законы распределения вероятностей дискретных случайных величин
Банк выдал пять кредитов. Вероятность того, что кредит не будет погашен в срок, равна 0,1. Тогда вероятность того, что в срок не будут погашены три кредита, равна …

| 0,0081 | ||
| 0,081 | |||
| 0,06 | |||
| 0,0729 |
 ЗАДАНИЕ N 23 отправить сообщение разработчикам
ЗАДАНИЕ N 23 отправить сообщение разработчикам
Тема: Определение вероятности
В круг радиуса 8 помещен меньший круг радиуса 5. Тогда вероятность того, что точка, наудачу брошенная в больший круг, попадет также и в меньший круг, равна …

| 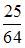
| ||
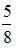
| |||
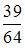
| |||
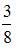
|








