ЗАДАНИЕ N 28 отправить сообщение разработчикам Тема: Статистическое распределение выборки Статистическое распределение выборки имеет вид Тогда значение относительной частоты w4 равно …

| 0,25 | ||
| 0,05 | |||
| 0,26 | |||
| 0,75 |
Решение:
Сумма относительных частот равна единице. Поэтому 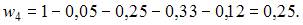
 ЗАДАНИЕ N 29 отправить сообщение разработчикам
ЗАДАНИЕ N 29 отправить сообщение разработчикам
Тема: Точечные оценки параметров распределения
Если все варианты 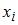 исходного вариационного ряда увеличить в четыре раза, то выборочное среднее
исходного вариационного ряда увеличить в четыре раза, то выборочное среднее 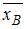 …
…

| увеличится в четыре раза | ||
| увеличится в два раза | |||
| не изменится | |||
| увеличится на четыре единицы |
Решение:
Для исходного вариационного ряда выборочное среднее можем вычислить
по формуле 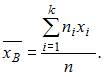
Тогда для нового вариационного ряда 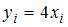
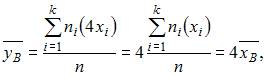
то есть увеличится в четыре раза.
 ЗАДАНИЕ N 30 отправить сообщение разработчикам
ЗАДАНИЕ N 30 отправить сообщение разработчикам
Тема: Интервальные оценки параметров распределения
Точечная оценка математического ожидания нормально распределенного количественного признака равна 12,04. Тогда его интервальная оценка с точностью 1,66 имеет вид …

| (10,38; 13,70) | ||
| (0; 13,70) | |||
| (11,21; 12,87) | |||
| (10,38; 12,04) |
Решение:
Доверительный интервал для оценки математического ожидания нормально распределенного количественного признака можно представить в виде симметричного интервала 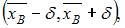 где точечная оценка математического ожидания
где точечная оценка математического ожидания 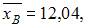 а точность оценки
а точность оценки 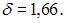
Следовательно, интервальная оценка будет иметь вид (10,38; 13,70).
 ЗАДАНИЕ N 31 отправить сообщение разработчикам
ЗАДАНИЕ N 31 отправить сообщение разработчикам
Тема: Плоскость в пространстве
Уравнение плоскости, проходящей через точки 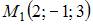 и
и 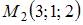 параллельно вектору
параллельно вектору 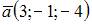 имеет вид …
имеет вид …

| 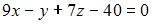
| ||
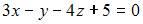
| |||
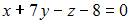
| |||
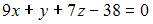
|
Решение:
Рассмотрим некоторую точку 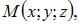 принадлежащую искомой плоскости. Необходимо, чтобы вектора
принадлежащую искомой плоскости. Необходимо, чтобы вектора 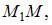
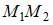 и
и 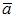 были компланарны. То есть уравнение плоскости, проходящей через точки
были компланарны. То есть уравнение плоскости, проходящей через точки 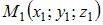 и
и 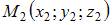 параллельно вектору
параллельно вектору 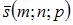 , может быть представлено в следующем виде:
, может быть представлено в следующем виде: 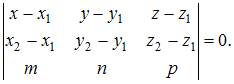
Тогда 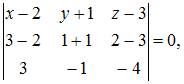 или
или 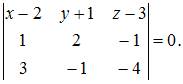
Следовательно, уравнение плоскости примет вид:
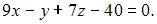
 ЗАДАНИЕ N 32 отправить сообщение разработчикам
ЗАДАНИЕ N 32 отправить сообщение разработчикам
Тема: Прямоугольные координаты на плоскости
Расстояние от точки 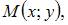 лежащей на оси ординат, до точки
лежащей на оси ординат, до точки 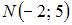 равно 2. Тогда точка
равно 2. Тогда точка 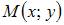 имеет координаты …
имеет координаты …

| 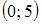
| ||
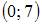
| |||
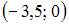
| |||
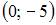
|
Решение:
Так как точка 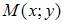 лежит на оси ординат, то ее абсцисса
лежит на оси ординат, то ее абсцисса 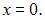 Тогда расстояние между точками
Тогда расстояние между точками 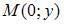 и
и 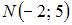 можно определить как
можно определить как 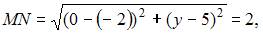 или
или 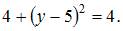 Тогда
Тогда 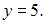
 ЗАДАНИЕ N 33 отправить сообщение разработчикам
ЗАДАНИЕ N 33 отправить сообщение разработчикам
Тема: Поверхности второго порядка
Сфера с центром 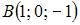 проходит через точку
проходит через точку 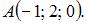 Тогда ее уравнение имеет вид …
Тогда ее уравнение имеет вид …

| 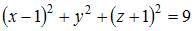
| ||
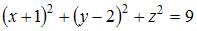
| |||
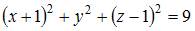
| |||
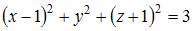
|
Решение:
Уравнение сферы радиуса R с центром в точке 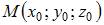 имеет вид
имеет вид 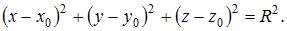
Подставим координаты центра 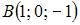 в это уравнение:
в это уравнение:
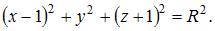
Радиус сферы найдем из условия, что координаты точки 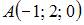 удовлетворяют уравнению сферы:
удовлетворяют уравнению сферы: 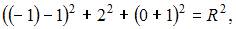 то есть
то есть 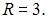
Тогда уравнение сферы примет вид: 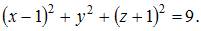
 ЗАДАНИЕ N 34 отправить сообщение разработчикам
ЗАДАНИЕ N 34 отправить сообщение разработчикам
Тема: Прямая на плоскости
Уравнение геометрического места точек, равноудаленных от двух данных точек 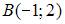 и
и 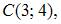 имеет вид …
имеет вид …

| 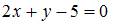
| ||
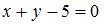
| |||
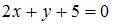
| |||
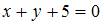
|
 ЗАДАНИЕ N 35 отправить сообщение разработчикам
ЗАДАНИЕ N 35 отправить сообщение разработчикам
Тема: Норма вектора в евклидовом пространстве
Даны векторы 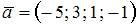 и
и 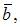 угол между которыми равен
угол между которыми равен 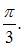 Тогда проекция вектора
Тогда проекция вектора 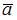 на вектор
на вектор 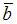 равна …
равна …

| 3 | ||
| – 2 | |||
| 6 | |||
| – 3 |
Решение:
Так как 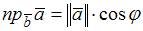 и
и 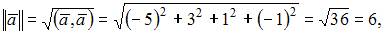 то
то 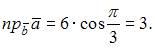
 ЗАДАНИЕ N 36 отправить сообщение разработчикам
ЗАДАНИЕ N 36 отправить сообщение разработчикам
Тема: Векторное произведение векторов
Векторное произведение векторов 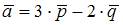 и
и 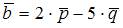 равно …
равно …

| 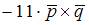
| ||
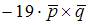
| |||
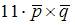
| |||
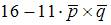
|
Решение:
Вычислим
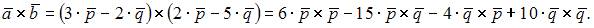
Так как 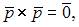
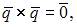
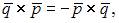 то
то 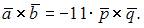
 ЗАДАНИЕ N 37 отправить сообщение разработчикам
ЗАДАНИЕ N 37 отправить сообщение разработчикам
Тема: Градиент скалярного поля
Градиент скалярного поля 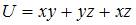 равен нулевому вектору в точке …
равен нулевому вектору в точке …

| (0; 0; 0) | ||
| (– 1; 0; 1) | |||
| (1; 1; 1) | |||
| (0; 1; 1) |
Решение:
Градиент скалярного поля находится по формуле: 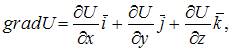 где
где 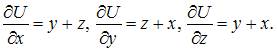 Градиент поля равен нулевому вектору тогда и только тогда, когда
Градиент поля равен нулевому вектору тогда и только тогда, когда 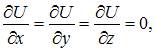 то есть когда
то есть когда 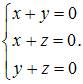
Решив эту систему, получаем единственное решение 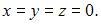
То есть, градиент поля U равен нулевому вектору в точке 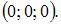
 ЗАДАНИЕ N 38 отправить сообщение разработчикам
ЗАДАНИЕ N 38 отправить сообщение разработчикам
Тема: Сходимость числовых рядов
Даны числовые ряды:
А) 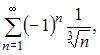
В) 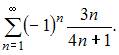
Тогда …

| ряд А) сходится, ряд В) расходится | ||
| ряд А) расходится, ряд В) расходится | |||
| ряд А) сходится, ряд В) сходится | |||
| ряд А) расходится, ряд В) сходится |
Решение:
Для исследования сходимости знакочередующегося ряда 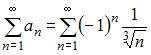 применим признак сходимости Лейбница.
применим признак сходимости Лейбница.
Тогда:
1) вычислим предел 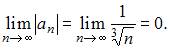
2) для любого натурального 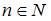 справедливо
справедливо 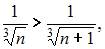
то есть последовательность 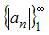 монотонно убывает.
монотонно убывает.
Следовательно, ряд 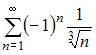 сходится.
сходится.
Ряд 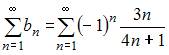 расходится, так как
расходится, так как 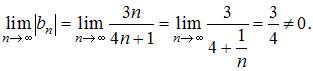
 ЗАДАНИЕ N 39 отправить сообщение разработчикам
ЗАДАНИЕ N 39 отправить сообщение разработчикам
Тема: Числовые последовательности
Общий член числовой последовательности 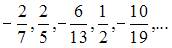 имеет вид …
имеет вид …

| 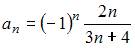
| ||
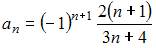
| |||
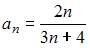
| |||
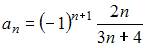
|
Решение:
Если представить данную последовательность в виде 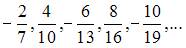 , то легко заметить, что из предложенных ответов правильным является
, то легко заметить, что из предложенных ответов правильным является 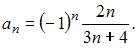
 ЗАДАНИЕ N 40 отправить сообщение разработчикам
ЗАДАНИЕ N 40 отправить сообщение разработчикам
Тема: Область сходимости степенного ряда
Радиус сходимости равен 2,5 для степенного ряда …

| 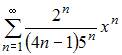
| ||
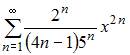
| |||
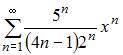
| |||
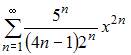
|
Решение:
Радиус сходимости равен 2,5 для степенного ряда 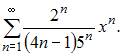 Действительно,
Действительно,
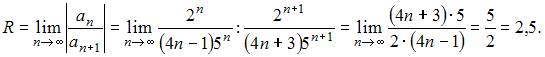
 ЗАДАНИЕ N 41 отправить сообщение разработчикам
ЗАДАНИЕ N 41 отправить сообщение разработчикам
Тема: Умножение матриц
Даны матрицы 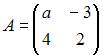 и
и 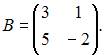 Если матрица
Если матрица 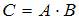 вырожденная, то значение a равно …
вырожденная, то значение a равно …

| – 6 | ||
| 5 | |||
| – 5 | |||
| 0 |
 ЗАДАНИЕ N 42 отправить сообщение разработчикам
ЗАДАНИЕ N 42 отправить сообщение разработчикам
Тема: Вычисление определителей
Определитель 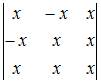 равен …
равен …

| 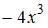
| ||
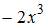
| |||
| 0 | |||
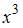
|
Решение:
Определитель третьего порядка можно вычислить, например, разложением по элементам первой строки:
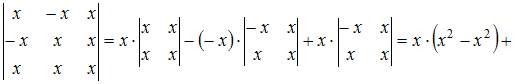
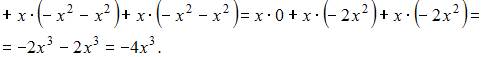
 ЗАДАНИЕ N 43 отправить сообщение разработчикам
ЗАДАНИЕ N 43 отправить сообщение разработчикам
Тема: Базис и размерность линейного пространства
Разложение вектора 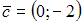 по векторам
по векторам 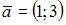 и
и 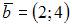 имеет вид …
имеет вид …

| 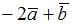
| ||
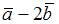
| |||
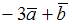
| |||
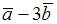
|
Решение:
Разложение вектора 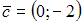 по векторам
по векторам 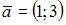 и
и 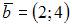 имеет вид
имеет вид 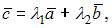 представим это равенство в виде системы из двух уравнений с двумя неизвестными
представим это равенство в виде системы из двух уравнений с двумя неизвестными 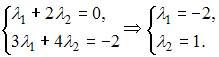
 ЗАДАНИЕ N 44 отправить сообщение разработчикам
ЗАДАНИЕ N 44 отправить сообщение разработчикам
Тема: Системы линейных уравнений
Метод Гаусса для решения систем линейных уравнений заключается …

| в последовательном исключении переменных | ||
| в последовательном исключении свободных членов | |||
| в нахождении обратной матрицы | |||
| в вычислении вспомогательных определителей системы |








