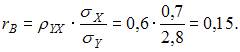ЗАДАНИЕ N 17 отправить сообщение разработчикам Тема: Гармонические колебания Точка совершает гармонические колебания вдоль оси Ox с амплитудой Тогда уравнение этих колебаний может иметь вид …
ЗАДАНИЕ N 1 отправить сообщение разработчикам
Тема: Элементы теории множеств
Даны множества: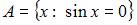 
и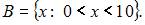 
Тогда число элементов, принадлежащих их пересечению равно …
| 3 |
ЗАДАНИЕ N 2 отправить сообщение разработчикам
Тема: Метрические пространства
Расстояние между точкам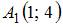и 
и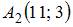 
в метрике 
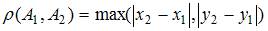, где 
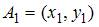и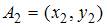 
, равно …
|
| 10 | ||
| 1 | |||
| |||
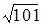
| – 1 |
ЗАДАНИЕ N 3 отправить сообщение разработчикам
Тема: Мера плоского множества
Мера плоского множества, изображенного на рисунке,
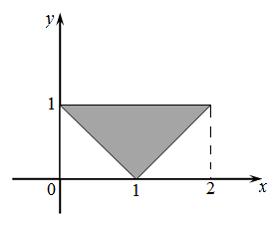
равна …
|
| 1 | ||
| |||
| |||
|
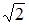
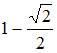
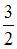
ЗАДАНИЕ N 4 отправить сообщение разработчикам
Тема: Отображение множеств
Образом отрезка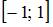 
при отображении y = 2x является …
|
| [0,5; 2] | ||
| [– 2; 2] | |||
| [– 0,5; 2] | |||
|
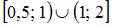
Решение:
Образом множества 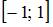при отображении y = 2x являются те точки 
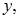в которые при данном отображении попадают точки x из 
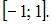В нашем случае это множество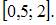 
ЗАДАНИЕ N 5 отправить сообщение разработчикам
Тема: Приложения определенного интеграла
Площадь фигуры, изображенной на рисунке
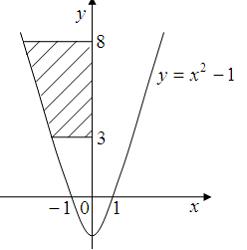
равна …
|
| 
| ||
| |||
| |||
|
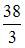
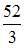
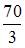
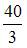
ЗАДАНИЕ N 6 отправить сообщение разработчикам
Тема: Дифференциальное исчисление ФНП
Значение частной производной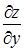 
функции 
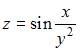в точке 
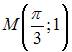равно …
|
| 
| ||
| |||
| |||
|
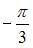
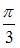
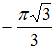
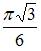
ЗАДАНИЕ N 7 отправить сообщение разработчикам
Тема: Основные методы интегрирования
Множество первообразных функции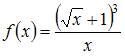 
имеет вид …
|
| 
| ||
| |||
| |||
|
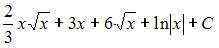
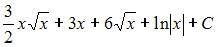
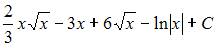
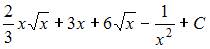
Решение:
Чтобы определить множество первообразных, вычислим неопределенный интеграл от этой функции. Тогда
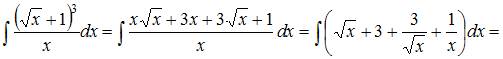
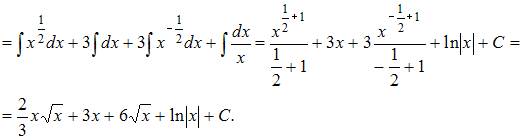
ЗАДАНИЕ N 8 отправить сообщение разработчикам
Тема: Непрерывность функции, точки разрыва
Функция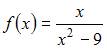 
непрерывна на отрезке …
|
| 
| ||
| |||
| |||
|
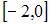
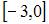
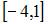
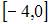
Решение:
Определим точки разрыва данной дробно-рациональной функции, приравняв к нулю знаменатель: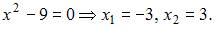 
Тогда данная функция непрерывна при всех x, кроме 
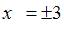. Тогда 
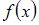будет непрерывна, например, на отрезке 
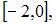так как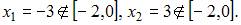 
ЗАДАНИЕ N 9 отправить сообщение разработчикам
Тема: Однородные дифференциальные уравнения
Общий интеграл дифференциального уравнения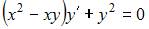 
имеет вид …
|
| 
| ||
| |||
| |||
|
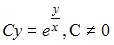
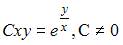
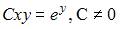
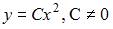
Решение:
Запишем уравнение в виде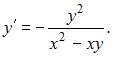 
Сделаем замену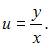 
Тогда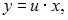 
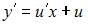и уравнение запишется в виде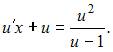 
Разделим переменные: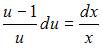 
и проинтегрируем обе части последнего уравнения: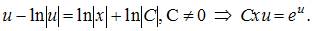 
Сделаем обратную замену: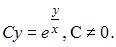 
ЗАДАНИЕ N 10 отправить сообщение разработчикам
Тема: Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
Общий вид частного решения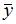 
линейного неоднородного дифференциального уравнения второго порядка 
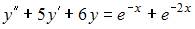будет выглядеть как …
|
| 
| ||
| |||
| |||
|
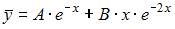
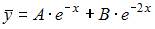
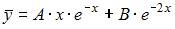
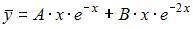
Решение:
Общее решение этого уравнения можно записать в виде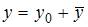 
,
где функция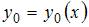 
– общее решение однородного уравнения 
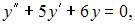а функция 
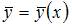– некоторое частное решение исходного неоднородного уравнения.
Для однородного уравнения составим характеристическое уравнение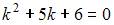 
и найдем его корни: 
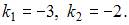Тогда общее решение однородного уравнения будет иметь вид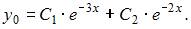 
Поскольку правая часть исходного уравнения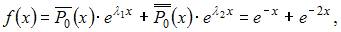 
то имеем уравнение
со специальной правой частью. Так как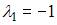 
не является корнем характеристического уравнения, а 
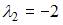– является, то частное решение 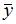неоднородного уравнения будем искать в виде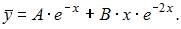 
ЗАДАНИЕ N 11 отправить сообщение разработчикам
Тема: Типы дифференциальных уравнений
Уравнение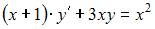 
является …
|
| линейным неоднородным дифференциальным уравнением первого порядка | ||
| однородным относительно x и y дифференциальным уравнением первого порядка | |||
| уравнением Бернулли | |||
| дифференциальным уравнением с разделяющимися переменными |
ЗАДАНИЕ N 12 отправить сообщение разработчикам
Тема: Системы двух линейных дифференциальных уравнений с постоянными коэффициентами
При решении системы дифференциальных уравнений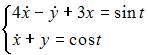 
можно получить уравнение второго порядка вида …
|
| 
| ||
| |||
| |||
|
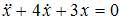
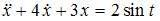
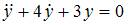
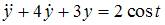
ЗАДАНИЕ N 13 отправить сообщение разработчикам
Тема: Интерполирование функций: интерполяционные полиномы Лагранжа
Функция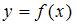 
задана таблично:
В интерполяционном полиноме Лагранжа 2-ой степени с узлами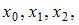 
составленном по этой таблице для приближенного вычисления 
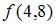при условии 
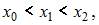значение 
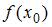не может быть равно …
|
| 12 | ||
| 6 | |||
| 5 | |||
| 8 |
Решение:
Для получения интерполяционного полинома Лагранжа 2-ой степени требуются три узла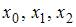 
и значения данной функции в них: 
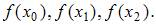Это могут быть любые три точки 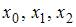из таблицы, удовлетворяющие двум условиям: 
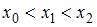и 
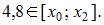Следовательно, в качестве узла 
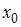нельзя брать 6, 8, 10, 11. Значит, 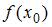не может принимать значения 12, 13, 20, 23.
ЗАДАНИЕ N 14 отправить сообщение разработчикам
Тема: Численные методы решения дифференциальных уравнений и систем
Для задачи Коши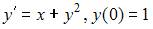 
выполнен один шаг получения приближенного решения методом Эйлера - Коши с шагом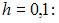 
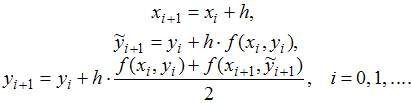
Тогда значение y1, записанное с двумя знаками после запятой, равно …
|
| 1,12 | ||
| 0,9155 | |||
| 1,11 | |||
| 1,1155 |
Решение:
По условию задачи известно, что начальная точка интегральной кривой имеет координаты: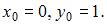 
Правая часть уравнения: 
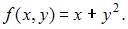Получим следующую точку: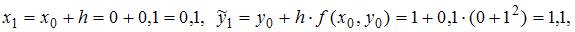 
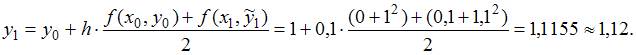
ЗАДАНИЕ N 15 отправить сообщение разработчикам
Тема: Численное дифференцирование и интегрирование
Значение дифференцируемой функции z = f (x, y) в точке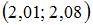 
можно приближенно найти как …
|
| 
| ||
| |||
| |||
|
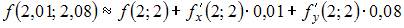
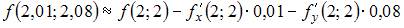
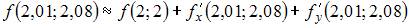
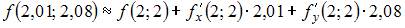
Решение:
Воспользуемся приближенной формулой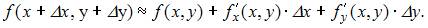 
В нашем случае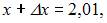 
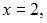
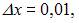
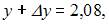
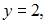
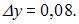
Тогда .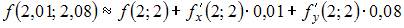
ЗАДАНИЕ N 16 отправить сообщение разработчикам
Тема: Ряд Фурье. Теорема Дирихле
Значение ряда Фурье функции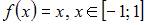 
в точке 
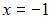равно …
|
| 0 | ||
| – 1 | |||
| 1 | |||
|
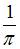
Решение:
Значение ряда Фурье на границах отрезка задания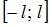 
вычисляется
по формуле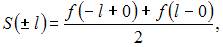 
тогда 
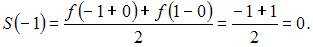
ЗАДАНИЕ N 17 отправить сообщение разработчикам
Тема: Гармонические колебания
Точка совершает гармонические колебания вдоль оси Ox
с амплитудой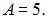 
Тогда уравнение этих колебаний может иметь вид …
|
| 
| ||
| |||
| |||
|
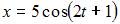
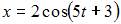
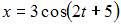
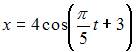
Решение:
Уравнение гармонических колебаний имеет вид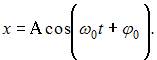 
Тогда амплитуду 
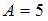имеют колебания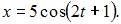 
ЗАДАНИЕ N 18 отправить сообщение разработчикам
Тема: Элементы гармонического анализа
Функцией, ортогональной к функции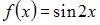 
на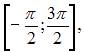 
не является …
|
| 
| ||
| |||
| |||
|
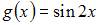
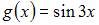
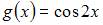
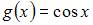
ЗАДАНИЕ N 19 отправить сообщение разработчикам
Тема: Периодические функции
Основной период функции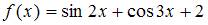 
равен …
|
| 
| ||
| |||
| |||
|
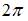
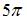
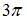
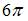
Решение:
Основной период функции sin 2x равен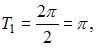 
основной период функции cos 3x равен 
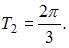Тогда общий основной период должен удовлетворять условию 
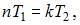то есть 
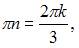или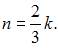 
А это условие выполнятся при минимальных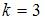 
и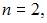 
то есть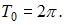 
ЗАДАНИЕ N 20 отправить сообщение разработчикам
Тема: Дифференцирование функции комплексного переменного
Значение производной функции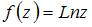 
в точке 
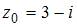равно …
|
| 
| ||
| |||
| |||
|
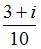
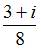
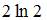
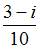
Решение:
Производная функции 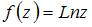имеет вид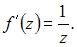 
Тогда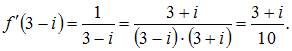 
ЗАДАНИЕ N 21 отправить сообщение разработчикам
Тема: Комплексные числа и их представление
Комплексное число задано в тригонометрической форме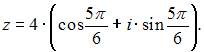 
Тогда алгебраическая форма записи сопряженного к нему числа 
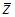имеет вид …
|
| 
| ||
| |||
| |||
|
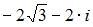
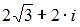
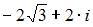
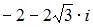
Решение:
Тригонометрическая форма комплексного числа имеет вид: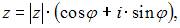 
а алгебраическая –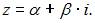 
Тогда для нахождения параметров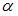 
и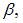 
получим систему: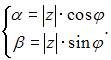 
В нашем случае она примет вид: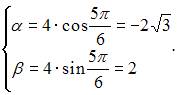 
Следовательно,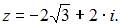 
Если 
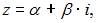то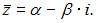 
В нашем случае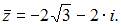 
ЗАДАНИЕ N 22 отправить сообщение разработчикам
Тема: Системы линейных уравнений с комплексными коэффициентами
Есл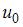и 
и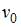 
являются решением системы линейных уравнений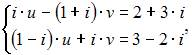 
то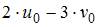 
равно …
|
| 13 | ||
| |||
| |||
|
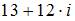
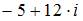
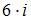
Решение:
Решим систему методом Крамера. Для этого вычислим определитель системы: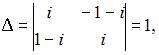 
и вспомогательные определители:
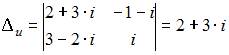
и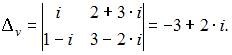 
Тогда по формулам Крамера получим:
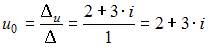и 
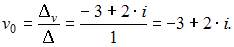
Следовательно,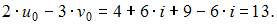 
ЗАДАНИЕ N 23 отправить сообщение разработчикам
Тема: Числовые характеристики случайных величин
Дискретная случайная величина X задана законом распределения вероятностей:
Тогда ее математическое ожидание равно …
|
| 4,6 | ||
| 5,0 | |||
| 3,0 | |||
| 4,9 |
Решение:
Математическое ожидание дискретной случайной величины вычисляется
по формуле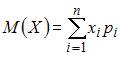 
. Тогда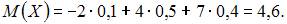 
ЗАДАНИЕ N 24 отправить сообщение разработчикам
Тема: Определение вероятности
Игральная кость бросается два раза. Тогда вероятность того, что сумма выпавших очков не меньше девяти, равна …
|
| 
| ||
| |||
| |||
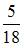
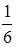
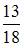
| 0 |
Решение:
Для вычисления события A (сумма выпавших очков будет не меньше девяти) воспользуемся формулой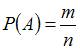 
, где n – общее число возможных элементарных исходов испытания, а m – число элементарных исходов, благоприятствующих появлению события A. В нашем случае возможны 
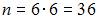элементарных исходов испытания, из которых благоприятствующими являются исходы вида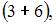 
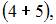
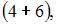
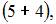
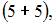
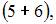
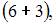
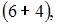
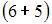и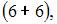 
то есть m = 10. Следовательно,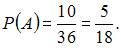 
ЗАДАНИЕ N 25 отправить сообщение разработчикам
Тема: Полная вероятность. Формулы Байеса
В первой урне 6 черных шаров и 4 белых шара. Во второй урне 2 белых и 8 черных шаров. Из наудачу взятой урны вынули один шар, который оказался белым. Тогда вероятность того, что этот шар вынули из первой урны, равна …
|
| 
| ||
| |||
| |||
|
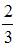
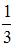
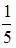
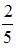
Решение:
Предварительно вычислим вероятность события A (вынутый наудачу шар – белый) по формуле полной вероятности: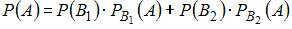 
. Здесь 
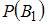– вероятность того,
что шар извлечен из первой урны;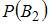 
– вероятность того, что шар извлечен из второй урны; 
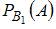– условная вероятность того, что вынутый шар белый, если он извлечен из первой урны; 
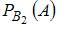– условная вероятность того, что вынутый шар белый, если он извлечен из второй урны.
Тогда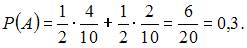 
Теперь вычислим условную вероятность того, что этот шар был извлечен
из первой урны, по формуле Байеса:
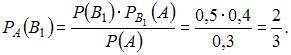
ЗАДАНИЕ N 26 отправить сообщение разработчикам
Тема: Законы распределения вероятностей дискретных случайных величин
Дискретная случайная величина X задана законом распределения вероятностей:
И вероятность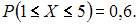 
Тогда значения a, b и c могут быть равны …
|
| a = 0,05, b = 0,30, с = 0,25 | ||
| a = 0,05, b = 0,30 с = 0,35 | |||
| a = 0,05, b = 0,20 с = 0,35 | |||
| a = 0,15, b = 0,30 с = 0,25 |
Решение:
Так как сумма вероятностей возможных значений X равна 1, то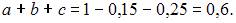 
А так как 
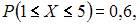то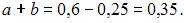 
Следовательно, 
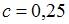, и, например,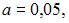 
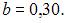
ЗАДАНИЕ N 27 отправить сообщение разработчикам
Тема: Элементы корреляционного анализа
Выборочное уравнение прямой линии регрессии Y на X имеет вид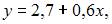 
а выборочные средние квадратические отклонения равны: 
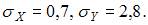Тогда выборочный коэффициент корреляции 
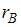равен …
|
| 0,15 | ||
| –2,4 | |||
| 2,4 | |||
| –0,15 |
Решение:
Выборочный коэффициент корреляции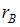 
можно вычислить из соотношения 
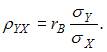Тогда 