ЗАДАНИЕ N 32 отправить сообщение разработчикам Тема: Прямоугольные координаты на плоскости Даны вершины треугольника и Тогда треугольник ABC …
| равнобедренный | ||
| прямоугольный и равнобедренный | |||
| прямоугольный | |||
| равносторонний |
Решение:
Найдем длины сторон треугольника как расстояния между точками A, B и C. Расстояние между двумя точками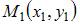 
и 
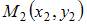находится по формуле 
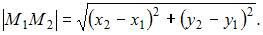Тогда расстояние между точками A и B можно найти как 
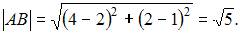Расстояние между точками A и C будет равно 
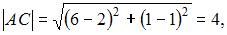аналогично 
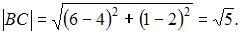Так как 
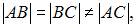то треугольник – равнобедренный.
ЗАДАНИЕ N 33 отправить сообщение разработчикам
Тема: Поверхности второго порядка
Уравнение геометрического места точек, равноудаленных от точки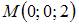 
и от плоскости 
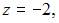имеет вид …
|
| 
| ||
| |||
| |||
|
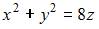
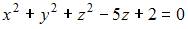
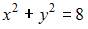
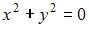
Решение:
Пусть точка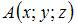 
удовлетворяет заданным условиям. Расстояние от точки A до точки M определяется из соотношения 
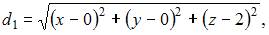а до плоскости 
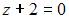как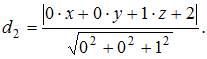 
Так как точка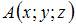 
равноудалена от точки 
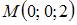и плоскости 
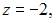то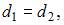 
то есть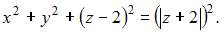 
Тогда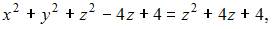 
или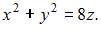 
ЗАДАНИЕ N 34 отправить сообщение разработчикам
Тема: Прямая на плоскости
Прямая линия проходит через точк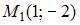и 
и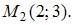 
Тогда она пересекает ось Ox в точке …
|
| 
| ||
| |||
| |||
|
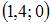
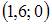
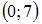
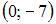
ЗАДАНИЕ N 35 отправить сообщение разработчикам
Тема: Вычисление определителей
Определитель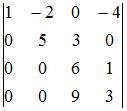 
равен …
|
| 45 | ||
| 135 | |||
| – 45 | |||
| – 135 |
Решение:
Определитель четвертого порядка можно вычислить, например, разложением по элементам первого столбца:
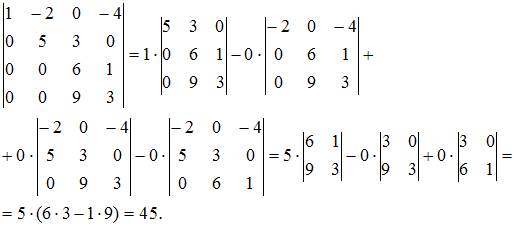
ЗАДАНИЕ N 36 отправить сообщение разработчикам
Тема: Базис и размерность линейного пространства
Даны вектор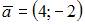 
и матрица 
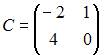перехода от старого базиса к новому. Тогда координаты вектора 
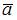в новом базисе имеют вид …
|
| 
| ||
| |||
| |||
|
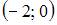
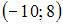
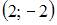
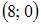
Решение:
Переход от координат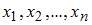 
вектора 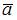относительно старого базиса к координатам 
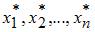относительно нового базиса осуществляется по формуле
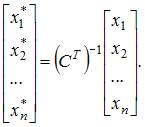Определим транспонированную матрицу 
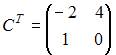и вычислим обратную матрицу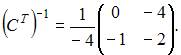 
Следовательно, координаты вектора 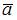в новом базисе будут равны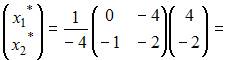 
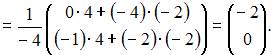
ЗАДАНИЕ N 37 отправить сообщение разработчикам
Тема: Умножение матриц
Матрица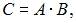 
где 
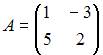и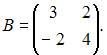 
Тогда элемент 
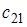равен …
|
| 11 | ||
| – 10 | |||
| – 11 | |||
| 10 |
Решение:
Произведением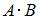 
матрицы A размера 
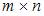на матрицу B размера 
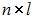называется матрица C размера 
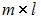, элемент которой 
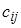равен сумме произведений соответственных элементов i-й строки матрицы A и j-го столбца матрицы B.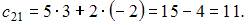 
ЗАДАНИЕ N 38 отправить сообщение разработчикам
Тема: Системы линейных уравнений
Система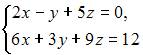 
будет …
|
| совместной и неопределенной | ||
| несовместной и неопределенной | |||
| совместной и определенной | |||
| несовместной и определенной |
Решение:
По методу Гаусса приведем матрицу системы с помощью элементарных преобразований строк к трапецеидальной или треугольной форме. Запишем расширенную матрицу системы и преобразуем ее:
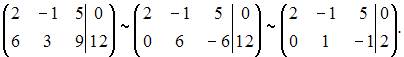Значит, ранг расширенной матрицы равен рангу основной матрицы и система будет совместной. Так как количество переменных больше ранга матрицы, система имеет бесконечное число решений, а значит, является неопределенной.
ЗАДАНИЕ N 39 отправить сообщение разработчикам
Тема: Сходимость числовых рядов
Расходящимся является числовой ряд …
|
| 
| ||
| |||
| |||
|
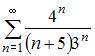
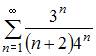
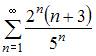
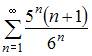
ЗАДАНИЕ N 40 отправить сообщение разработчикам
Тема: Область сходимости степенного ряда
Радиус сходимости равен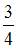 
для степенного ряда …
|
| 
| ||
| |||
| |||
|
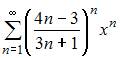
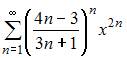
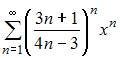
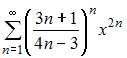
ЗАДАНИЕ N 41 отправить сообщение разработчикам
Тема: Числовые последовательности
Числовая последовательность задана рекуррентным соотношением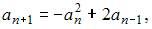 
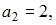
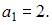Тогда значение выражения 
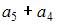равно …
|
| – 12 | ||
| – 20 | |||
| 12 | |||
| – 16 |
ЗАДАНИЕ N 42 отправить сообщение разработчикам
Тема: Численные методы решения дифференциальных уравнений и систем
Методом Эйлера решается задача Коши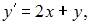 
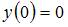с шагом 
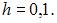Тогда значение искомой функции 
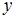в точке 
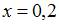будет равно …
|
| 0,02 | ||
| 0,2 | |||
| 0,4 | |||
| 0,04 |
Решение:
Метод Эйлера решения задачи Коши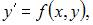 
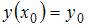
реализуется по следующим формулам:
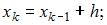
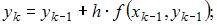
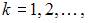
где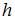 
– шаг расчета (величина изменения аргумент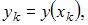а),
а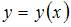 
– искомое решение задачи.
Значения x0 и y0 для значения k = 1 определяются начальным условием задачи Коши.
В нашем случае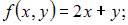 
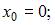
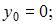
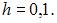
Требуется реализовать два шага (этапа) метода Эйлера, поскольку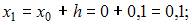 
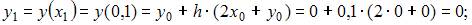
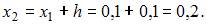
Тогда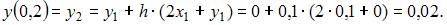 
ЗАДАНИЕ N 43 отправить сообщение разработчикам
Тема: Интерполирование функций: интерполяционные полиномы Лагранжа
Интерполяционный многочлен Лагранжа, составленный по таблице значений функции 
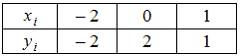
имеет вид …
|
| 
| ||
| |||
| |||
|
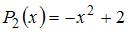
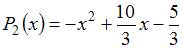
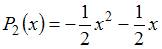
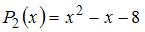
Решение:
Интерполяционный многочлен Лагранжа 2-ой степени для таблицы
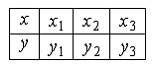
имеет вид:
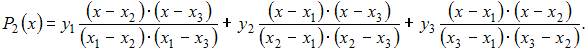
В нашем случае получи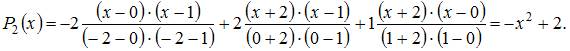м: 
ЗАДАНИЕ N 44 отправить сообщение разработчикам
Тема: Численное дифференцирование и интегрирование
На рисунке
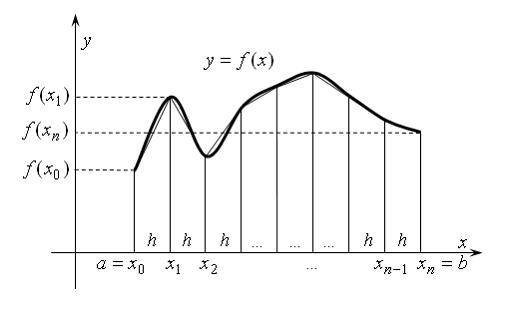
изображена геометрическая интерпретация приближенного вычисления определенного интеграла методом …
|
| трапеций | ||
| правых прямоугольников | |||
| парабол | |||
| левых прямоугольников |