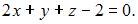ЗАДАНИЕ N 24 отправить сообщение разработчикам Тема: Гармонические колебания Точка совершает гармонические колебания вдоль оси Ox с частотой Тогда уравнение этих колебаний может иметь вид …
| 
| ||
| |||
| |||
|
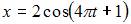
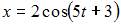
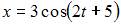
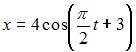
Решение:
Уравнение гармонических колебаний имеет вид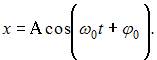 
Угловая частота 
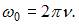Тогда частоту 
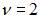имеют колебания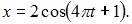 
ЗАДАНИЕ N 25 отправить сообщение разработчикам
Тема: Элементы гармонического анализа
Функцией, ортогональной к функции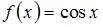 
на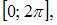 
не является …
|
| 
| ||
| |||
| |||
|
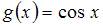
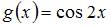
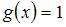
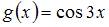
ЗАДАНИЕ N 26 отправить сообщение разработчикам
Тема: Ряд Фурье. Теорема Дирихле
Коэффициент a0 в разложении в ряд Фурье функции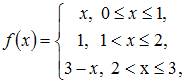 
равен …
|
| 
| ||
| |||
| |||
|
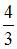
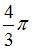
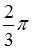
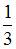
Решение:
Воспользуемся формулой: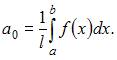 
Тогда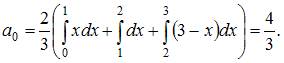 
ЗАДАНИЕ N 27 отправить сообщение разработчикам
Тема: Периодические функции
Период функции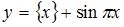 
равен …
|
| 2 | ||
| |||
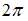
| 1 | |||
|
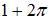
Решение:
Функция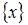 
имеет период 
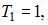функция sin πx – период 
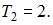Следовательно, исходная функция имеет период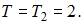 
ЗАДАНИЕ N 28 отправить сообщение разработчикам
Тема: Системы линейных уравнений с комплексными коэффициентами
Есл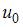и 
и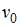 
являются решением системы линейных уравнений 
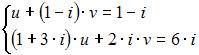, то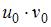 
равно …
|
| 2 | ||
| |||
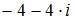
| 32 | |||
| 0 |
Решение:
Решим систему методом Крамера. Для этого вычислим определитель системы:
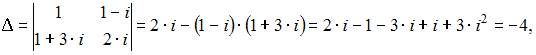
и вспомогательные определител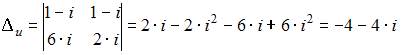и: 
и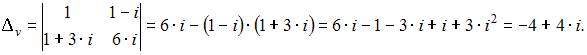 
Тогда по формулам Крамера получим:
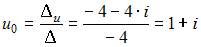и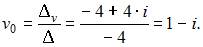 
Следовательно,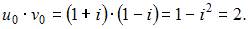 
ЗАДАНИЕ N 29 отправить сообщение разработчикам
Тема: Комплексные числа и их представление
Комплексное число задано в показательной форме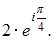 
Тогда алгебраическая форма записи сопряженного к нему числа 
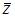имеет вид …
|
| 
| ||
| |||
| |||
|
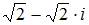
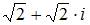
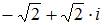
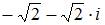
Решение:
Показательная форма комплексного числа имеет вид: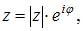 
а алгебраическая –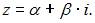 
Так как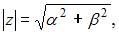 
а главное значение аргумента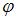 
определяется из системы уравнений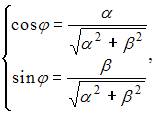 
то для нахождения параметров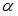 
и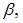 
получим систему: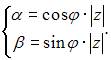 
В нашем случае: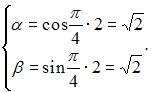 
Следовательно,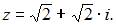 
Если 
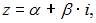то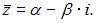 
В нашем случае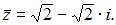 
ЗАДАНИЕ N 30 отправить сообщение разработчикам
Тема: Дифференцирование функции комплексного переменного
Значение производной функции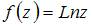 
в точке 
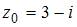равно …
|
| 
| ||
| |||
| |||
|
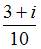
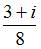
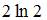
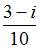
Решение:
Производная функции 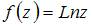имеет вид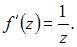 
Тогда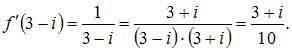 
ЗАДАНИЕ N 31 отправить сообщение разработчикам
Тема: Плоскость в пространстве
Уравнение плоскости, проходящей через точку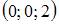 
перпендикулярно плоскостям 
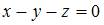и 
и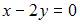меет вид …
|
| 
| ||
| |||
| |||
|
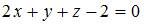
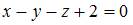
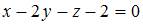
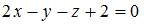
Решение:
Уравнение плоскости, проходящей через точку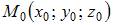 
с нормальным вектором 
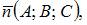имеет вид: 
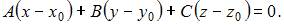В качестве нормального вектора плоскости возьмем векторное произведение нормальных векторов плоскостей 
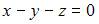и 
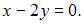Тогда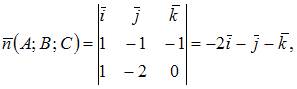 
или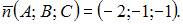 
Подставляя в уравнение плоскости координаты точки 
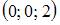и вектора 
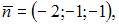получим: 
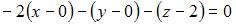или 