ЗАДАНИЕ N 30 отправить сообщение разработчикам Тема: Прямоугольные координаты на плоскости Даны вершины треугольника и Тогда треугольник ABC …
 ЗАДАНИЕ N 1 отправить сообщение разработчикам
ЗАДАНИЕ N 1 отправить сообщение разработчикам
Тема: Мера плоского множества
Мера плоского множества, изображенного на рисунке,
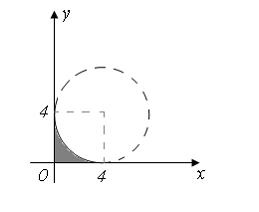
равна …

| 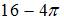
| ||
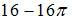
| |||
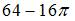
| |||
| 0 |
Решение:
Мера плоского множества равна площади соответствующей фигуры, то есть для ее определения из площади квадрата со стороной 4 нужно вычесть площадь четвертой части круга радиуса 4. Следовательно, мера этого множества равна 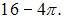
 ЗАДАНИЕ N 2 отправить сообщение разработчикам
ЗАДАНИЕ N 2 отправить сообщение разработчикам
Тема: Метрические пространства
Функция 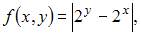 заданная на множестве действительных чисел …
заданная на множестве действительных чисел …

| удовлетворяет всем трем аксиомам метрического пространства | ||
| не удовлетворяет аксиоме тождества | |||
| не удовлетворяет аксиоме симметрии | |||
| не удовлетворяет аксиоме треугольника |
Решение:
Проверим выполнение аксиом метрического пространства:
А) 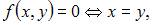
Б) 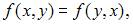
В) 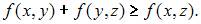
Пусть 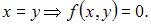
Обратно 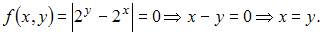
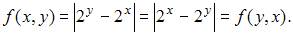
Составим неравенство треугольника для 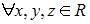
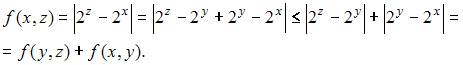
Таким образом, заданная функция удовлетворяет всем аксиомам метрики на множестве действительных чисел.
 ЗАДАНИЕ N 3 отправить сообщение разработчикам
ЗАДАНИЕ N 3 отправить сообщение разработчикам
Тема: Отображение множеств
Образом отрезка 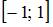 при отображении y = 2x является …
при отображении y = 2x является …

| [0,5; 2] | ||
| [– 2; 2] | |||
| [– 0,5; 2] | |||
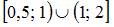
|
Решение:
Образом множества 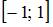 при отображении y = 2x являются те точки
при отображении y = 2x являются те точки 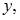 в которые при данном отображении попадают точки x из
в которые при данном отображении попадают точки x из 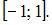 В нашем случае это множество
В нашем случае это множество 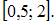
 ЗАДАНИЕ N 4 отправить сообщение разработчикам
ЗАДАНИЕ N 4 отправить сообщение разработчикам
Тема: Элементы теории множеств
Даны множества: 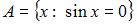 и
и 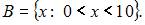 Тогда число элементов, принадлежащих их пересечению равно …
Тогда число элементов, принадлежащих их пересечению равно …
| 3 | |
Решение:
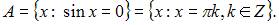 Определим множество
Определим множество 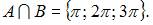 Получили множество, состоящее из трех элементов.
Получили множество, состоящее из трех элементов.
 ЗАДАНИЕ N 5 отправить сообщение разработчикам
ЗАДАНИЕ N 5 отправить сообщение разработчикам
Тема: Векторное произведение векторов
Площадь треугольника, образованного векторами 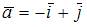 и
и 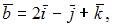 равна …
равна …

| 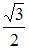
| ||
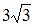
| |||
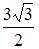
| |||
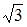
|
Решение:
Площадь S треугольника, построенного на векторах 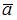 и
и 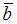 , равна
, равна 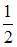 модуля векторного произведения этих векторов, то есть
модуля векторного произведения этих векторов, то есть 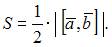 В нашем случае
В нашем случае 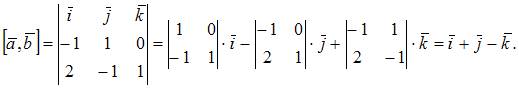
Следовательно, 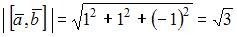 и
и 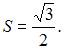
 ЗАДАНИЕ N 6 отправить сообщение разработчикам
ЗАДАНИЕ N 6 отправить сообщение разработчикам
Тема: Градиент скалярного поля
Градиент скалярного поля 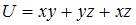 равен нулевому вектору в точке …
равен нулевому вектору в точке …

| (0; 0; 0) | ||
| (– 1; 0; 1) | |||
| (1; 1; 1) | |||
| (0; 1; 1) |
 ЗАДАНИЕ N 7 отправить сообщение разработчикам
ЗАДАНИЕ N 7 отправить сообщение разработчикам
Тема: Норма вектора в евклидовом пространстве
Если 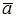 и
и 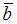 – ортогональные векторы из евклидова пространства со стандартным скалярным произведением, такие что
– ортогональные векторы из евклидова пространства со стандартным скалярным произведением, такие что 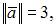
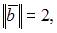 то норма вектора
то норма вектора 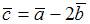 равна …
равна …

| 5 | ||
| 25 | |||
| 1 | |||
| – 1 |
Решение:
Так как 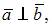 то
то 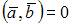 и
и
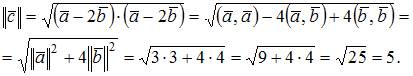
 ЗАДАНИЕ N 8 отправить сообщение разработчикам
ЗАДАНИЕ N 8 отправить сообщение разработчикам
Тема: Элементы корреляционного анализа
Выборочное уравнение прямой линии регрессии X на Y имеет вид 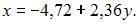 Тогда выборочный коэффициент корреляции может быть равен …
Тогда выборочный коэффициент корреляции может быть равен …

| 0,71 | ||
| –0,50 | |||
| 2,36 | |||
| –2,0 |
Решение:
Значение выборочного коэффициента корреляции, во-первых, принадлежит промежутку 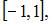 а во-вторых, его знак совпадает со знаком выборочного коэффициента регрессии. Этим условиям удовлетворяет значение 0,71.
а во-вторых, его знак совпадает со знаком выборочного коэффициента регрессии. Этим условиям удовлетворяет значение 0,71.
 ЗАДАНИЕ N 9 отправить сообщение разработчикам
ЗАДАНИЕ N 9 отправить сообщение разработчикам
Тема: Точечные оценки параметров распределения
Если все варианты 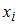 исходного вариационного ряда увеличить на девять единиц, то выборочная дисперсия
исходного вариационного ряда увеличить на девять единиц, то выборочная дисперсия 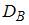 …
…

| не изменится | ||
| увеличится в три раза | |||
| увеличится в 81 раз | |||
| увеличится в девять раз |
 ЗАДАНИЕ N 10 отправить сообщение разработчикам
ЗАДАНИЕ N 10 отправить сообщение разработчикам
Тема: Интервальные оценки параметров распределения
Точечная оценка математического ожидания нормально распределенного количественного признака равна 12,04. Тогда его интервальная оценка с точностью 1,66 имеет вид …

| (10,38; 13,70) | ||
| (0; 13,70) | |||
| (11,21; 12,87) | |||
| (10,38; 12,04) |
 ЗАДАНИЕ N 11 отправить сообщение разработчикам
ЗАДАНИЕ N 11 отправить сообщение разработчикам
Тема: Статистическое распределение выборки
Из генеральной совокупности извлечена выборка объема n = 100:

Тогда относительная частота варианты 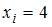 равна …
равна …

| 0,25 | ||
| 0,75 | |||
| 0,24 | |||
| 0,04 |
 ЗАДАНИЕ N 12 отправить сообщение разработчикам
ЗАДАНИЕ N 12 отправить сообщение разработчикам
Тема: Приложения определенного интеграла
Площадь фигуры, изображенной на рисунке
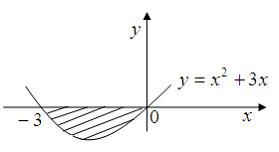
равна …

| 4,5 | ||
| 5,5 | |||
| 10,5 | |||
| 7,5 |
Решение:
Площадь данной фигуры можно вычислить по формуле 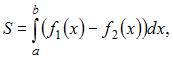 где
где 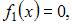
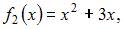
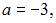
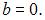 Тогда
Тогда
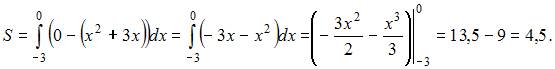
 ЗАДАНИЕ N 13 отправить сообщение разработчикам
ЗАДАНИЕ N 13 отправить сообщение разработчикам
Тема: Основные методы интегрирования
Множество первообразных функции 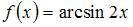 имеет вид …
имеет вид …

| 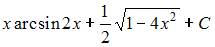
| ||
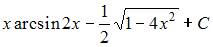
| |||
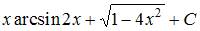
| |||
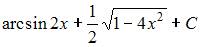
|
 ЗАДАНИЕ N 14 отправить сообщение разработчикам
ЗАДАНИЕ N 14 отправить сообщение разработчикам
Тема: Непрерывность функции, точки разрыва
На отрезке 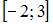 непрерывна функция …
непрерывна функция …

| 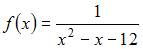
| ||
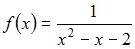
| |||
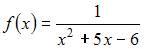
| |||
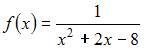
|
 ЗАДАНИЕ N 15 отправить сообщение разработчикам
ЗАДАНИЕ N 15 отправить сообщение разработчикам
Тема: Дифференциальное исчисление ФНП
Частная производная второго порядка 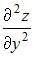 функции
функции 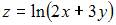 имеет вид …
имеет вид …

| 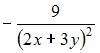
| ||
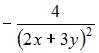
| |||
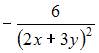
| |||
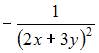
|
 ЗАДАНИЕ N 16 отправить сообщение разработчикам
ЗАДАНИЕ N 16 отправить сообщение разработчикам
Тема: Определение вероятности
Игральная кость бросается два раза. Тогда вероятность того, что сумма выпавших очков – семь, а разность – три, равна …

| 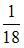
| ||
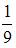
| |||
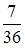
| |||
| 0 |
 ЗАДАНИЕ N 17 отправить сообщение разработчикам
ЗАДАНИЕ N 17 отправить сообщение разработчикам
Тема: Числовые характеристики случайных величин
Дискретная случайная величина X задана законом распределения вероятностей:

Тогда ее математическое ожидание равно …

| 4,6 | ||
| 5,0 | |||
| 3,0 | |||
| 4,9 |
 ЗАДАНИЕ N 18 отправить сообщение разработчикам
ЗАДАНИЕ N 18 отправить сообщение разработчикам
Тема: Законы распределения вероятностей дискретных случайных величин
Среднее число заявок, поступающих на предприятие бытового обслуживания за 1 час равно трем. Тогда вероятность того, что за два часа поступит пять заявок можно вычислить как …

| 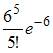
| ||
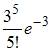
| |||
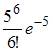
| |||
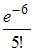
|
 ЗАДАНИЕ N 19 отправить сообщение разработчикам
ЗАДАНИЕ N 19 отправить сообщение разработчикам
Тема: Полная вероятность. Формулы Байеса
Имеются три урны, содержащие по 5 белых и 5 черных шаров, и семь урн, содержащих по 6 белых и 4 черных шара. Из наудачу взятой урны вытаскивается один шар. Тогда вероятность того, что этот шар белый, равна …

| 0,57 | ||
| 0,43 | |||
| 0,55 | |||
| 0,53 |
Решение:
Для вычисления вероятности события A (вынутый наудачу шар – белый) применим формулу полной вероятности: 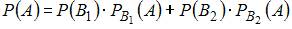 . Здесь
. Здесь 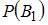 – вероятность того, что шар извлечен из первой серии урн;
– вероятность того, что шар извлечен из первой серии урн; 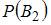 – вероятность того, что шар извлечен из второй серии урн;
– вероятность того, что шар извлечен из второй серии урн; 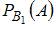 – условная вероятность того, что вынутый шар белый, если из он извлечен из первой серии урн;
– условная вероятность того, что вынутый шар белый, если из он извлечен из первой серии урн; 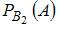 – условная вероятность того, что вынутый шар белый, если из он извлечен из второй серии урн.
– условная вероятность того, что вынутый шар белый, если из он извлечен из второй серии урн.
Тогда 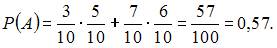
 ЗАДАНИЕ N 20 отправить сообщение разработчикам
ЗАДАНИЕ N 20 отправить сообщение разработчикам
Тема: Системы двух линейных дифференциальных уравнений с постоянными коэффициентами
Функции 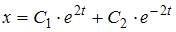 и
и 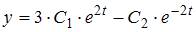 являются решением системы дифференциальных уравнений …
являются решением системы дифференциальных уравнений …

| 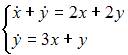
| ||
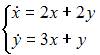
| |||
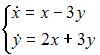
| |||
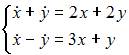
|
Решение:
Найдем 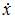 и
и 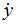 :
: 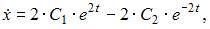
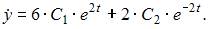 Подставив
Подставив 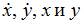 в систему
в систему 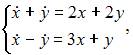 видим, что второе уравнение не обращается в тождество. Подставив
видим, что второе уравнение не обращается в тождество. Подставив 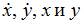 в систему
в систему 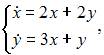 видим, что первое уравнение не обращается в тождество. Подставляя
видим, что первое уравнение не обращается в тождество. Подставляя 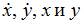 в систему
в систему 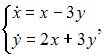 получаем, что оба уравнения не обращаются в тождество.
получаем, что оба уравнения не обращаются в тождество.
При подстановке 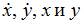 в систему
в систему 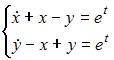 оба уравнения обращаются в тождество. Следовательно, функции
оба уравнения обращаются в тождество. Следовательно, функции 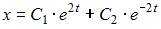 и
и 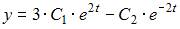 являются решением системы дифференциальных уравнений
являются решением системы дифференциальных уравнений 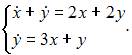
 ЗАДАНИЕ N 21 отправить сообщение разработчикам
ЗАДАНИЕ N 21 отправить сообщение разработчикам
Тема: Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
Общее решение линейного неоднородного дифференциального уравнения второго порядка 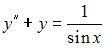 имеет вид …
имеет вид …

| 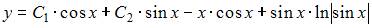
| ||
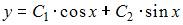
| |||
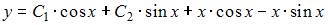
| |||
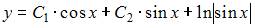
|
Решение:
Составим характеристическое уравнение 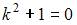 и решим его:
и решим его: 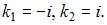 Тогда общее решение исходного уравнения примет вид:
Тогда общее решение исходного уравнения примет вид: 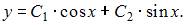 Так как правая часть уравнения не является специальной, будем искать решение методом вариации произвольных постоянных. Так как два линейно независимых частных решения однородного уравнения
Так как правая часть уравнения не является специальной, будем искать решение методом вариации произвольных постоянных. Так как два линейно независимых частных решения однородного уравнения 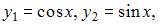 то общее решение неоднородного уравнения будем искать в виде
то общее решение неоднородного уравнения будем искать в виде 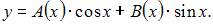 Для нахождения функций
Для нахождения функций 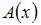 и
и 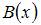
составим систему 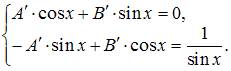 Тогда
Тогда 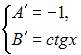 и
и 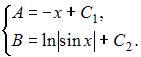 Следовательно,
Следовательно, 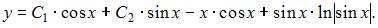
 ЗАДАНИЕ N 22 отправить сообщение разработчикам
ЗАДАНИЕ N 22 отправить сообщение разработчикам
Тема: Типы дифференциальных уравнений
Уравнение 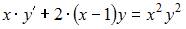 является …
является …

| уравнением Бернулли | ||
| линейным дифференциальным уравнением первого порядка | |||
| дифференциальным уравнением с разделяющимися переменными | |||
| однородным относительно x и y дифференциальным уравнением первого порядка |
Решение:
Уравнение 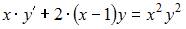 можно представить в виде
можно представить в виде 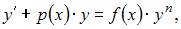 где
где 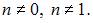
Действительно, 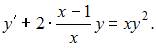 Поэтому данное уравнение является уравнением Бернулли.
Поэтому данное уравнение является уравнением Бернулли.
 ЗАДАНИЕ N 23 отправить сообщение разработчикам
ЗАДАНИЕ N 23 отправить сообщение разработчикам
Тема: Однородные дифференциальные уравнения
Интегральные кривые уравнения 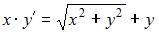 имеют вид …
имеют вид …

| 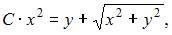 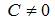
| ||
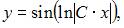 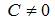
| |||
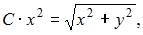 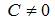
| |||
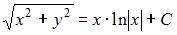
|
 ЗАДАНИЕ N 24 отправить сообщение разработчикам
ЗАДАНИЕ N 24 отправить сообщение разработчикам
Тема: Сходимость числовых рядов
Даны числовые ряды:
А) 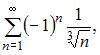
В) 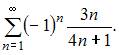
Тогда …

| ряд А) сходится, ряд В) расходится | ||
| ряд А) расходится, ряд В) расходится | |||
| ряд А) сходится, ряд В) сходится | |||
| ряд А) расходится, ряд В) сходится |
 ЗАДАНИЕ N 25 отправить сообщение разработчикам
ЗАДАНИЕ N 25 отправить сообщение разработчикам
Тема: Область сходимости степенного ряда
Интервал сходимости степенного ряда 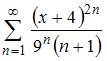 имеет вид …
имеет вид …

| (– 7; – 1) | ||
| (– 13; 5) | |||
| (– 9; 9) | |||
| (– 3; 3) |
 ЗАДАНИЕ N 26 отправить сообщение разработчикам
ЗАДАНИЕ N 26 отправить сообщение разработчикам
Тема: Числовые последовательности
Из числовых последовательностей 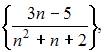
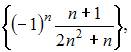
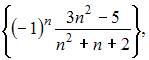
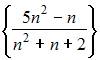 не является сходящейся последовательность …
не является сходящейся последовательность …

| 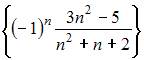
| ||
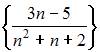
| |||
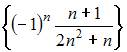
| |||
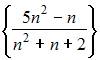
|
 ЗАДАНИЕ N 27 отправить сообщение разработчикам
ЗАДАНИЕ N 27 отправить сообщение разработчикам
Тема: Поверхности второго порядка
Сфера с центром 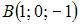 проходит через точку
проходит через точку 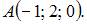 Тогда ее уравнение имеет вид …
Тогда ее уравнение имеет вид …

| 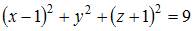
| ||
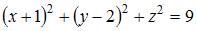
| |||
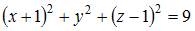
| |||
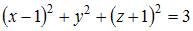
|
 ЗАДАНИЕ N 28 отправить сообщение разработчикам
ЗАДАНИЕ N 28 отправить сообщение разработчикам
Тема: Прямая на плоскости
Прямая проходит через точку 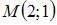 перпендикулярно прямой
перпендикулярно прямой 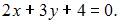 Тогда общее уравнение этой прямой имеет вид …
Тогда общее уравнение этой прямой имеет вид …

| 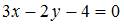
| ||
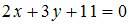
| |||
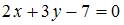
| |||
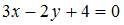
|
 ЗАДАНИЕ N 29 отправить сообщение разработчикам
ЗАДАНИЕ N 29 отправить сообщение разработчикам
Тема: Плоскость в пространстве
Общее уравнение плоскости, проходящей через точку 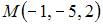 перпендикулярно прямой
перпендикулярно прямой 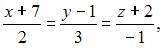 имеет вид …
имеет вид …

| 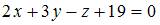
| ||
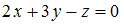
| |||
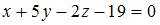
| |||
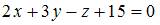
|
 ЗАДАНИЕ N 30 отправить сообщение разработчикам
ЗАДАНИЕ N 30 отправить сообщение разработчикам
Тема: Прямоугольные координаты на плоскости
Даны вершины треугольника 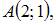
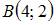 и
и 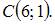
Тогда треугольник ABC …

| равнобедренный | ||
| прямоугольный и равнобедренный | |||
| прямоугольный | |||
| равносторонний |
 ЗАДАНИЕ N 31 отправить сообщение разработчикам
ЗАДАНИЕ N 31 отправить сообщение разработчикам
Тема: Ряд Фурье. Теорема Дирихле
Коэффициент a0 в разложении в ряд Фурье функции 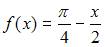
в ряд косинусов на отрезке 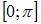 равен …
равен …

| 0 | ||
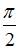
| |||
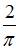
| |||
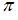
|
Решение:
Воспользуемся формулой: 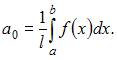
Тогда 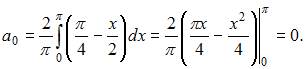
 ЗАДАНИЕ N 32 отправить сообщение разработчикам
ЗАДАНИЕ N 32 отправить сообщение разработчикам
Тема: Гармонические колебания
Модуль ускорения точки, совершающей гармонические колебания, с амплитудой 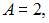 угловой частотой
угловой частотой 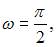 и начальной фазой
и начальной фазой 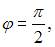
в момент времени 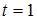 равен …
равен …

| 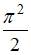
| ||
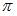
| |||
| 2 | |||
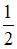
|
 ЗАДАНИЕ N 33 отправить сообщение разработчикам
ЗАДАНИЕ N 33 отправить сообщение разработчикам
Тема: Периодические функции
Наименьший положительный период функции 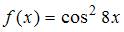 равен …
равен …

| 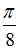
| ||
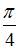
| |||
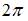
| |||
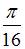
|
Решение:
Представим функцию в виде 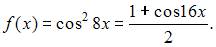 Период данной функции совпадает с периодом функции cos 16x и равен
Период данной функции совпадает с периодом функции cos 16x и равен 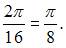
 ЗАДАНИЕ N 34 отправить сообщение разработчикам
ЗАДАНИЕ N 34 отправить сообщение разработчикам
Тема: Элементы гармонического анализа
Функцией, ортогональной к функции 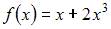
на 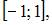 является …
является …

| 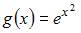
| ||
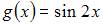
| |||
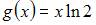
| |||
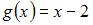
|
Решение:
Функции 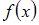 и
и 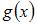 называются ортогональными на
называются ортогональными на 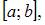
если 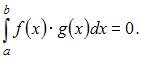 Функция
Функция 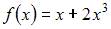 на
на 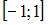 является нечетной, поэтому функция
является нечетной, поэтому функция  в данной задаче должна быть четной, так как тогда произведение
в данной задаче должна быть четной, так как тогда произведение 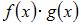 будет нечетной функцией,
будет нечетной функцией,
а интеграл от нечетной функции по симметричному интервалу
равен нулю. Проверим функции на четность:
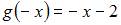 – функция общего вида;
– функция общего вида;
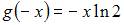 – нечетная функция;
– нечетная функция;
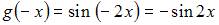 – нечетная функция;
– нечетная функция;
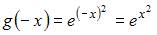 – четная функция.
– четная функция.
Тогда функцией, ортогональной к функции 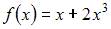
на 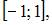 может служить функция
может служить функция 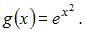
 ЗАДАНИЕ N 35 отправить сообщение разработчикам
ЗАДАНИЕ N 35 отправить сообщение разработчикам
Тема: Базис и размерность линейного пространства
Совокупность векторов 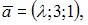
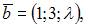
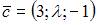 можно принять за базис трехмерного линейного пространства, если
можно принять за базис трехмерного линейного пространства, если 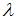 равно …
равно …

| – 5 | ||
| 2 | |||
| 1 | |||
| – 3 |
Решение:
Совокупность линейно независимых векторов называется базисом линейного этого пространства. Значит, совокупность 3 векторов является базисом, если вектора линейно независимы, то есть определитель, составленный из координат этих векторов, не равен нулю. Составим определитель для данной совокупности векторов
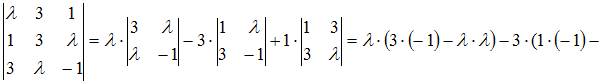
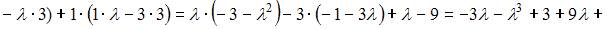
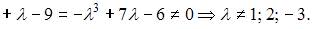
Этому условию удовлетворяет, например, 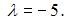
 ЗАДАНИЕ N 36 отправить сообщение разработчикам
ЗАДАНИЕ N 36 отправить сообщение разработчикам
Тема: Умножение матриц
Даны матрицы 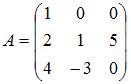 и
и 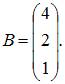 Тогда матрица
Тогда матрица 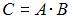 имеет вид …
имеет вид …

| 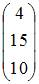
| ||
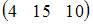
| |||

| |||
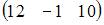
|
 ЗАДАНИЕ N 37 отправить сообщение разработчикам
ЗАДАНИЕ N 37 отправить сообщение разработчикам
Тема: Вычисление определителей
Определитель 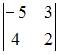 равен …
равен …

| – 22 | ||
| 2 | |||
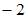
| |||
| 22 |
 ЗАДАНИЕ N 38 отправить сообщение разработчикам
ЗАДАНИЕ N 38 отправить сообщение разработчикам
Тема: Системы линейных уравнений
Система 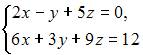 будет …
будет …

| совместной и неопределенной | ||
| несовместной и неопределенной | |||
| совместной и определенной | |||
| несовместной и определенной |
Решение:
По методу Гаусса приведем матрицу системы с помощью элементарных преобразований строк к трапецеидальной или треугольной форме. Запишем расширенную матрицу системы и преобразуем ее:
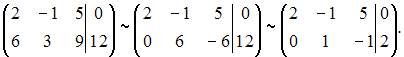 Значит, ранг расширенной матрицы равен рангу основной матрицы и система будет совместной. Так как количество переменных больше ранга матрицы, система имеет бесконечное число решений, а значит, является неопределенной.
Значит, ранг расширенной матрицы равен рангу основной матрицы и система будет совместной. Так как количество переменных больше ранга матрицы, система имеет бесконечное число решений, а значит, является неопределенной.








