ЗАДАНИЕ N 22 отправить сообщение разработчикам Тема: Прямая на плоскости В треугольнике с вершинами уравнение высоты, проведенной из вершины C, имеет вид …
| 
| ||
| |||
| |||
|
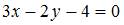
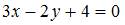
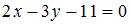
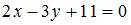
ЗАДАНИЕ N 23 отправить сообщение разработчикам
Тема: Плоскость в пространстве
Уравнение плоскости, проходящей через точк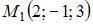и 
и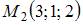 
параллельно вектору 
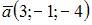имеет вид …
|
| 
| ||
| |||
| |||
|
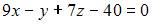
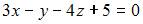
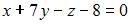
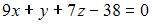
ЗАДАНИЕ N 24 отправить сообщение разработчикам
Тема: Гармонические колебания
Точка совершает гармонические колебания вдоль оси Ox с начальной фазой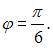 
Тогда уравнение этих колебаний может иметь вид …
|
| 
| ||
| |||
| |||
|
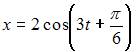
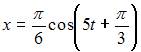
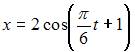
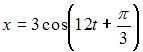
ЗАДАНИЕ N 25 отправить сообщение разработчикам
Тема: Ряд Фурье. Теорема Дирихле
Коэффициент a0 в разложении в ряд Фурье функции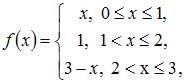 
равен …
|
| 
| ||
| |||
| |||
|
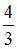
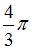
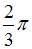
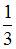
Решение:
Воспользуемся формулой: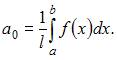 
Тогда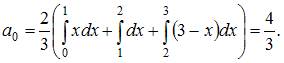 
ЗАДАНИЕ N 26 отправить сообщение разработчикам
Тема: Элементы гармонического анализа
Разложение функции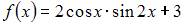 
на гармоники имеет вид …
|
| 
| ||
| |||
| |||
|
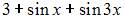
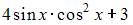
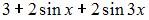
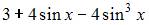
ЗАДАНИЕ N 27 отправить сообщение разработчикам
Тема: Периодические функции
Период функции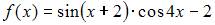 
равен …
|
| 
| ||
| |||
| |||
|
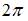
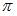
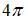
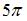
ЗАДАНИЕ N 28 отправить сообщение разработчикам
Тема: Численные методы решения дифференциальных уравнений и систем
На рисунке изображена интегральная кривая, являющаяся решением задачи Коши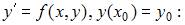 
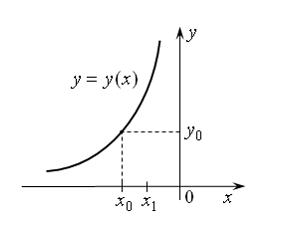
Выполнен один шаг метода Эйлера с шагом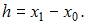 
Тогда точка 
…
|
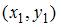| лежит ниже интегральной кривой | ||
| лежит выше интегральной кривой | |||
| лежит на интегральной кривой | |||
| может лежать как ниже, так и выше интегральной кривой |
ЗАДАНИЕ N 29 отправить сообщение разработчикам
Тема: Интерполирование функций: интерполяционные полиномы Лагранжа
Функция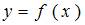 
представлена таблицей
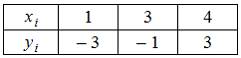
Тогда значение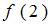 
, вычисленное с помощью интерполяционного многочлена Лагранжа, равно …
|
| – 3 | ||
| 14 | |||
| |||
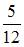
| – 8 |
ЗАДАНИЕ N 30 отправить сообщение разработчикам
Тема: Численное дифференцирование и интегрирование
Метод трапеций дает приближенное значение интеграла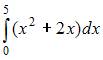 
…
|
| с избытком | ||
| с недостатком | |||
| точно | |||
| про которое ничего определенного сказать нельзя |
Решение:
Геометрическая интерпретация метода трапеций дана на рисунке:
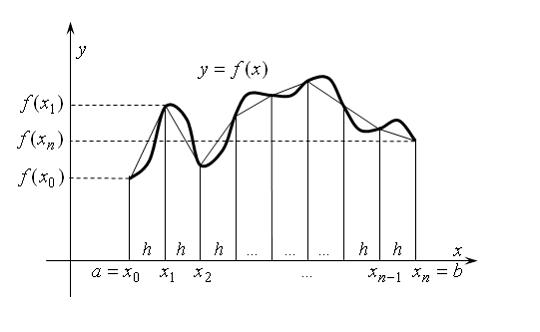
Если подынтегральная функция на частичном отрезке выпукла вверх, то маленькая криволинейная трапеция целиком содержит обычную трапецию, если вниз, то наоборот. В данном случае вторая производная подынтегральной функции положительна: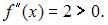 
Значит, на всем отрезке интегрирования и на любом частичном отрезке подынтегральная функция выпукла вниз, то есть приближенное значение интеграла получено
с избытком.
ЗАДАНИЕ N 31 отправить сообщение разработчикам
Тема: Мера плоского множества
Плоская мера множества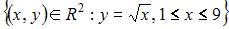 
равна …
|
| 0 | ||
| 32 | |||
| 8 | |||
| 18 |
Решение:
Множество 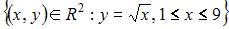задает дугу кривой, ее плоская мера равна нулю.
ЗАДАНИЕ N 32 отправить сообщение разработчикам
Тема: Метрические пространства
Расстояние между точкам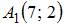и 
и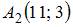 
в метрике 
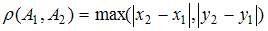, где 
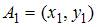и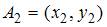 
, равно …
|
| 4 | ||
| 2 | |||
| |||
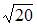
| 0 |
ЗАДАНИЕ N 33 отправить сообщение разработчикам
Тема: Элементы теории множеств
Даны три множества: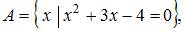 
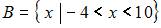и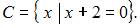 
Тогда число элементов множества 
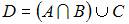равно …
| 2 | |
Решение:
Определим множество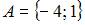 
и выполним операцию пересечения 
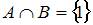, объединим полученное множество с множеством 
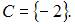В результате получится множество 
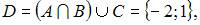состоящее из двух элементов.
ЗАДАНИЕ N 34 отправить сообщение разработчикам
Тема: Отображение множеств
Прообразом множества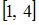 
при отображении y=x2 является …
|
| 
| ||
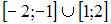
| [1; 2] | |||
| [1; 16] | |||
|
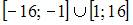
Решение:
Прообразом множества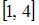 
при отображении y=x2 являются те точки x, которые при данном отображении попадают в 
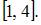В нашем случае это множество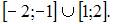 
ЗАДАНИЕ N 35 отправить сообщение разработчикам
Тема: Статистическое распределение выборки
Из генеральной совокупности извлечена выборка объема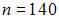 
:
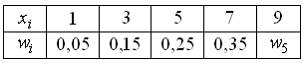
Тогда частота варианты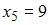 
в выборке равна …
|
| 28 | ||
| 63 | |||
| 42 | |||
| 35 |
ЗАДАНИЕ N 36 отправить сообщение разработчикам
Тема: Точечные оценки параметров распределения
Если все варианты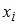 
исходного вариационного ряда увеличить на девять единиц, то выборочная дисперсия 
…
|
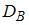| не изменится | ||
| увеличится в три раза | |||
| увеличится в 81 раз | |||
| увеличится в девять раз |
Решение:
Для исходного вариационного ряда выборочную дисперсию можем вычислить
по формуле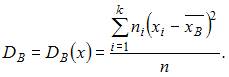 
Тогда для нового вариационного ряда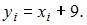 
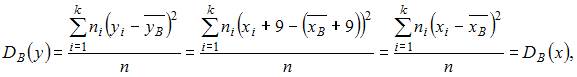
то есть не изменится.
ЗАДАНИЕ N 37 отправить сообщение разработчикам
Тема: Элементы корреляционного анализа
Выборочное уравнение прямой линии регрессии X на Y имеет вид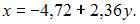 
Тогда выборочный коэффициент корреляции может быть равен …
|
| 0,71 | ||
| –0,50 | |||
| 2,36 | |||
| –2,0 |
ЗАДАНИЕ N 38 отправить сообщение разработчикам
Тема: Интервальные оценки параметров распределения
Точечная оценка среднего квадратического отклонения нормально распределенного количественного признака равна 3,5. Тогда его интервальная оценка может иметь вид …
|
| (0; 8,33) | ||
| (3,5; 8,33) | |||
| (0; 3,5) | |||
| (–1,33; 8,33) |
Решение:
Интервальной оценкой среднего квадратического отклонения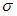 
нормально распределенного количественного признака служит доверительный интервал
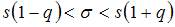при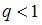 
ил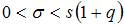и 
при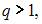 
где q находят по соответствующей таблице приложений.
Этому определению удовлетворяет интервал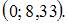 
ЗАДАНИЕ N 39 отправить сообщение разработчикам
Тема: Норма вектора в евклидовом пространстве
В евклидовом пространстве со стандартным скалярным произведением норма вектора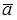 
равна 2, норма вектора 
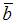равна 1, их скалярное произведение равно 
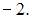Тогда норма вектора 
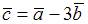равна …
|
| 5 | ||
| – 1 | |||
| 1 | |||
| 25 |
Решение:
Так как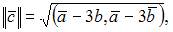 
то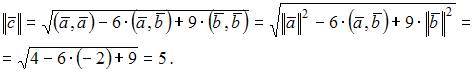 
ЗАДАНИЕ N 40 отправить сообщение разработчикам
Тема: Градиент скалярного поля
Градиент скалярного поля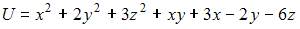 
равен нулевому вектору в точке …
|
| (– 2; 1; 1) | ||
| (1; 0; 1) | |||
| (0; 0; 0) | |||
| (2; – 1; 0) |
ЗАДАНИЕ N 41 отправить сообщение разработчикам
Тема: Векторное произведение векторов
Даны два вектора: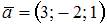 
и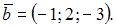 
Тогда вектор 
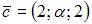будет перпендикулярен и вектору 
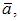и вектору 
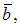при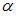 
равном …
|
| 4 | ||
| – 2 | |||
| – 4 | |||
|
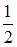
Решение:
Вектор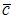 
, перпендикулярный и вектору 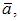и вектору 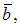можно найти как результат векторного произведения векторов 
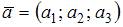и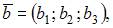 
заданных своими координатами:
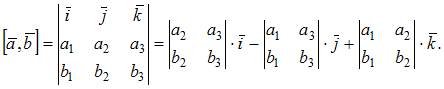
В нашем случае
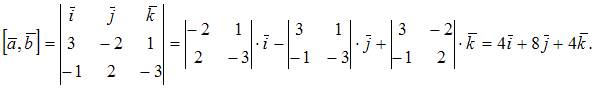
Вектора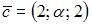 
и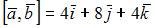 
должны быть коллинеарны. То есть 
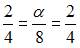и, следовательно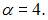 
ЗАДАНИЕ N 42 отправить сообщение разработчикам
Тема: Комплексные числа и их представление
Показательная форма записи комплексного числа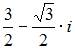 
имеет вид …
|
| 
| ||
| |||
| |||
|
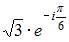
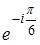
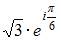
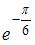
ЗАДАНИЕ N 43 отправить сообщение разработчикам
Тема: Дифференцирование функции комплексного переменного
Если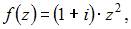 
то 
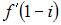равно …
|
| 4 | ||
| 0 | |||
| |||
|
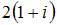
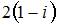
ЗАДАНИЕ N 44 отправить сообщение разработчикам
Тема: Системы линейных уравнений с комплексными коэффициентами
Есл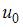и 
и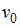 
являются решением системы линейных уравнений 
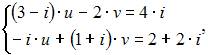то 
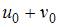равно …
|
| 
| ||
| |||
| |||
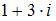
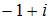
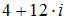
| 4 |
Решение:
Решим систему методом Крамера. Для этого вычислим определитель системы: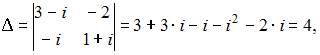 
и вспомогательные определители:
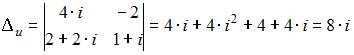
и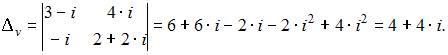 
Тогда по формулам Крамера получим:
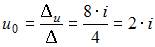и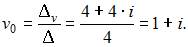 
Следовательно, 