Уравнения (8.1) носят названия уравнений состояния, первое из которых будем называть уравнением входа, а второе – уравнением выхода.

Дата: 2025-05-01; Просмотры: 4

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Уравнения (8.1) описывают динамику нелинейной нестационарной непрерывной системы с сосредоточенными параметрами. Если 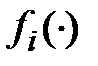, 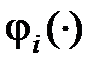в явном виде не зависят от времени t, то имеем соответствующую модель стационарной системы.

Если в некоторой области изменения переменных функции 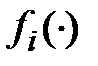, 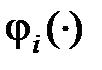являются линейными, то уравнения (8.1) превращаются в линейные уравнения состояния

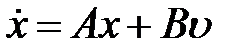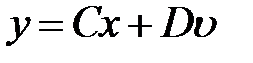, , (8.2)

где А, В, C, D – соответственно матрицы размерностей , , , .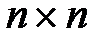

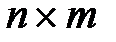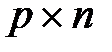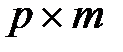Если коэффициенты всех матриц не зависят в явном виде от времени,
то имеем модель линейной стационарной системы. Если хотя бы один из
коэффициентов этих матриц в явном виде зависит от t, то модель будет
нестационарной.

Для физически реализуемых систем всегда D = 0 (здесь и далее равенство матрицы нулю подразумевает равенство нулевой матрице) и чаще всего рассматриваются уравнения состояния вида

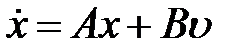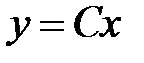, . (8.3)

Матрица А называется основной матрицей системы, В – матрицей входа,
С – матрицей выхода, D – матрицей связи.

В данном разделе будем рассматривать только линейные стационарные системы, описываемые уравнениями (8.2), (8.3).

Отметим ряд дополнительных моментов, касающихся приведенных моделей систем:

1. Для полного описания поведения системы всегда требуется задать ее начальное состояние в некоторый момент времени (чаще всего нулевой). Это соответствует заданию начальных условий для дифференциальных уравнений, входящих в (8.1)–(8.3). Итак, в (8.1)–(8.3) всегда подразумевается задание x(0).Чаще всего .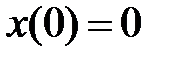

2. Элементы матриц А, В, С, D и векторов 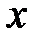, , 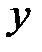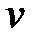в общем случае могут быть комплексными величинами.

3. В (8.1)–(8.3) величины 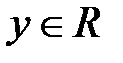, 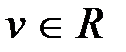могут быть скалярными, т.е. уравнения (8.1)–(8.3) могут описывать как многомерные, так и одномерные системы.

4. Уравнениями (8.1)–(8.3) могут быть описаны любые динамические системы: отдельные элементы и устройства, объект управления, регулятор, вся САУ в целом.

27. Последовательные корректирующие устройства.

Последовательные корректирующие устройства включаются в прямую цепь системы управления в соответствии с рис. 9.1, а.

При последовательной коррекции передаточная функция разомкнутой скорректированной системы будет равна 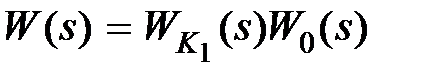. Выбором передаточной функции 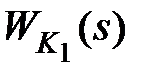можно добиться требуемой передаточной функции W(s), обеспечивающей желаемые свойства системы.

Последовательная коррекция часто применяется для обеспечения заданной точности системы. В этом случае передаточная функция корректирующего устройства выбирается в виде 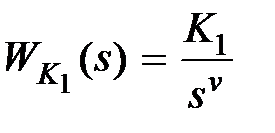, т.е. в прямую цепь системы вводится усилительное звено с коэффициентом усиления 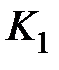и интегрирующее звено с передаточной функцией 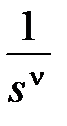, так что 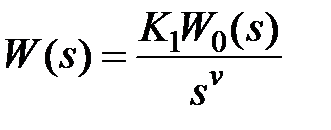. Выбор величин 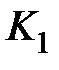и 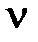обусловлен необходимой точностью системы в установившихся режимах. пусть исходная система статическая, 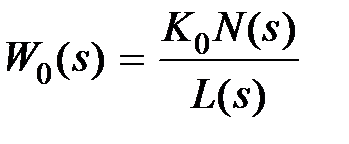и требуется, чтобы она имела статическую ошибку 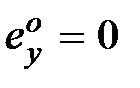и скоростную ошибку 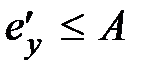. В соответствии с результатами подразд. 6.1 требуется, чтобы скорректированная система обладала астатизмом первого порядка, а общий коэффициент усиления 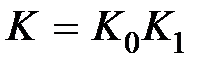был выбран из условия 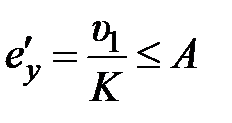, откуда 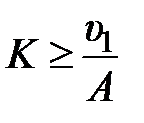, где величина 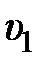задана. Таким образом, параметры корректирующего устройства 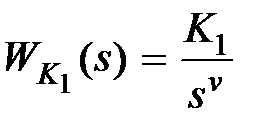следует выбрать из условия , .

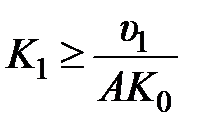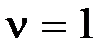В случае задания точности системы при отработке гармонического сигнала требуемый общий коэффициент усиления 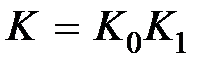(и соответственно величина 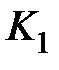) и порядок астатизма можно найти аналогично, если воспользоваться выражениями (6.17), (6.19).

Наряду с использованием последовательных корректирующих устройств для повышения точности эти устройства могут использоваться и для улучшения показателей качества системы. В этом случае в соответствии с выражением (9.1) выбором 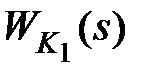изменяют среднечастотную часть исходной частотной характеристики 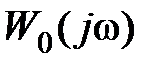, добиваясь требуемой частотной характеристики .

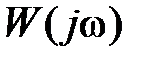Последовательные корректирующие устройства в виде пассивных или активных четырехполюсников обычно включаются после устройства сравнения или между каскадами предварительного усилителя. При этом применяют устройства с отставанием по фазе, с опережением по фазе и с отставанием и опережением по фазе.

На рис. 9.2, а представлены частотные характеристики системы при коррекции с отставанием по фазе. Здесь 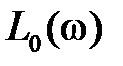– ЛАХ исходной системы, 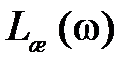– ЛАХ желаемой (скорректированной) системы, 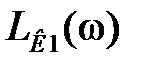– ЛАХ корректирующего устройства. На рис. 9.2, б изображена цепочка, реализующая эту коррекцию.

Рис. 9.2

Комплексная передаточная функция корректирующего устройства равна

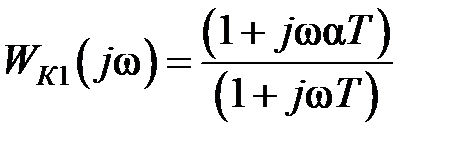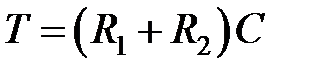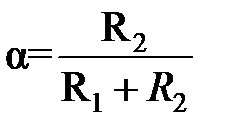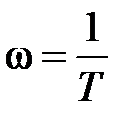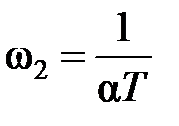, , , , . (9.4)

Эта коррекция приводит к повышению устойчивости, подавлению высокочастотных помех, но к снижению быстродействия.

На рис. 9.3 изображены частотные характеристики и цепочка при коррекции с опережением по фазе. Надо помнить, что цепочка вносит ослабление 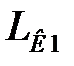, которое необходимо скомпенсировать.

Рис. 9.3

Комплексная передаточная функция корректирующего устройства:

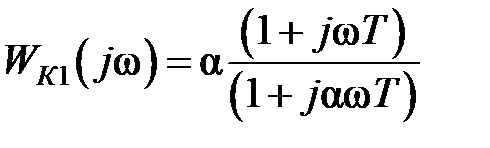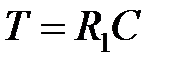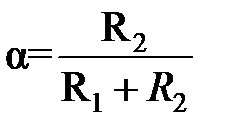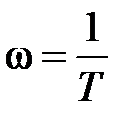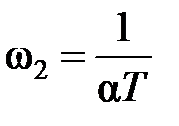, , , , . (9.5)

Эта коррекция приводит к повышению устойчивости и быстродействия, но к снижению помехоустойчивости на высоких частотах.

Объединение этих двух видов коррекции позволяет расширить среднечастотную зону (рис. 9.4).

В этом случае

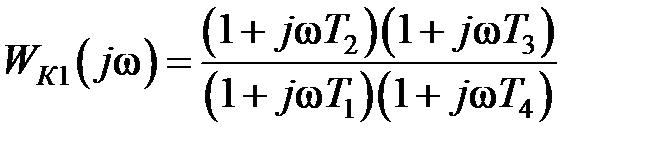, (9.6)

где , , ,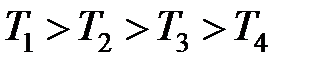

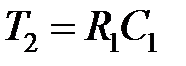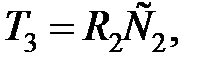
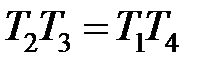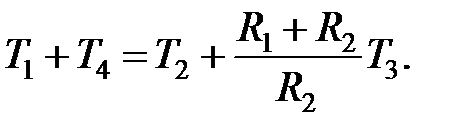
Рис. 9.4

Эта коррекция существенно улучшает качественные показатели САУ.

28. Параллельные корректирующие устройства.

Одним из распространенных способов улучшения качества системы является введение производной от сигнала в прямой цепи. Пусть на рис. 9.1, б 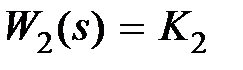, , 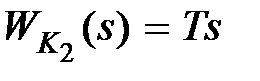тогда передаточная функция прямой цепи скорректированной системы будет равна 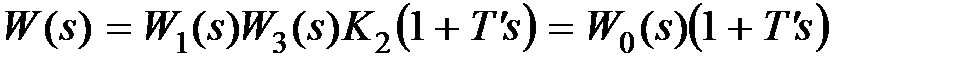, где .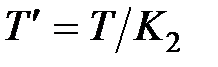

Введение корректирующего устройства изменяет амплитудную и фазовую характеристики системы, которые примут вид

, ,

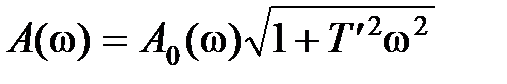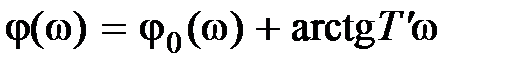(9.7)

, .

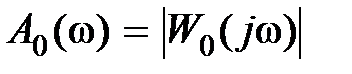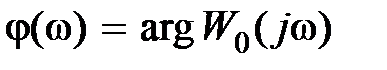Из (9.7) следует, что введение производной увеличивает положительные фазовые сдвиги и позволяет при соответствующем выборе 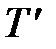в области частоты среза системы «поднять» фазовую характеристику и увеличить запасы устойчивости. При этом при малых частотах вид частотных характеристик исходной и скорректированной системы не изменится. Такая коррекция часто применяется для стабилизации или демпфирования систем.

Так как реализовать звено, осуществляющее чистое дифференцирование 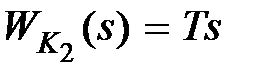, достаточно сложно, то используют введение производной с инерционностью, что соответствует 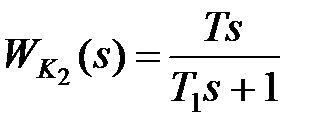. При этом эффект демпфирования несколько ослабевает.

Другой вид параллельного корректирующего устройства, находящего широкое применение, – это введение интеграла и производной от сигнала прямой цепи. Пусть 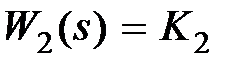, a 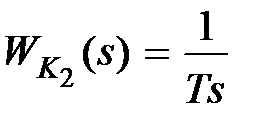, тогда передаточная функция прямой цепи будет равна 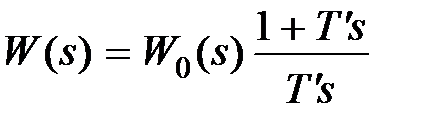, а ее частотные характеристики

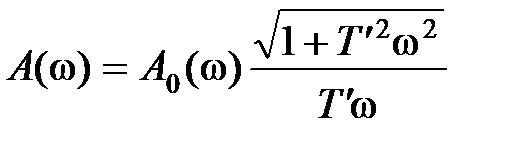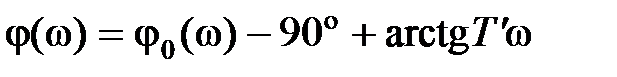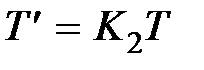, , . (9.8)

В системе повышается порядок астатизма на единицу и соответственно увеличивается точность. При этом путем выбора величины 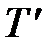, как следует из (9.8), отрицательный фазовый сдвиг в значительной степени можно на частоте среза скомпенсировать положительным 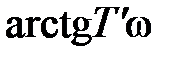, что позволяет обеспечить устойчивость системы.

29. Встречно-параллельные корректирующие устройства.

Встречно-параллельные корректирующие устройства выполняются в виде местных обратных связей. Наиболее часто обратными связями охватывают силовую часть системы управления (исполнительные элементы и усилители мощности).

Рассмотрим общие свойства таких корректирующих устройств. Для рис. 9.1, в частотная характеристика участка, охватываемого обратной связью, имеет вид .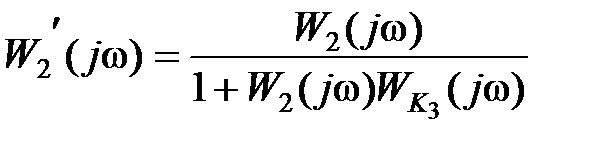

Обычно в диапазоне рабочих частот системы (в диапазоне низких частот) выполняется условие 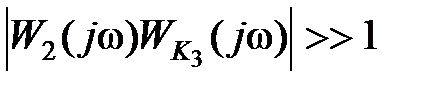и частотная характеристика 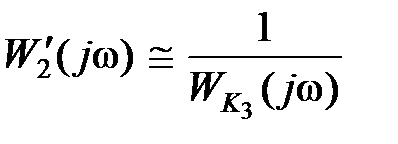, т.е. характеристика участка цепи, охваченного обратной связью, определяется только видом частотной характеристики корректирующего элемента и не зависит от звена прямой цепи 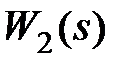. В ряде случаев это позволяет скомпенсировать нежелательное влияние звена 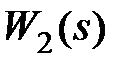на динамику системы, например, влияние малых нелинейностей или малого изменения параметров этого звена прямой цепи.

В зависимости от вида передаточной функции 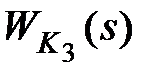корректирующие обратные связи делятся на жесткие и гибкие. Если звено 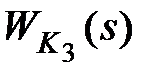является статическим ( 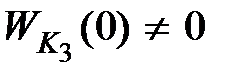), то обратная связь называется жесткой. Если звено 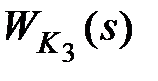является звеном дифференцирующего типа ( 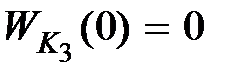), то имеем гибкую обратную связь. Жесткая обратная связь действует как в переходных, так и в установившихся режимах, а гибкая – только в переходных.

Рассмотрим несколько частных задач коррекции с помощью обратных связей.

Пусть 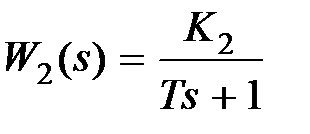, 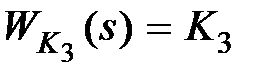. Тогда передаточная функция участка цепи 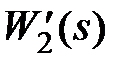, охваченного отрицательной обратной связью, будет иметь вид

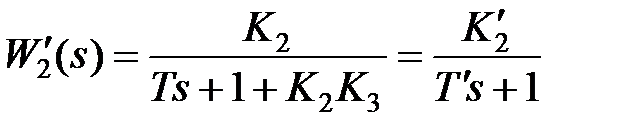, где , .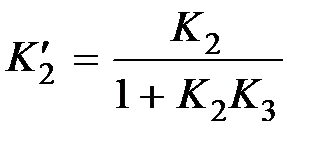

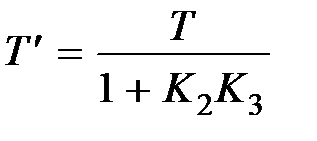Итак, структура звена не изменилась, оно осталось апериодическим, но произошло уменьшение коэффициента передачи и эквивалентной постоянной времени 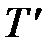. Отсюда следует, что охват в прямой цепи наиболее инерционного звена позволяет уменьшить инерционность всей цепи, что благоприятно сказывается на показателях качества системы (быстродействии, устойчивости). Уменьшение коэффициента передачи можно компенсировать введением дополнительного усилительного устройства.

Пусть 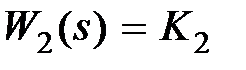, , 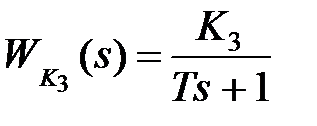тогда 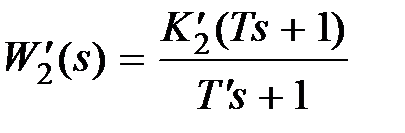, , 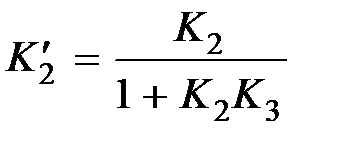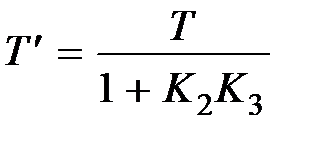. в этом случае меняется тип звена. При 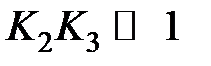, и можно записать приближенное выражение для передаточной функции 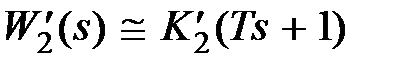. Итак, получили эквивалентное форсирующее звено, влияние которого аналогично влиянию введения производной при параллельной коррекции.

Рассмотрим изменение свойств охваченного участка прямой цепи при охвате его гибкой обратной связью. Пусть , .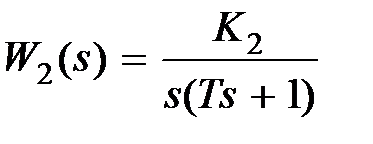

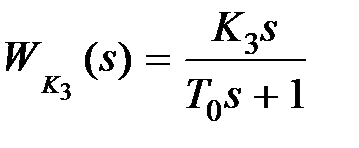В этом случае передаточная функция участка цепи с обратной связью 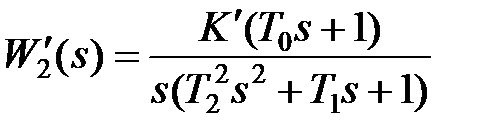, где , , .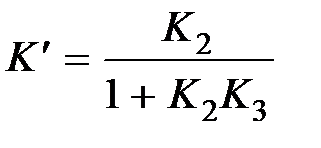

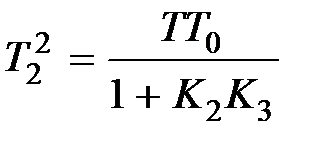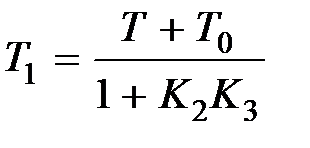Итак, при сохранении интегрирующих свойств эквивалентная передаточная функция обладает форсирующими свойствами из-за сомножителя 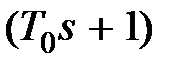. Если сделать величину 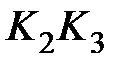достаточно большой, то малыми постоянными времени 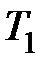и 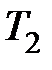можно пренебречь. При этом получим 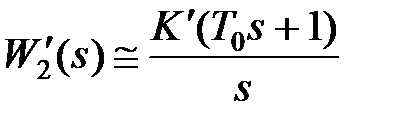, 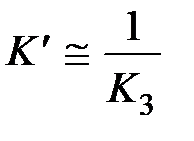. В этом случае получаем в прямой цепи изодромное звено.

30. Корректирующие устройства по внешнему воздействию.

При изменении передаточной функции прямой цепи с помощью последовательных, параллельных или встречно-параллельных корректирующих устройств для достижения заданных показателей качества неизменным остается главный принцип построения системы – принцип обратной связи (управление по отклонению). Учет внешнего воздействия при коррекции, в частности применение принципа компенсации (управление по возмущению) совместно с управлением по отклонению, позволяет расширить возможности коррекции системы.

Системы, использующие как управление по отклонению, так и по возмущению, относятся к классу комбинированных систем управления (см. подразд. 1.1). Наиболее часто комбинированное управление применяется для повышения точности системы управления и уменьшения установившейся ошибки. При определенных условиях с помощью комбинированного управления можно свести установившуюся ошибку к нулю при любой форме внешнего воздействия. Такое свойство называется инвариантностью системы по отношению к внешнему воздействию.

На рис. 9.5, а представлена структура комбинированной системы с корректирующим устройством по управляющему воздействию, а на рис. 9.5, б –
с корректирующим устройством по возмущению, где в первом случае передаточная функция корректирующего устройства обозначена через 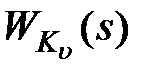, а во втором – через .

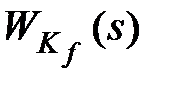Передаточная функция замкнутой системы без коррекции, связывающая выход y со входом 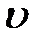, для обоих случаев имеет вид

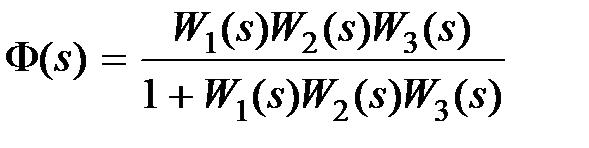. (9.9)

Найдем связь изображений выходного сигнала y с внешними
воздействиями.

Рис. 9.5

Для структуры, изображенной на рис. 9.5, а, имеем

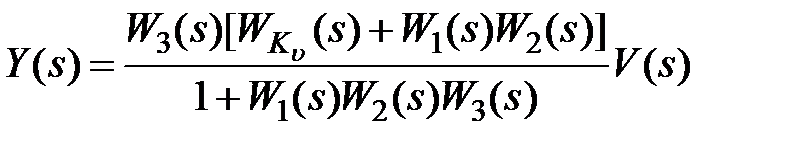, (9.10)

а для структуры на рис. 9.5, б имеем

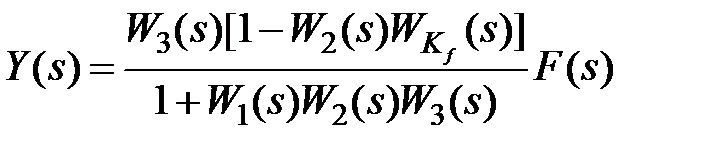. (9.11)

Задача любой системы автоматического управления – как можно более точно воспроизвести управляющий (полезный) сигнал 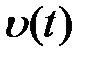и максимально ослабить влияние возмущения на выходной сигнал. С этой точки зрения желательно, чтобы в (9.10) передаточная функция, связывающая 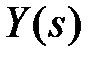и 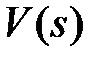, была равна единице (тогда 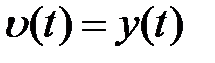), а передаточная функция в (9.11), связывающая 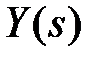и 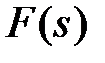, была равна нулю (тогда 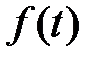не влияет на ).

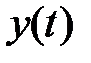Выполнением этих условий будут соответственно следующие соотношения:

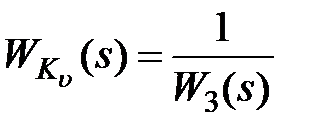, (9.12)

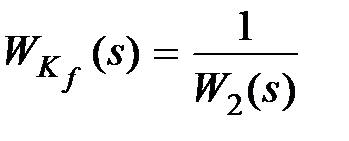. (9.13)

Условия (9.12), (9.13) соответствуют так называемой полной инвариантности системы. При выполнении (9.12) передаточная функция, связывающая ошибку е и входной сигнал 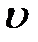, как это нетрудно проверить, будет равна нулю, т.е. ошибка в системе не зависит (инвариантна) от управляющего сигнала и всегда равна нулю. При выполнении (9.13) выход системы y не зависит (инвариантен) от возмущения f.

Отметим, что условия (9.12), (9.13) гарантируют инвариантность соответствующих координат с точностью до свободной составляющей, т.е. процессы, вызванные начальными отклонениями соответствующих координат и их производных, компенсироваться не будут.

Сравнивая (9.9)–(9.11), приходим к выводу, что характеристическое уравнение нескорректированной системы (9.9) и скорректированных систем (9.10), (9.11) одно и то же:

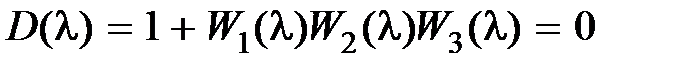, (9.14)

т.е. коррекция по внешнему воздействию не изменяет характеристического уравнения системы и соответственно свойств устойчивости (запасов устойчивости), а также ряда других показателей качества переходных процессов.

В силу этого контур управления по отклонению, как правило, используют для придания определенных динамических свойств системе, а контуры коррекции по внешним воздействиям – для обеспечения точности.

Точное выполнение условий инвариантности (9.12), (9.13) практически невозможно из условий физической реализуемости. Действительно, если в (9.12), (9.13) передаточные функции 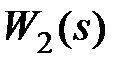, 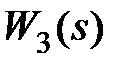соответствуют физически реализуемым звеньям, т.е. степени полиномов относительно 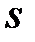их числителя меньше степеней знаменателя, то передаточные функци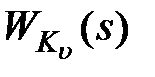и и 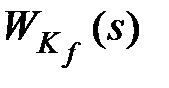, обратные им, будут соответствовать физически нереализуемым звеньям.

Поэтому (9.12), (9.13) выполняются на практике с некоторой погрешностью, в силу чего и инвариантность систем будет неполной, но ошибки в системе с помощью корректирующих устройств по внешнему воздействию могут быть значительно уменьшены.

31. Описание разомкнутых импульсных систем.

Структура разомкнутой импульсной системы приведена на рис. 1.4.

Рис. 1.4

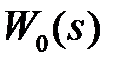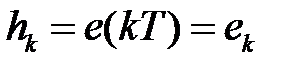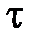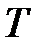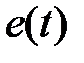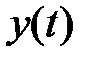Линейная непрерывная часть системы характеризуется передаточной функцией , а импульсный элемент законом модуляции и постоянными значениями величин и . Заметим, что сигналы и непрерывные, а 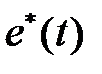- последовательность прямоугольных импульсов, модулированных по амплитуде.

Рассмотрим получение разностного уравнения на простейшем примере. Пусть 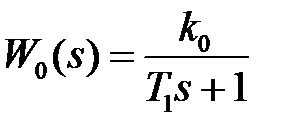, тогда 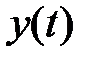и 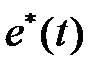связаны дифференциальным уравнением 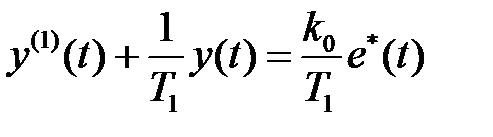, которое легко решается.

Обозначим значение координаты 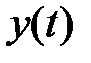в произвольный момент времени квантования 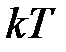через 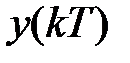, тогда на интервале действия 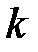-ого импульса 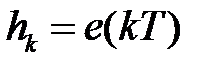и закон изменения выхода будет

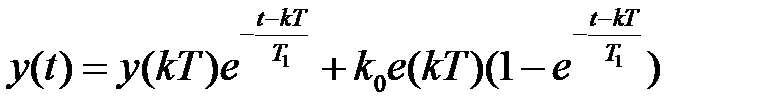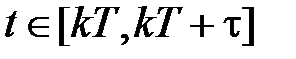, . (1.12)

Найдем закон изменения 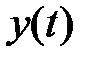на интервале паузы в 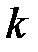-ом периоде, когда 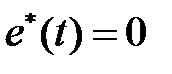. Он будет иметь вид

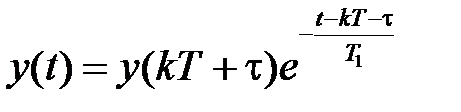. (1.13)

Полагая в (1.12) 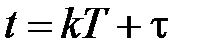, найдем 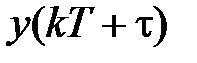, подставим в (1.13) и после преобразований будем иметь

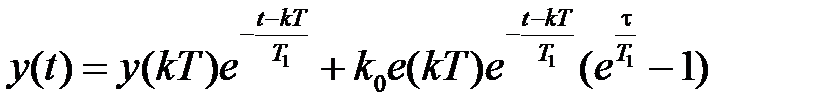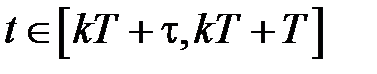, . (1.14)

Положим в (1.14) 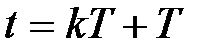и, обозначая 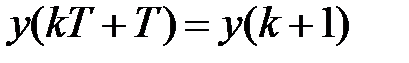, , 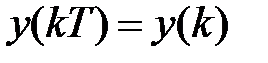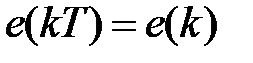будем иметь

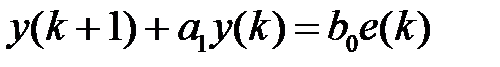, (1.15)

где , .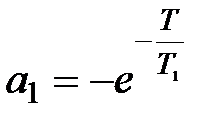

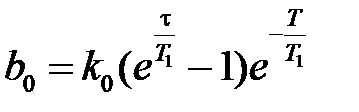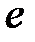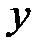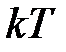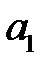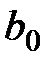Итак, связь и в дискретные моменты времени описывается линейным разностным уравнением первого порядка (частный случай (1.6)), коэффициенты которого и определены через параметры ИЭ и ЛНЧ.

Аналогично, можно получить разностное уравнение при 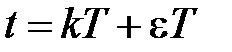, т.е. для смещенных решетчатых функций .

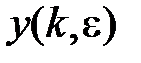Применяя к (1.15) 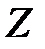-преобразование, найдем для данного случая передаточную функцию

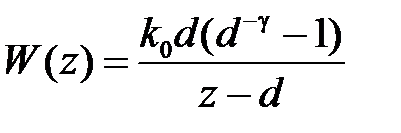
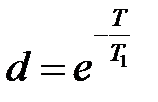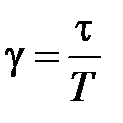, . (1.16)

Для простейших случаев передаточных функций 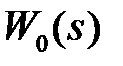можно по этой методике получить дискретные передаточные функции разомкнутой системы. Ниже приведем таблицу для трех вариантов передаточной функции .

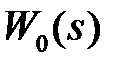Таблица 1.2

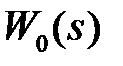
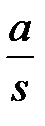
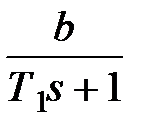
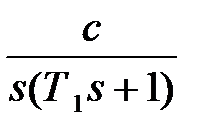
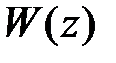
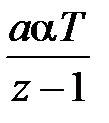
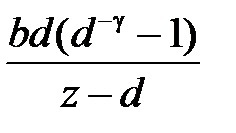
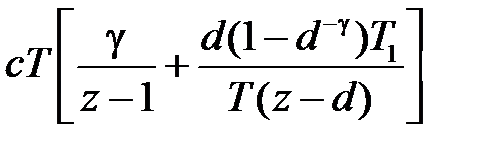
Если передаточная функция 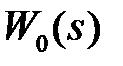имеет более высокий порядок, но может быть представлена в виде суммы передаточных функций 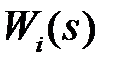простейшего типа , то в этом случае находя по табл. 1.2 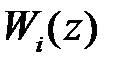, можно получить общую передаточную функцию разомкнутой системы

.

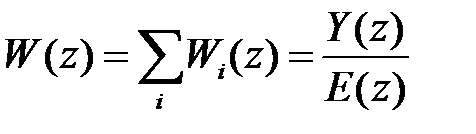Рассмотрим другой способ получения передаточной функции разомкнутой системы, излагаемый практически в любом учебнике. Структура на рис. 1.4 может быть представлена в виде, изображенном на рис. 1.5, а.

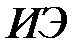
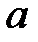
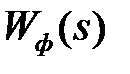
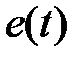
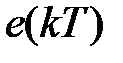
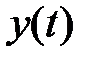
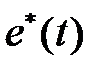
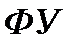
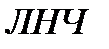
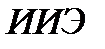
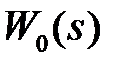
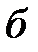
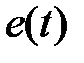
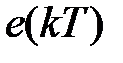
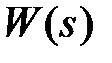
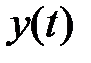
Рис.1.5

На рис. 1.5, а импульсный элемент представлен в виде идеального элемента (ИИЭ) или ключа и формирующего устройства (ФУ). Ключ периодически замыкается с периодом 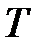и формирует последовательность импульсов в виде 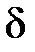-функций, площадь которых равна 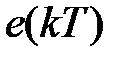. ФУ формирует последовательность прямоугольных импульсов 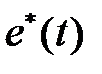, амплитуда которых равна .

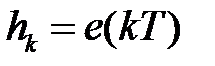По определению 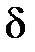- функция описывается так:

.

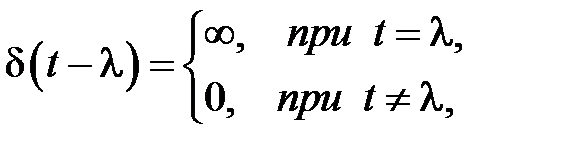
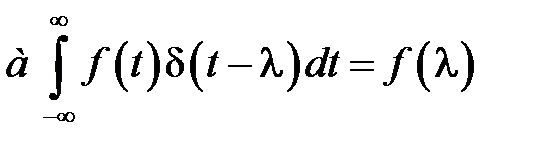Разумеется, физически ИИЭ не существует, однако такое математическое представление ИЭ отражает физику процессов в исходной структуре рис.1.3. Объединяя передаточные функци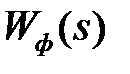и и 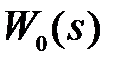, приходим к структуре рис.1.5, б, где ЭЛНЧ – эквивалентная линейная непрерывная часть с передаточной функцией 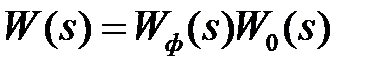. В случае прямоугольных импульсов 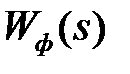имеет вид

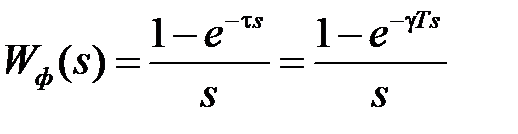, (1.17)

где .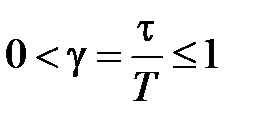

Если 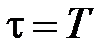, , 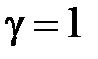то такое формирующее устройство называют фиксатором или экстраполятором нулевого порядка .

Если рассматривать 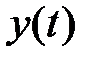для 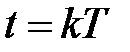, т.е. 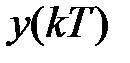и ввести изображения решетчатых функций 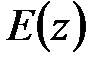, , 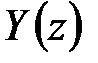то связь входа и выхода в области изображений будет 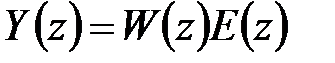, где передаточную функцию дискретной разомкнутой системы можно определить по выражению [6]

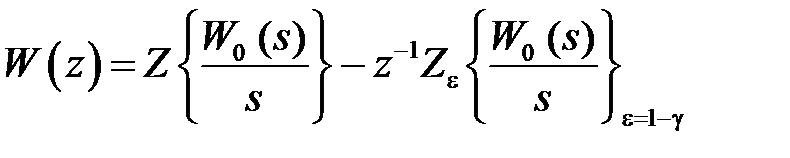. (1.18)

Отметим, что Z–преобразование применяется к решетчатым функциям. Однако каждой решетчатой функции 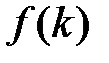соответствует непрерывная 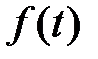, а ей некоторое изображение 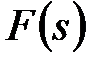. Поэтому 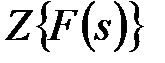будем понимать как символичную запись .

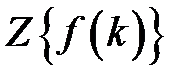Алгоритм применения формулы (1.18) следующий. Если 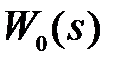имеет высокий порядок, то 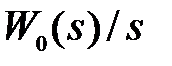представляют в виде суммы простейших (табличных) слагаемых. Далее по таблицам 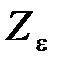–преобразования находят изображения каждого слагаемого и суммируют их. В результате получают изображение 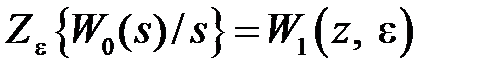. Полагая в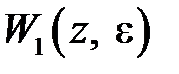 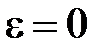, получают первое слагаемое в (1.18) и, полагая 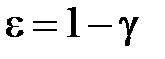, – второе.

Наиболее часто используется случай фиксатора нулевого порядка ( 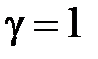). В этом случае формула (1.18) упрощается и имеет вид

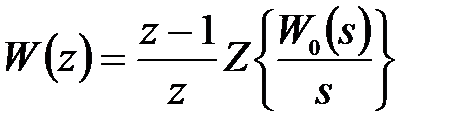. (1.19)

В наиболее общем случае передаточная функция 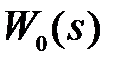может быть записана в виде 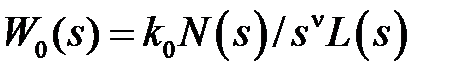. При этом всегда степень полинома 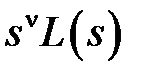больше степени полином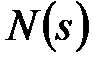а , а 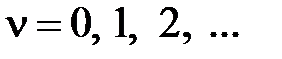характеризует порядок астатизма. В этом случае передаточная функция импульсной системы будет иметь вид

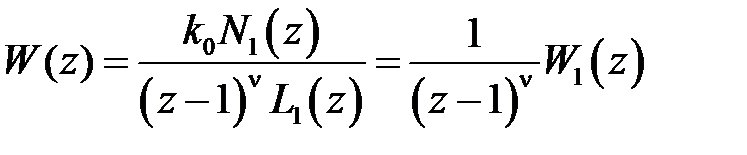, (1.20)

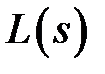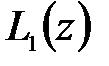причем степени полиномов и будут равны.

Для импульсной системы понятие порядка астатизма сохраняется, т.е. передаточная функция (1.20) соответствует импульсной системе с астатизмом 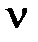-го порядка.

32. Частотные характеристики импульсных систем.

При описании и исследовании импульсных систем наряду с передаточными функциями и разностными уравнениями широкое распространение получили методы на базе частотных характеристик.

Если в формуле (1.7), определяющей прямое Z–преобразование, сделать замену переменной 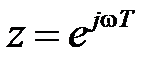, то получим соотношение

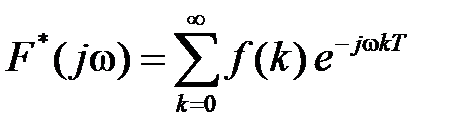, (1.23)

которое определяет прямое дискретное преобразование Фурье.

Пусть известна передаточная функция разомкнутой системы 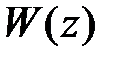, тогда после формальной замены 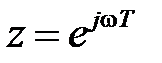получим 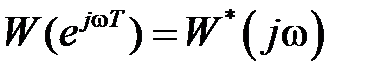, где 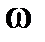– угловая частота.

Функция 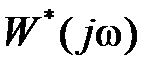называется амплитудно-фазовой частотной характеристикой (АФЧХ) импульсной системы. Далее знак будет относиться к частотным характеристикам импульсных систем. Характеристики без этого знака (например, 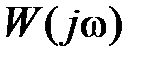) будут относиться к непрерывным системам.

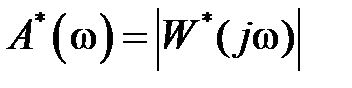называется амплитудной частотной характеристикой (АЧХ) системы, а 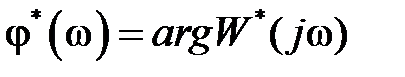– фазовой частотной характеристикой системы. Можно также ввести понятия вещественной и мнимой частотных характеристик.

Физический смысл частотных характеристик импульсной системы точно такой же, как и для непрерывной. Если на вход разомкнутой системы рис. 1.3 поступает гармонический сигнал 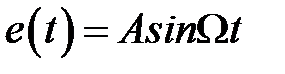, которому соответствует решетчатая функция 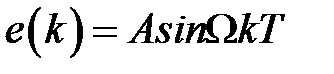, то на выходе в установившемся режиме будем иметь сигнал

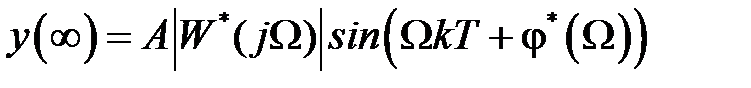, (1.24)

где 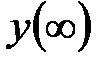здесь и далее будет обозначать установившееся значение сигнала или процесса при 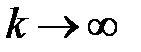или больших значений времени .

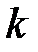Таким образом, АЧХ показывает, как изменяется амплитуда гармоники, а ФЧХ определяет величину фазового сдвига при прохождении гармоники через импульсную систему.

Так как 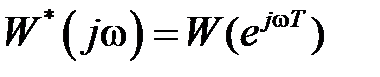, а 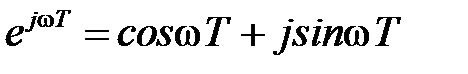, то в силу периодичности функци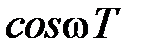й и 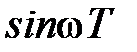частотные характеристики по отношению 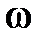являются периодическими функциями периода 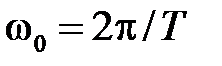, где здесь и далее 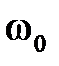– частота квантования (дискретизации) импульсного элемента.

Так же как для непрерывных систем и для импульсных САУ строятся график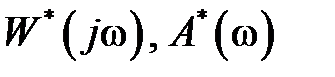и и 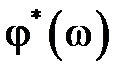на плоскости при изменении частоты 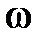. График 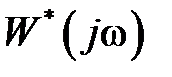является годографом на комплексной плоскости. Так как частотные характеристики периодические с периодом 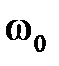, то их достаточно строить только на интервале частот от 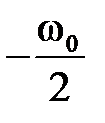до 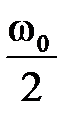. Более того 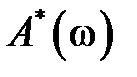– четная, а 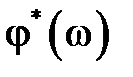нечетная функции своего аргумента, а годограф 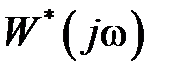симметричен относительно действительной оси. Поэтому характеристики обычно строятся на интервале частот от 0 до .

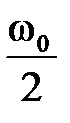Периодичность частотных характеристик отличает их от характеристик непрерывных систем, что является неудобным для получения логарифмических характеристик. Поэтому введем еще один класс частотных характеристик. В передаточной функции 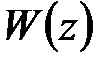сделаем замену комплексной переменной 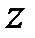на новую комплексную переменную 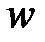по формулам:

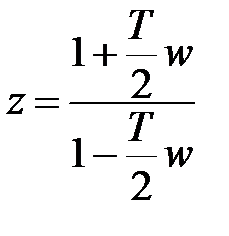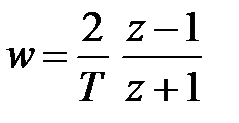, . (1.25)

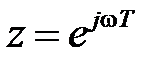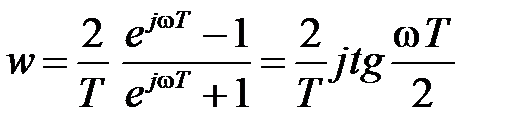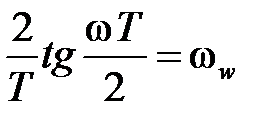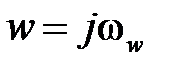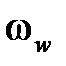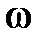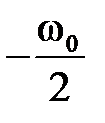Заменяя получим . Обозначим , тогда , где имеет размеренность угловой частоты и носит название псевдочастоты. При изменении от до 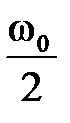псевдочастота изменяется от 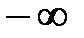до 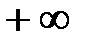. При малых 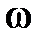частота 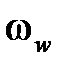близка к .

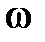Итак, заменяя 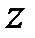на 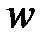, получим передаточную функцию 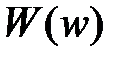, из которой, полагая 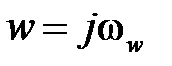получаем частотные характеристики 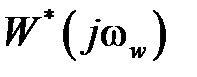, , 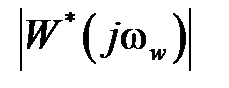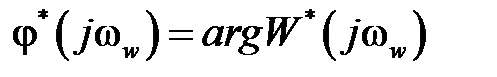– соответственно АФЧХ, АЧХ и ФЧХ относительно псевдочастоты.

Используя АЧХ и ФЧХ можно получить логарифмические характеристики 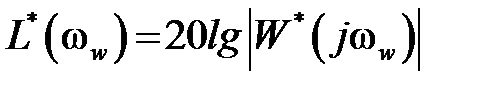– ЛАЧХ и 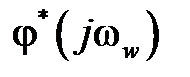– ЛФЧХ. Графики логарифмических характеристик строятся обычным образом, как и для непрерывных систем в логарифмическом масштабе.

В заключение рассмотрим одно из интересных свойств импульсных систем, связанное с периодичностью частотных характеристик. Пусть на вход разомкнутой системы поступает гармонический сигнал 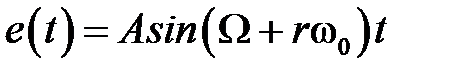, , 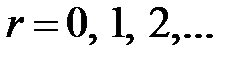которому соответствует решетчатая функция 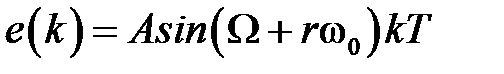. Тогда в соответствии с (1.24) в установившемся режиме на выходе будем иметь

.

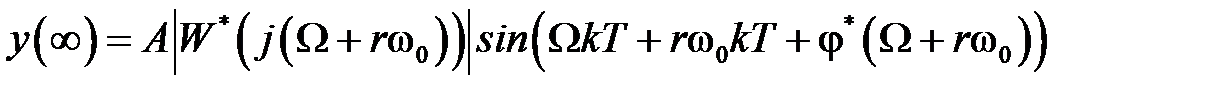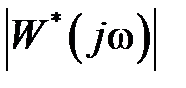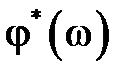В силу периодичности частотных характеристик и имеем 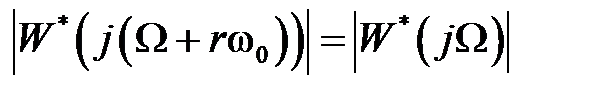, 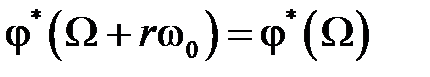. Кроме того с учетом 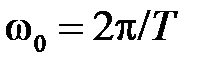можно записать 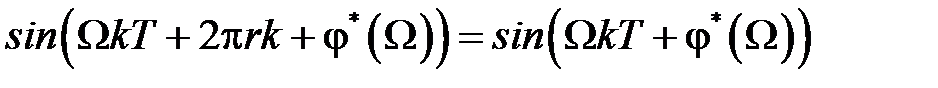. Окончательно получим 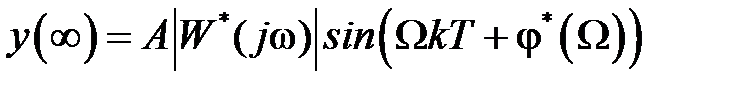, что совпадает с (1.24).

Итак, высокочастотная гармоника 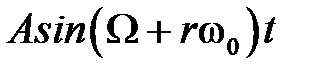и низкочастотная 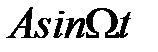на выходе разомкнутой импульсной системы дают один и тот же выходной сигнал. Это явление называется стробоскопическим эффектом, который заключается в переносе высокочастотных составляющих спектра входного сигнала в низкочастотную область.

33. Характеристики замкнутых импульсных систем.

Рассмотрим базовую структуру импульсной САУ (рис. 1.3). Пусть найдена передаточная функция разомкнутой импульсной САУ 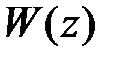, связывающая 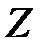-изображения выхода 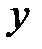и сигнала ошибки 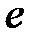. Тогда 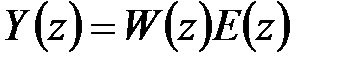. Очевидно, что 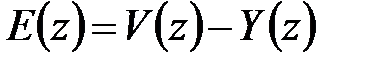. Из этих уравнений нетрудно получить два соотношения:

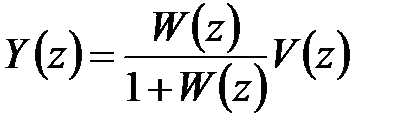, (1.33)

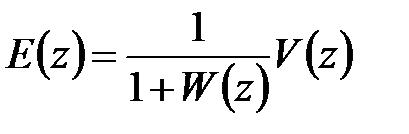. (1.34)

Введем следующие обозначения

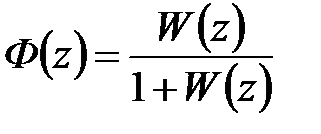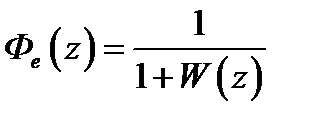, , (1.35)

тогда (1.33), (1.34) запишутся как , .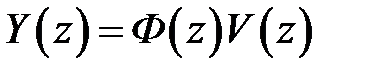

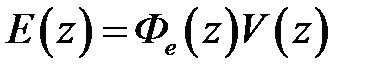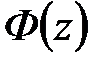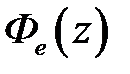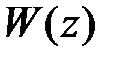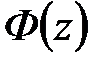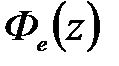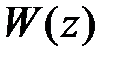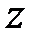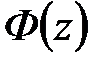Функцию будем называть главной передаточной функций замкнутой импульсной системы, а – передаточной функцией замкнутой импульсной системы по ошибке. Итак, зная , нетрудно найти и . Если есть отношение двух полиномов некоторых степеней относительно , то и 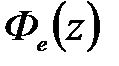также будут отношением полиномов. Поэтому в конечном итоге 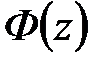можно представить в виде

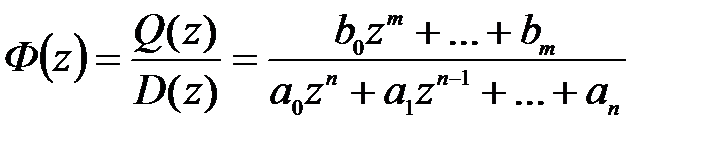. (1.36)

Используя (1.36) и связь 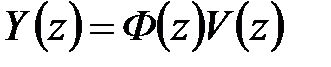, нетрудно найти разностное уравнение замкнутой импульсной системы, связывающее вход и выход

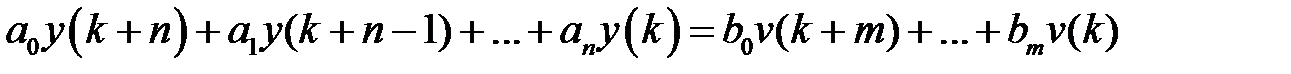. (1.37)

Кроме этого, введем еще одну важную характеристику системы – характеристическое уравнение замкнутой системы

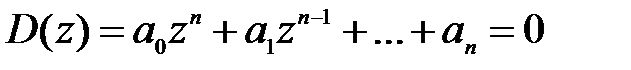, (1.38)

которое является алгебраическим уравнением n-ой степени. Полином 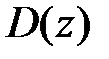называется характеристическим полиномом замкнутой системы.

Введем также понятие частотных характеристик замкнутой системы. Делая в передаточной функции 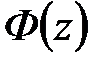замену 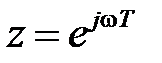получим частотные характеристики, из которых наиболее часто используются 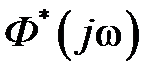– АФЧХ замкнутой системы, 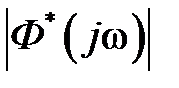– АЧХ замкнутой системы и 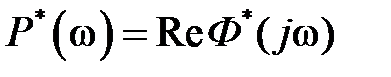– вещественная частотная характеристика замкнутой системы. Физический смысл этих частотных характеристик такой же, как и для разомкнутых систем.

Следующим классом характеристик импульсной системы являются временные характеристики: весовая функция импульсной системы 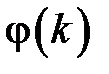и переходная функция импульсной системы 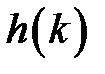, определяемые следующими соотношениями:

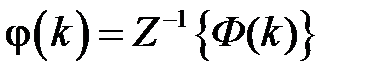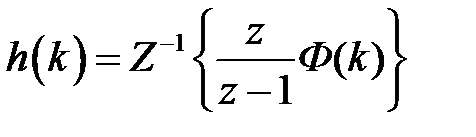, . (1.39)

Физический смысл временных характеристик следующий. Если на вход замкнутой системы поступает сигнал в виде ­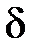функции 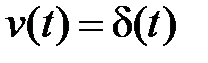, изображение которой 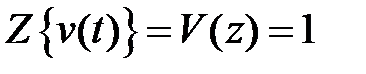, то изображение выхода будет равно 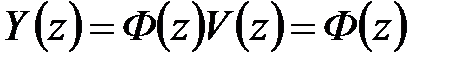. Таким образом, 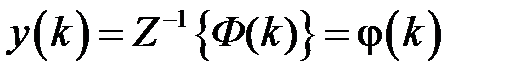, т.е. 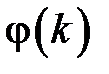есть реакция системы на сигнал в виде ­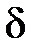функции. Если же на вход системы поступает сигнал в виде единичного ступенчатого воздействия 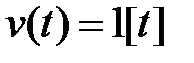, изображение которого равно 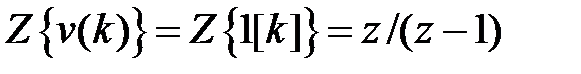, то изображение выхода будет 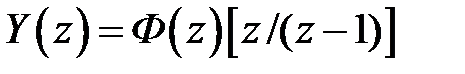, а оригинал 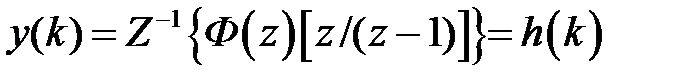. Таким образом, 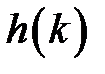– это реакция системы на единичное ступенчатое воздействие. Функци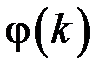и и 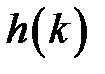связаны следующим соотношением .

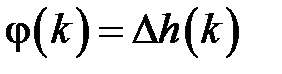Если для системы известна весовая функция 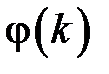, то при заданном входе 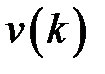выход определяется следующим образом:

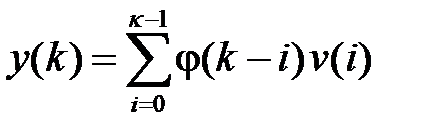. (1.40)

Выражение (1.40) представляет собой аналог интеграла свертки для импульсных систем.

34. Устойчивость процессов в импульсных системах.

Как отмечено в подразделе 1.5, замкнутая импульсная система характеризуется разностным уравнением (1.37) или передаточной функцией (1.36). Решение разностного уравнения всегда представимо в виде суммы свободной 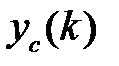и вынужденной 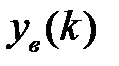составляющих (1.41). На устойчивость процессов, протекающих в импульсной системе, или на устойчивость импульсной системы, влияет только поведение свободной составляющей. Дадим определения устойчивости, аналогичные определениям для непрерывных систем .

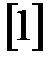Если с течением времени при 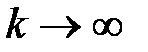свободная составляющая 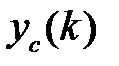затухает и стремится к нулю, т.е. 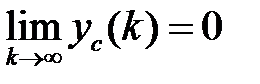, то система будет асимптотически устойчивой (далее просто устойчивой).

Есл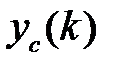и при 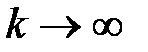неограниченно возрастает, т.е. 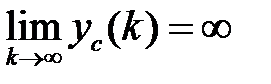, то система будет неустойчивой.

Наконец, если при 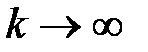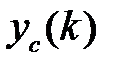не возрастает до бесконечности и не затухает до нуля, то система будет нейтральна или находится на границе устойчивости.

Устойчивость системы, как сейчас покажем, зависит от корней характеристического уравнения замкнутой системы

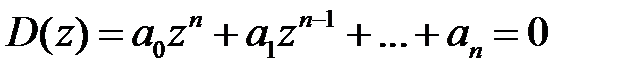. (1.44)

Если уравнение (1.44) имеет 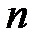простых (различных) корней 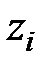, то свободная составляющая имеет следующий вид

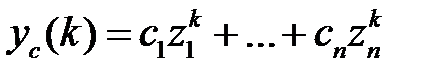, (1.45)

где 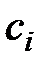- произвольные постоянные.

Из (1.45) нетрудно видеть, что если все 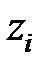– действительные величины и все модули 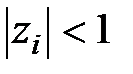, то при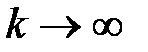 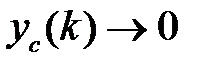, т.е. система устойчива. Если какой-либо корень 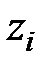комплексный, т.е. 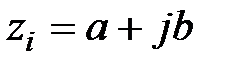, то его можно представить в виде 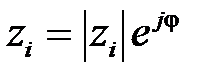, , 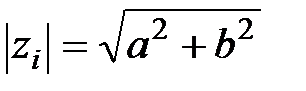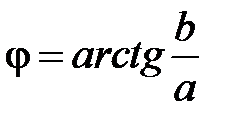. В силу этого составляющая 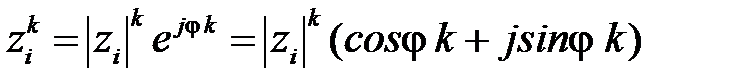и при 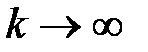эта составляющая будет стремиться к нулю.

Рассмотренное выше можно распространить на случай произвольных корней уравнения (1.44) и сформулировать следующее условие: необходимым и достаточным условием устойчивости импульсной системы является выполнение условия

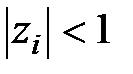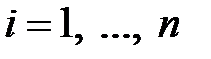, , (1.46)

т.е. модули всех корней характеристического уравнения (1.44) должны быть меньше единицы.

Если 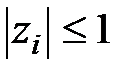, , 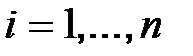то система нейтральна, а если существует хотя бы один корень, модуль которого больше единицы, то система неустойчива.

Для оценки устойчивости, нет необходимости находить корни уравнения (1.44). Разработаны специальные критерии устойчивости для импульсных систем, которые являются аналогами соответствующих критериев непрерывных систем. Существуют их две разновидности: алгебраические и частотные. Начнем рассмотрение с алгебраического критерия.

В уравнении (1.44) сделаем замену комплексной переменной 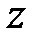на новую комплексную переменную 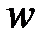по формуле

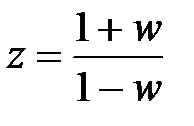. (1.47)

Замена (47) аналогична (25) , только множитель 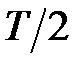при 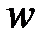опускается.

В результате замены от (1.44) придем к уравнению 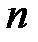-ой степени относительно .

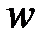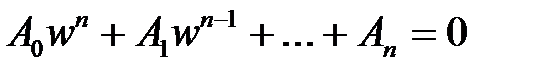, (1.48)

Формулы, связывающие 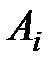с 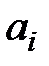приводятся в литературе [6].

Замена (1.47) обладает следующими свойствами:

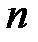- корням 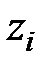уравнения (1.44) однозначно соответствуют 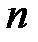корней 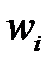уравнения (1.48) и наоборот;

- корню 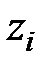уравнения (1.44), для которого 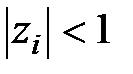, однозначно соответствует корень 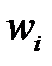уравнения (1.48), который будет иметь отрицательную действительную часть, т.е. .

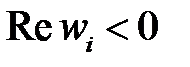На основании вышесказанного, если все корни 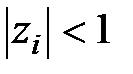, то все корни 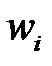будут с отрицательными действительными частями 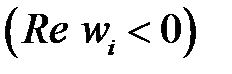и наоборот. Таким образом, для оценки устойчивости импульсной системы можно применить критерий Гурвица, разработанный для непрерывных систем.

Для уравнения (1.48) составим матрицу Гурвица [1]

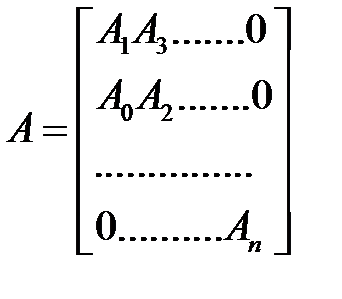(1.49)

и введем главные (диагональные) определители этой матрицы

, , .

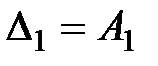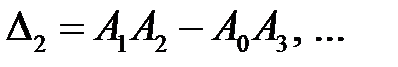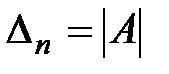Необходимым и достаточным условием устойчивости замкнутой импульсной системы будет выполнение неравенств

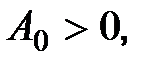
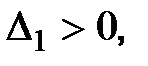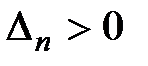…, . (1.50)

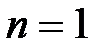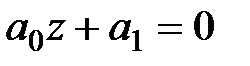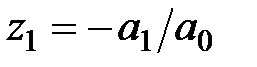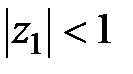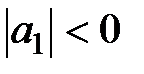Рассмотрим простейшие случаи. Пусть , тогда (1.44) будет: . Непосредственно находим корень уравнения . Условие устойчивости будет ,т.е. при .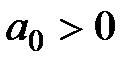

Пусть 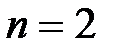, тогда (1.44) будет: 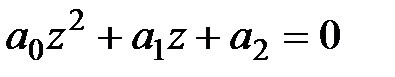. Замена (1.47) приведет к уравнению 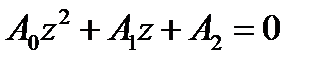, где 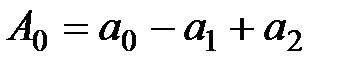, , 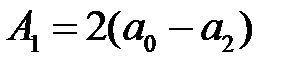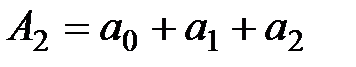. По критерию Гурвица получим условие устойчивости

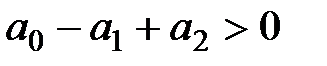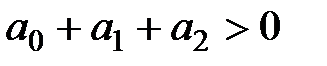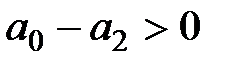, , . (1.51)

Для 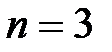условия устойчивости приведены в .

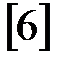Рассмотрим для импульсных систем частотный критерий устойчивости Найквиста, аналог критерия Найквиста для непрерывных систем. Для оценки устойчивости импульсной замкнутой системы базовой структуры (рис. 1.3) будем использовать АФЧХ разомкнутой системы 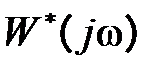. Формулировка критериев Найквиста для импульсных систем аналогична формулировке для непрерывных систем. Приведем одну из формулировок для случая, когда передаточная функция разомкнутой системы не имеет полюсов, модули которых больше единицы, т.е. разомкнутая система устойчива или нейтральна. Итак, критерий Найквиста: замкнутая система будет устойчива, если годограф 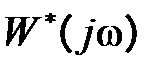при изменении 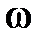от 0 до 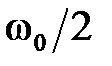не охватывает на комплексной плоскости точку с координатами .

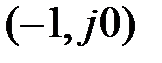Исследовать устойчивость также можно по логарифмическим характеристикам разомкнутой системы 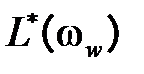и 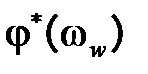. Формулировка вышеприведенного критерия Найквиста для логарифмических характеристик разомкнутой системы следующая: замкнутая импульсная система будет устойчивой, если до частоты среза 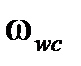фазовая характеристика 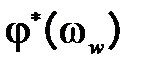не пересекает ось 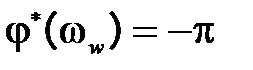, либо пересекает ее четное количество раз. Аналогично непрерывным системам вводятся понятия запасов устойчивости замкнутой импульсной системы по модулю 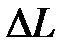и по фазе 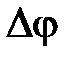. На рис. 1.7, например, показан случай устойчивой импульсной замкнутой системы и показаны запасы устойчивости , .

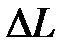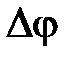При исследовании импульсных систем одной из важнейших задач является задача, связанная с определением областей устойчивости и выбором параметров из условий устойчивости. Коэффициенты 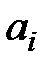характеристического уравнения (1.44) зависят от параметров импульсной системы: коэффициента усиления, постоянных времени, периода дискретизации и т.п. При одних значениях этих параметров система будет устойчивой, при других - неустойчивой.

Совокупность параметров, при которых система будет устойчивой, определяет область устойчивости в пространстве исследуемых параметров, а граница этой области будет границей устойчивости. Если число исследуемых параметров равно единице или двум, то области устойчивости можно интерпретировать как интервал (или интервалы) в случае одного параметра и как некоторые области на плоскости двух параметров во втором случае. При этом возможно графическое построение областей устойчивости.

Для определения областей устойчивости можно воспользоваться любыми критериями устойчивости. В случае небольшого порядка системы 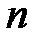удобно использовать критерий Гурвица для импульсных систем.

Пусть 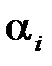, 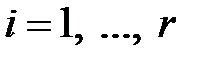-параметры системы, относительно которых определяется область устойчивости, тогда коэффициенты 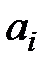характеристического уравнения (1.44) и соответственно коэффициенты 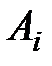уравнения (1.48) зависят от 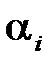. Таким образом, область устойчивости в пространстве параметров 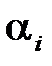будет определяться неравенствами (1.50), где 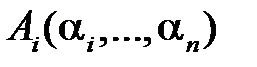, а границы этой области определяются уравнениями

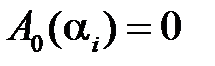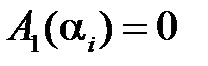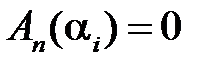, ,…, . (1.52)

35. Точность импульсных систем.

Точность замкнутой импульсной системы (рис. 1.3) в дискретные моменты времени 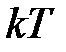определяется сигналом ошибки (рассогласования) 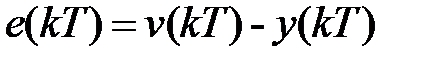, который характеризует текущую ошибку. Для оценки точности более удобно ввести, как это сделано для непрерывных систем, понятие установившейся ошибки 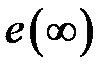, которая определяется для достаточно больших моментов времени 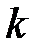после затухания переходной (свободной) составляющей процессов и в отличие от текущей ошибки часто является числом. Итак, при вычислении 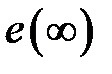будем полагать, что .

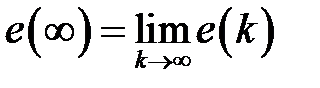Изображение сигнала ошибки и изображение входа связаны соотношением

,

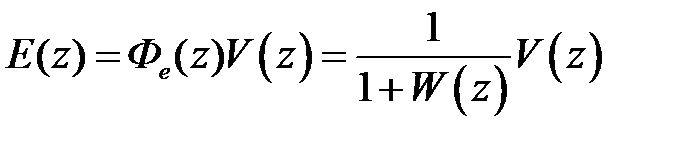где передаточную функцию разомкнутой системы будем брать в форме (1.22)

.

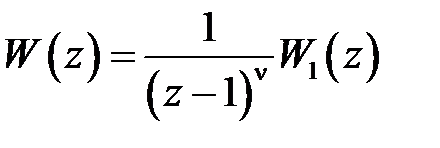Обычно оценивается точность импульсной системы на два вида воздействий: полиномиального и гармонического .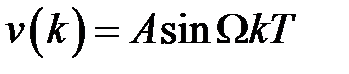

Частными случаями полиномиального воздействия являются единичная ступенчатая функция (скачок по положению) 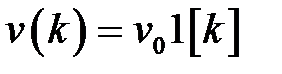, линейное воздействие (скачок по скорости) 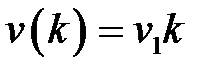и квадратичное воздействие (скачок по ускорению) .

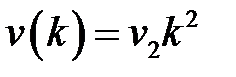В теории 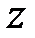-преобразования существует теорема о конечном значении решетчатой функции (оригинала)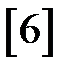

.

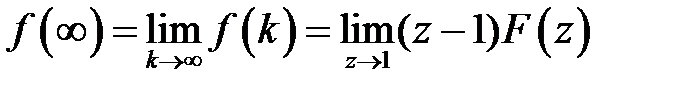Используя эту теорему, можно написать

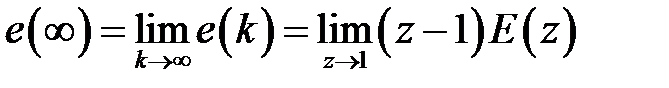, (1.57)

где .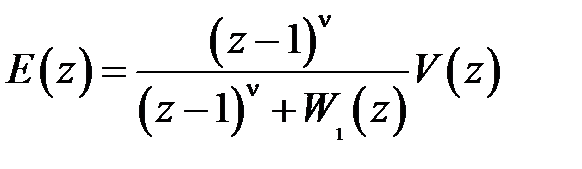

Рассмотрим частные случаи. Пусть 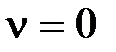, , 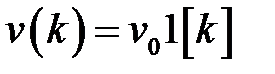тогда 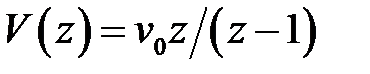и из (1.57) нетрудно получить 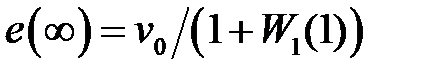. Т.к. 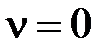соответствует статической системе, то такую ошибку называют статической.

Пусть 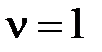, , 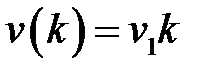тогда 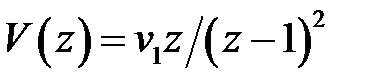и из (1.57) получим 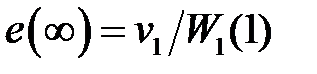. Такую ошибку будем называть скоростной. Нетрудно проверить, что в данном случае статическая ошибка будет равно нулю.

Пусть 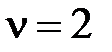, статическая и скоростная ошибки будут равны нулю, появится ошибка по ускорению. При этом все ошибки будут обратно пропорциональны величине .

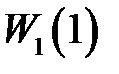Итак, можно сделать вывод, который является общим для импульсных систем: точность системы тем выше (ошибки тем меньше), чем выше порядок астатизма системы и больше величина 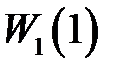. Так как 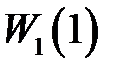прямо пропорциональна коэффициенту усиления 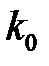линейной, непрерывной части системы 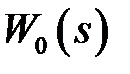, то увеличение 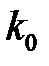будет приводить к повышению точности импульсной системы.

Точность системы в установившихся режимах также можно описывать по коэффициентам ошибок 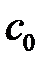, , 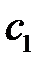…, которые имеют аналогичный непрерывным системам смысл и определяются по выражению :

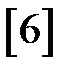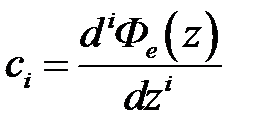½ 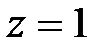, 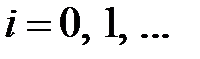. (1.58)

В частности для системы с астатизмом 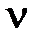-го порядка .

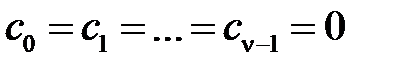Рассмотрим анализ точность системы при воспроизведении гармонического сигнала 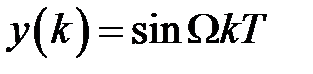, амплитуду которого будем полагать равной единице. Тогда в соответствии с (1.43) в установившемся режиме на выходе замкнутой системы сигнал будет иметь вид

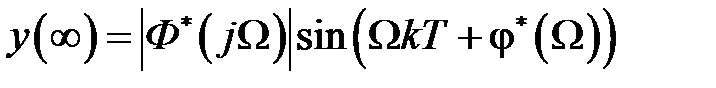, (1.59)

а ошибка в установившемся режиме будет

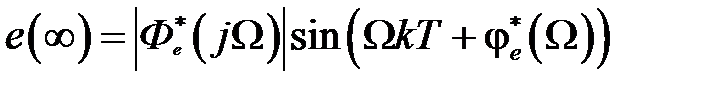, (1.60)

где 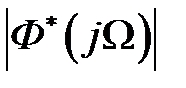, , 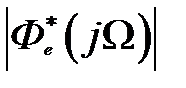, 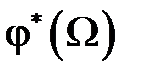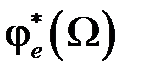- соответствующие значения модулей и сдвигов фаз, определенные по частотным характеристикам , .

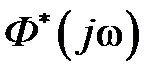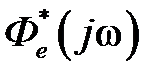Обычно в теории систем автоматического управления считают, что ошибки воспроизведения гармонического сигнала по фазе не имеют существенного влияния на работу САУ. Ошибки воспроизведения амплитуды из (1.59), (1.60) будут

,

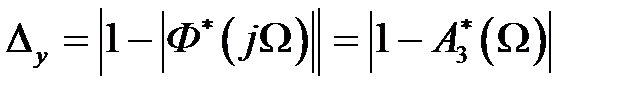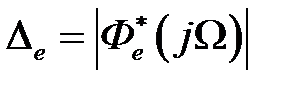. (1.61)

Обычно 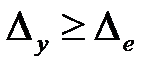, однако в диапазоне низких частот при малом можно считать .

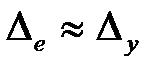Так же как и для непрерывных систем, для замкнутой импульсной системы можно ввести понятие полосы пропускания: это диапазон частот от 0 до 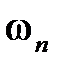, в котором ошибка воспроизведения гармонического сигнала 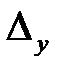не превышает заданной величины , т.е. .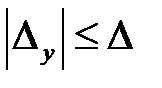

Так как 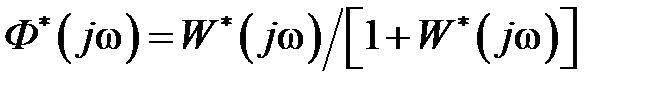, а 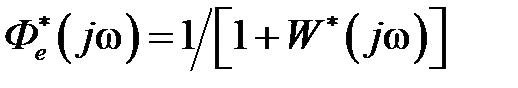, то для определения 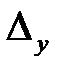и 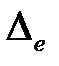в (1.61) можно использовать АФЧХ разомкнутой системы .

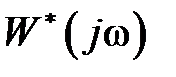Если частота входной гармоники достаточно низкая, то несложно показать, что при 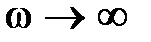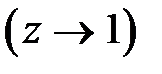для статических систем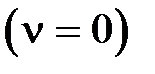 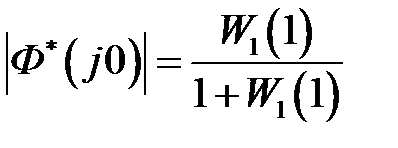, 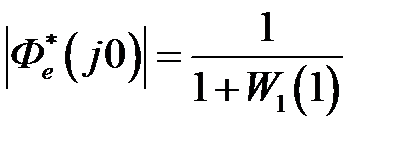и 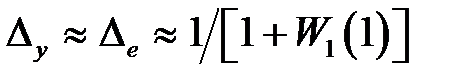. Для астатических систем 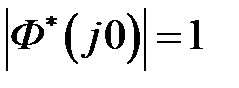, 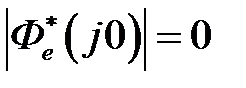и .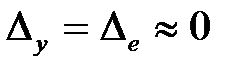

Таким образом, на точность воспроизведения гармонического сигнала влияет порядок астатизма и коэффициент усиления 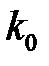непрерывной части системы, входящей в .

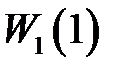В заключение отметим, что все изложенное имеет смысл только для устойчивых систем.