Для оценки склонности системы к колебаниям вводят так называемый показатель колебательности, который определяется как
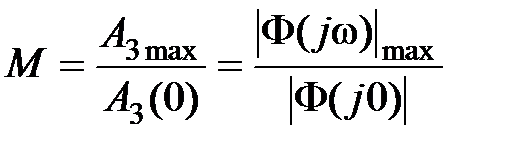 (7.21)
(7.21)
либо иногда как
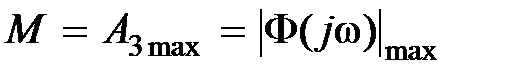 . (7.22)
. (7.22)
Так как 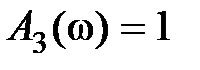 для астатических и
для астатических и 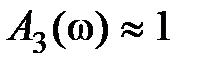 для статических систем при большом коэффициенте усиления K разомкнутой системы, то отличие выражений (7.21), (7.22) друг от друга незначительно.
для статических систем при большом коэффициенте усиления K разомкнутой системы, то отличие выражений (7.21), (7.22) друг от друга незначительно.
Физически показатель колебательности М характеризует склонность системы к колебаниям: чем больше М, тем более колебательный характер переходного процесса. Этот показатель имеет менее прозрачный смысл, чем,
например, время регулирования 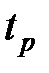 и перерегулирование
и перерегулирование  . Считается, что
. Считается, что
если М не превосходит величины 1,2–1,3, то качество процессов в системе будет удовлетворительным и при других внешних воздействиях, отличных от гармонических.
Величина М также косвенно характеризует запасы устойчивости системы: чем больше М, тем меньше запасы устойчивости. Однако количественно связать М и величины 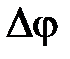 ,
, 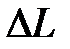 не удается.
не удается.
Для определения величины М можно воспользоваться графиком АЧХ разомкнутой системы 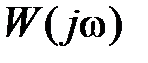 . Пусть
. Пусть 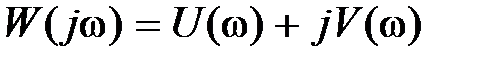 . Тогда
. Тогда 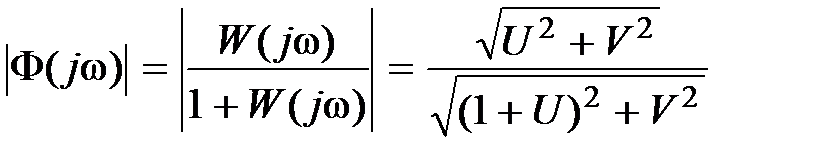 , откуда
, откуда 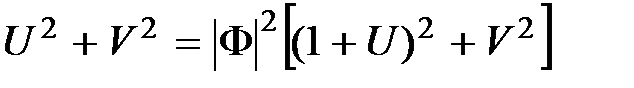 ,
,
или 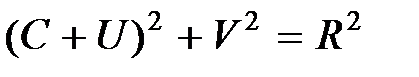 , (7.23)
, (7.23)
где 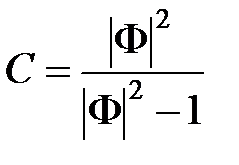 ,
, 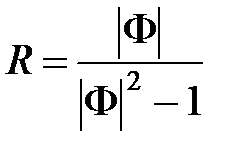 .
.
Задавая 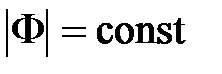 и находя С и R по уравнению (7.23) в комплексной плоскости u, jv, получим кривые, которые будут представлять собой окружности радиусом R с центрами на действительной оси. Эти окружности для разных значений
и находя С и R по уравнению (7.23) в комплексной плоскости u, jv, получим кривые, которые будут представлять собой окружности радиусом R с центрами на действительной оси. Эти окружности для разных значений 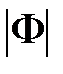 приведены на рис. 7.8.
приведены на рис. 7.8.
Рис. 7.8
Все эти окружности (линии равных значений 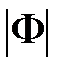 ) охватывают при
) охватывают при 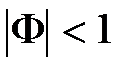 начало координат, а при
начало координат, а при 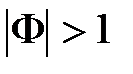 – точку с координатами (–1, j0). При
– точку с координатами (–1, j0). При 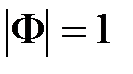 они вырождаются в прямую.
они вырождаются в прямую.
На рис. 7.8 нанесен график АЧХ 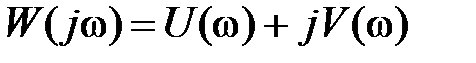 . Фактически представленная серия кривых при
. Фактически представленная серия кривых при 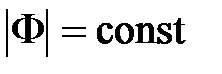 является номограммой для определения
является номограммой для определения 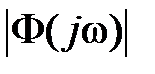 по кривой
по кривой 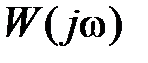 . В точках пересечения
. В точках пересечения 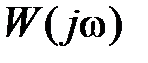 и соответствующей кривой
и соответствующей кривой 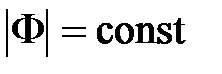 находим для заданного значения
находим для заданного значения 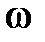 величину
величину 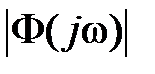 . Так, из рис. 7.8 видим, что при
. Так, из рис. 7.8 видим, что при 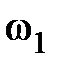 величина
величина 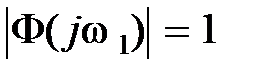 , при
, при 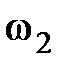 величина
величина 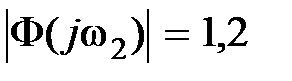 и т.д. Очевидно, что показатель колебательности М определится в точке касания годографа
и т.д. Очевидно, что показатель колебательности М определится в точке касания годографа 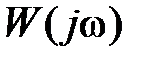 с окружностью, имеющей максимальное значение
с окружностью, имеющей максимальное значение 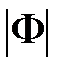 . Для данного случая видно, что это будет окружность, соответствующая M = 1,5.
. Для данного случая видно, что это будет окружность, соответствующая M = 1,5.
Из рис. 7.8 видно, что чем больше величина М (или 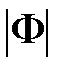 ) для данной системы, тем ближе АФЧХ
) для данной системы, тем ближе АФЧХ 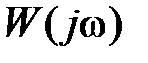 подходит к точке с координатами (–1, j0), тем меньше у системы будут запасы устойчивости.
подходит к точке с координатами (–1, j0), тем меньше у системы будут запасы устойчивости.
Наконец, возможна оценка качественных показателей системы по виду логарифмических частотных характеристик разомкнутой системы. Всю характеристику можно условно разбить по оси частот на три диапазона, как это показано на рис. 7.9, где НЧ – диапазон низких частот, СЧ – средних и ВЧ – высоких частот.
| | Логарифмическая характеристика 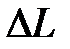 в диапазоне НЧ влияет на точностные характеристики системы, так как первая асимптота определяется двумя величинами: K – коэффициентом усиления разомкнутой системы и в диапазоне НЧ влияет на точностные характеристики системы, так как первая асимптота определяется двумя величинами: K – коэффициентом усиления разомкнутой системы и 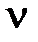 – порядком астатизма. Область средних частот вблизи частоты среза – порядком астатизма. Область средних частот вблизи частоты среза 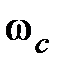 в значительной степени определяет такие показатели системы, как запасы устойчивости в значительной степени определяет такие показатели системы, как запасы устойчивости 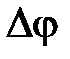 , , 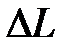 , время регулирования , время регулирования 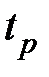 , ,
|
перерегулирование  , величину показателя колебательности М. Связать указанные параметры непосредственно с параметрами произвольной ЛАЧХ достаточно трудно. Однако для ряда частных случаев ЛАЧХ путем экспериментальных исследований получены графические зависимости, связывающие указанные величины. Отметим лишь одно общее свойство: чем больше величина
, величину показателя колебательности М. Связать указанные параметры непосредственно с параметрами произвольной ЛАЧХ достаточно трудно. Однако для ряда частных случаев ЛАЧХ путем экспериментальных исследований получены графические зависимости, связывающие указанные величины. Отметим лишь одно общее свойство: чем больше величина 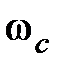 , тем меньше время регулирования. Кроме этого, считается, что для получения приемлемых показателей качества и обеспечения устойчивости желательно, чтобы наклон асимптоты на частоте среза
, тем меньше время регулирования. Кроме этого, считается, что для получения приемлемых показателей качества и обеспечения устойчивости желательно, чтобы наклон асимптоты на частоте среза 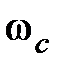 был –20 дБ/дек, а ее протяженность – не менее одной декады.
был –20 дБ/дек, а ее протяженность – не менее одной декады.
Область ВЧ существенного влияния на динамику системы не оказывает, поэтому при анализе ее обычно не учитывают.
26. Описание систем управления с помощью уравнений состояния.
Рассматриваемые в предыдущих разделах системы относятся к простейшему (классическому) типу САУ, характеризуемому одной регулируемой координатой (одномерные системы). Динамические процессы в них удобно описывать одним дифференциальным уравнением n-го порядка, передаточными функциями и частотными характеристиками. При описании многомерных или многосвязных систем, имеющих несколько регулируемых координат, такой подход встречает определенные трудности. Более естественной формой математического описания многомерных систем является векторно-матричная форма уравнений динамики или подход, базирующийся на применении уравнений состояния.
Преимуществом математических моделей в виде уравнений состояния является универсальность (применимость как для одномерных, так и для многомерных систем), компактность формы записи, а также более естественная форма записи для численных расчетов на ЭВМ. В силу этого с конца 60-х годов ХХ столетия в теории управления развиваются методы описания и исследования САУ на базе уравнений состояния.
При математическом описании любой системы всегда можно выделить три группы величин: 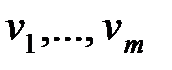 – входные сигналы, действующие на систему, включающие как управляющие, так и возмущающие сигналы;
– входные сигналы, действующие на систему, включающие как управляющие, так и возмущающие сигналы; 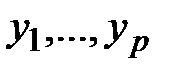 – выходные сигналы, несущие информацию о поведении системы, а также переменные
– выходные сигналы, несущие информацию о поведении системы, а также переменные 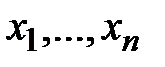 , характеризующие непосредственно саму систему (переменные состояния). физический смысл переменных
, характеризующие непосредственно саму систему (переменные состояния). физический смысл переменных 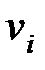 и
и 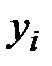 достаточно ясен. Переменные состояния
достаточно ясен. Переменные состояния 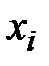 – это минимальный набор физических или абстрактных величин, который полностью определяет состояние системы в любой момент времени.
– это минимальный набор физических или абстрактных величин, который полностью определяет состояние системы в любой момент времени.
Объединим соответствующие группы переменных в векторы: 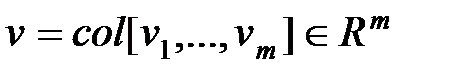 – вектор входа системы,
– вектор входа системы, 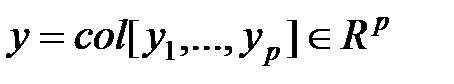 – вектор выхода системы (вектор наблюдения),
– вектор выхода системы (вектор наблюдения), 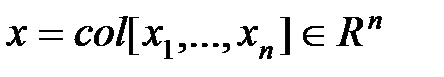 – вектор состояния,
– вектор состояния, 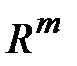 ,
, 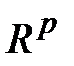 ,
, 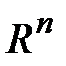 – евклидовы пространства соответствующих размерностей. Пространство
– евклидовы пространства соответствующих размерностей. Пространство 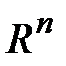 носит название пространства состояний.
носит название пространства состояний.
Так как нас интересует поведение системы во времени, т.е. динамика системы, то все соответствующие переменные и векторы будем полагать в дальнейшем функциями текущего времени t, т.е. 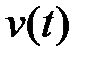 ,
, 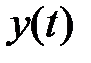 ,
, 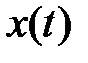 .
.
Под математической моделью системы будем понимать соотношения между векторами 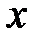 ,
, 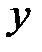 ,
, 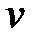 , описываемые при помощи математических операций и позволяющие однозначно определять закон изменения во времени
, описываемые при помощи математических операций и позволяющие однозначно определять закон изменения во времени
вектора выхода 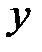 при заданном векторе входа
при заданном векторе входа 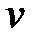 и начальном состоянии
и начальном состоянии
системы x.
В случае непрерывных систем наиболее общей формой математической модели являются уравнения вида

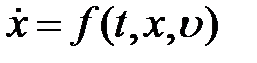 ,
, 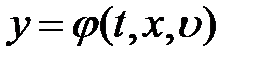 , (8.1)
, (8.1)
где 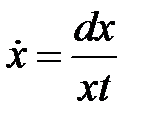 ,
, 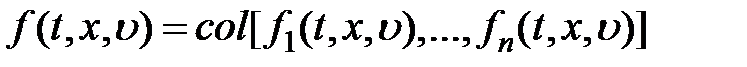 ,
, 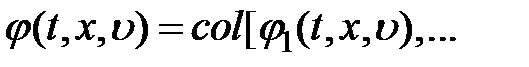
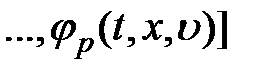 – вектор-функции соответствующих размерностей;
– вектор-функции соответствующих размерностей; 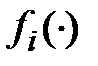 ,
, 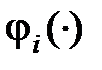 – скалярные функции.
– скалярные функции.








