Оценка носит название линейной интегральной оценки, – абсолютной интегральной и – квадратичной интегральной оценки.
Значение интегралов будет конечной величиной только в том случае, если 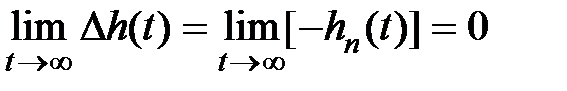 , т.е. только для асимптотически устойчивых систем.
, т.е. только для асимптотически устойчивых систем.
Поясним физический смысл оценок (7.8)–(7.10), для чего обратимся
к рис. 7.3. Для 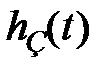 , соответствующих кривым 1, 2, 3 (см. рис. 4.2), построены графики отклонения
, соответствующих кривым 1, 2, 3 (см. рис. 4.2), построены графики отклонения 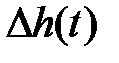 (на рис. 7.3 соответственно кривые 1, 2, 3).
(на рис. 7.3 соответственно кривые 1, 2, 3).
Величина 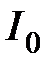 для кривой 1 есть величина площади, ограниченной этой кривой и координатными осями.
для кривой 1 есть величина площади, ограниченной этой кривой и координатными осями.
| | Очевидно, чем меньше 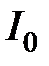 , тем меньше текущие отклонения , тем меньше текущие отклонения 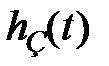 от установившегося значения и тем меньше будет время регулирования в системе. В идеальном случае, если от установившегося значения и тем меньше будет время регулирования в системе. В идеальном случае, если 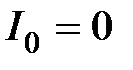 , время регулирования будет равно нулю. Для кривых 2, 3 в силу того, что они меняют свой знак, оценка , время регулирования будет равно нулю. Для кривых 2, 3 в силу того, что они меняют свой знак, оценка 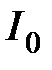 неприменима, так как величина интеграла может оказаться очень малой (даже равной нулю), но процессы будут затухать медленно. Поэтому линейные интегральные оценки можно применять, если неприменима, так как величина интеграла может оказаться очень малой (даже равной нулю), но процессы будут затухать медленно. Поэтому линейные интегральные оценки можно применять, если
|
заведомо известно, что переходная составляющая имеет монотонный характер.
Для колебательных процессов обычно применяются оценки 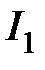 ,
, 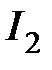 , которые имеют аналогичный смысл: чем меньше величина I, тем меньше время регулирования и меньше отклонения координаты системы от установившегося процесса.
, которые имеют аналогичный смысл: чем меньше величина I, тем меньше время регулирования и меньше отклонения координаты системы от установившегося процесса.
Любые интегральные оценки носят качественный и сравнительный характер, т.е. по величине I нельзя определить, например, время регулирования или перерегулирование в системе. Но если для двух вариантов проектируемой системы окажется, что 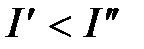 , то считается, что качественные показатели первой системы лучше, чем второй.
, то считается, что качественные показатели первой системы лучше, чем второй.
Наиболее просто вычисляются интегральные оценки 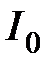 и
и 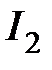 . Пусть передаточная функция замкнутой системы имеет вид
. Пусть передаточная функция замкнутой системы имеет вид
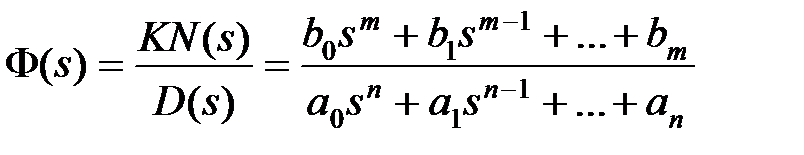 . (7.11)
. (7.11)
Найдем изображение отклонения 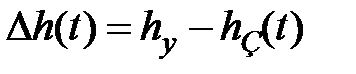 с учетом того, что
с учетом того, что 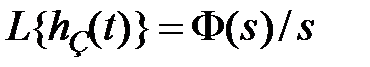 ,
, 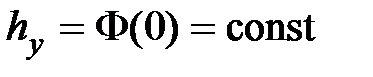 и
и 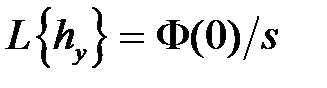 :
:
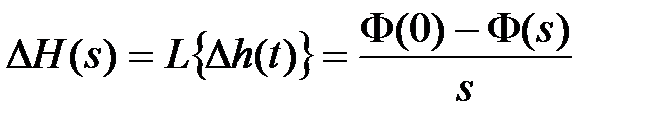 . (7.12)
. (7.12)
Так как 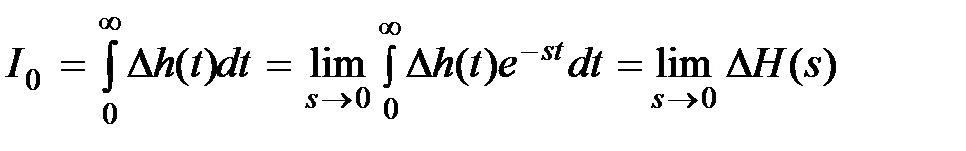 , то с учетом (7.11) имеем
, то с учетом (7.11) имеем
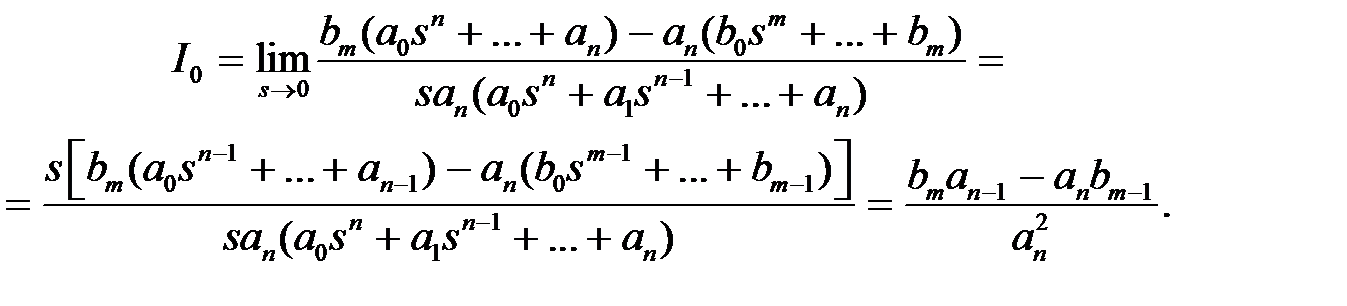
| (7.13) |
квадратичная интегральная оценка 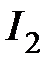 может быть определена на основе
может быть определена на основе
формулы Парсеваля (или Релея).
В частности, для астатических систем
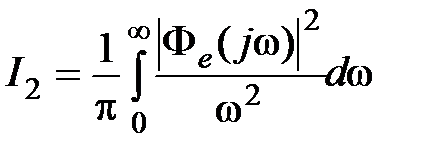 . (7.14)
. (7.14)
Изображение отклонения 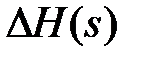 всегда можно представить как отношение двух полиномов:
всегда можно представить как отношение двух полиномов:
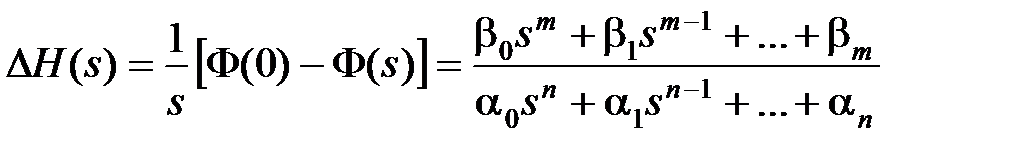 . (7.15)
. (7.15)
При этом оценка 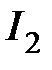 может быть аналитически вычислена при m < n через коэффициенты
может быть аналитически вычислена при m < n через коэффициенты 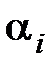 ,
, 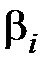 (7.15). Выражение для вычисления
(7.15). Выражение для вычисления 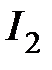 имеет достаточно сложный вид и здесь не приводится. Для наиболее распространенного случая
имеет достаточно сложный вид и здесь не приводится. Для наиболее распространенного случая
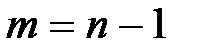 приведем несколько конечных выражений для вычисления
приведем несколько конечных выражений для вычисления 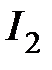 :
:
| (7.16) |
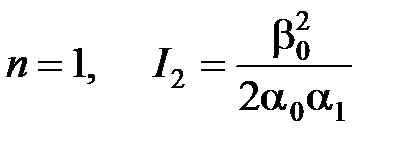 ;
; 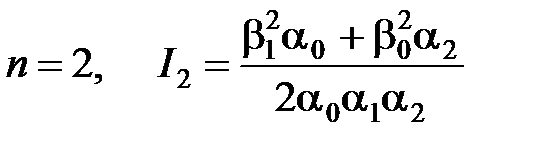 ;
;
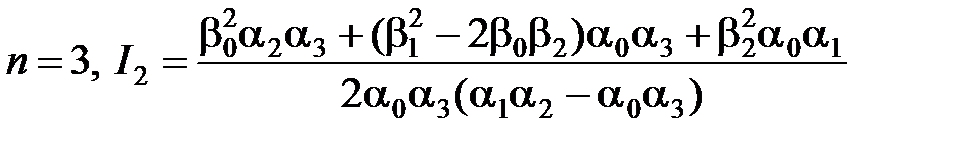 .
.
Наряду с оценками 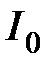 ,
, 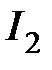 употребляются и более сложные интегральные оценки, учитывавшие не только само отклонение
употребляются и более сложные интегральные оценки, учитывавшие не только само отклонение 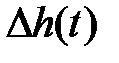 , но и его производные.
, но и его производные.
При использовании интегральных оценок можно выделить два направления: анализ системы – получение оценки для заданной системы и синтез системы – минимизация оценки по каким-либо параметрам.
25. Частотные оценки качества.
Частотные оценки качества базируются на связи частотных и временных характеристик системы управления, в частности, на связи переходной функции замкнутой системы 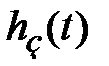 и вещественной частотной характеристики
и вещественной частотной характеристики 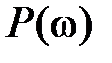 (4.13). Из (4.13) можно получить две категории оценок, одна из которых строго обоснована и математически доказана, а другая получена на основе построения большого числа переходных процессов для различных
(4.13). Из (4.13) можно получить две категории оценок, одна из которых строго обоснована и математически доказана, а другая получена на основе построения большого числа переходных процессов для различных 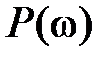 и осреднения полученных результатов.
и осреднения полученных результатов.
Рассмотрим первую группу оценок.
1. Начальное значение Р(0) и конечное значение 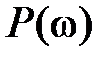 связаны с конечным значением
связаны с конечным значением 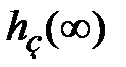 и начальным
и начальным 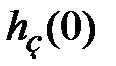 соотношениями
соотношениями
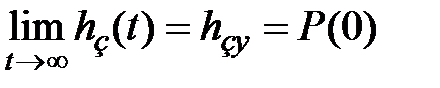 ,
, 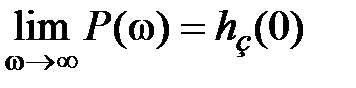 . (7.17)
. (7.17)
Эти свойства фактически являются следствием теорем о конечном и начальном значениях оригинала в преобразовании Лапласа. Так как для астатических систем 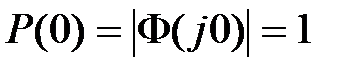 , а для статических
, а для статических 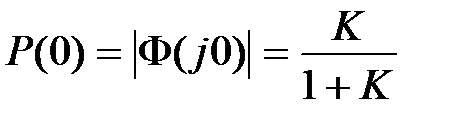 , то
, то
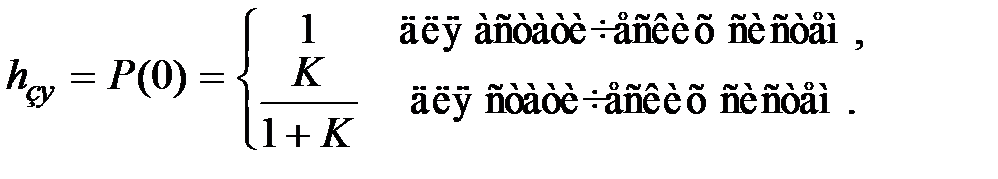
2. Сжатию характеристики 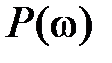 по оси
по оси 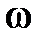 соответствует пропорциональное растяжение характеристики
соответствует пропорциональное растяжение характеристики 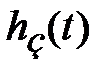 по оси t. Это свойство является следствием из свойств преобразования Фурье об изменении масштаба по оси ординат. Приведенное свойство дает важную сравнительную оценку переходных процессов в системах: более пологим характеристикам
по оси t. Это свойство является следствием из свойств преобразования Фурье об изменении масштаба по оси ординат. Приведенное свойство дает важную сравнительную оценку переходных процессов в системах: более пологим характеристикам 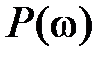 (более растянутым вдоль оси
(более растянутым вдоль оси 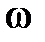 ) соответствуют более быстро протекающие переходные процессы, а более крутым или сжатым вдоль оси
) соответствуют более быстро протекающие переходные процессы, а более крутым или сжатым вдоль оси 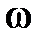 – замедленные процессы. Соответственно следует ожидать, что для первого случая время регулирования
– замедленные процессы. Соответственно следует ожидать, что для первого случая время регулирования 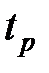 будет меньше, чем для второго.
будет меньше, чем для второго.
3. Достаточным условием того, чтобы перерегулирование  в системе не превышало 18 %, является выполнение соотношений
в системе не превышало 18 %, является выполнение соотношений
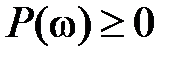 ,
,  , (7.18)
, (7.18)
т.е. 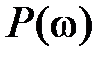 является невозрастающей положительной функцией частоты.
является невозрастающей положительной функцией частоты.
4. Достаточным условием монотонности переходного проходного процесса, т.е. 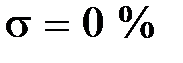 , является выполнение соотношений
, является выполнение соотношений
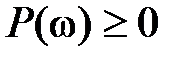 ,
, 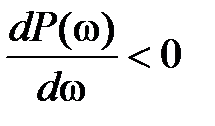 . (7.19)
. (7.19)
На рис. 7.4, а представлены две вещественные частотные характеристики, из которых для первой 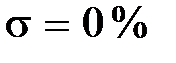 , а для второй –
, а для второй – 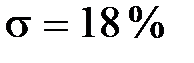 .
.
Рис. 7.4
5. Если характеристическое уравнение замкнутой системы 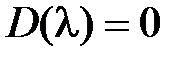 имеет чисто мнимый корень
имеет чисто мнимый корень 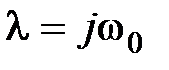 , то характеристика
, то характеристика 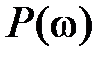 при
при 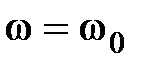 имеет разрыв непрерывности, что соответствует незатухающей гармонической составляющей с частотой
имеет разрыв непрерывности, что соответствует незатухающей гармонической составляющей с частотой 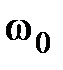 в переходном процессе
в переходном процессе 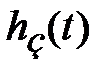 . График такой характеристики представлен на рис. 7.4, б. Поэтому если характеристика вблизи некоторой частоты
. График такой характеристики представлен на рис. 7.4, б. Поэтому если характеристика вблизи некоторой частоты 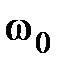 имеет резкий перепад и большие пики, то следует ожидать наличия в переходной функции медленно затухающей гармонической составляющей частоты
имеет резкий перепад и большие пики, то следует ожидать наличия в переходной функции медленно затухающей гармонической составляющей частоты 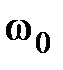 . Такой случай представлен на рис. 7.4, в.
. Такой случай представлен на рис. 7.4, в.
Оценки второй группы, как указывалось выше, имеют приближенный и в значительной степени эмпирический характер.
На рис. 7.5, а, б показаны случаи аппроксимации вещественной характеристики 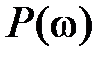 соответственно одной и суммой двух трапецеидальных характеристик.
соответственно одной и суммой двух трапецеидальных характеристик.
Рис. 7.5
Для случая, изображенного на рис. 7.5, а, время регулирования 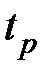 оценивается по неравенству
оценивается по неравенству
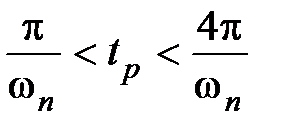 . (7.20)
. (7.20)
Для случая аппроксимации в виде суммы двух трапеций (см. рис. 7.5, б) время регулирования 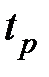 и перерегулирования
и перерегулирования  более сложным образом зависит от параметров аппроксимирующих трапеций.
более сложным образом зависит от параметров аппроксимирующих трапеций.
На рис. 7.6 представлены графики зависимостей 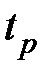 и
и  от
от 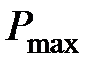 при
при 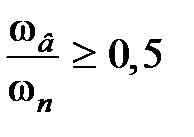 ,
, 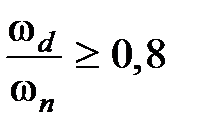 ;
; 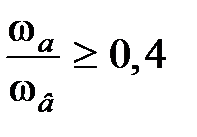 .
.
| | На этом рисунке время регулирования 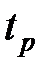 построено в относительных единицах, где построено в относительных единицах, где 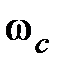 – частота среза разомкнутой системы.
Оценку (7.20) приближенно можно применять и для системы, имеющей произвольную вещественную характеристику – частота среза разомкнутой системы.
Оценку (7.20) приближенно можно применять и для системы, имеющей произвольную вещественную характеристику 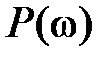 . При этом величину . При этом величину 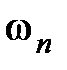 следует выбирать такой, после которой следует выбирать такой, после которой 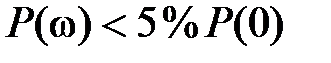 .
для характеристики рис. 7.5, б справедлива такая оценка перерегулирования: .
для характеристики рис. 7.5, б справедлива такая оценка перерегулирования: 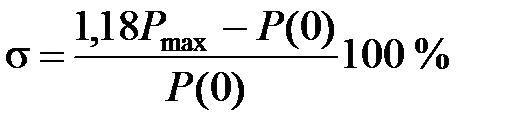 . .
|
Наряду с оценками качества системы по переходной функции 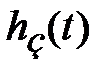 широкое распространение получили оценки качества системы при отработке гармонических входных сигналов. Особенно это касается исследования следящих систем, для которых изменяющиеся по амплитуде и знаку входные сигналы наиболее характерны. При таком подходе удобнее пользоваться АЧХ замкнутой системы
широкое распространение получили оценки качества системы при отработке гармонических входных сигналов. Особенно это касается исследования следящих систем, для которых изменяющиеся по амплитуде и знаку входные сигналы наиболее характерны. При таком подходе удобнее пользоваться АЧХ замкнутой системы 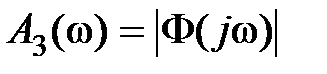 , типичный график которой представлен на рис. 7.7.
, типичный график которой представлен на рис. 7.7.
| | Величина 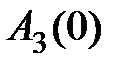 для астатических систем равна 1, а для статических для астатических систем равна 1, а для статических 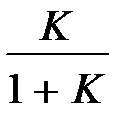 и при большом K близка к единице. Частота и при большом K близка к единице. Частота 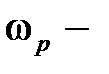 резонансная частота, при которой резонансная частота, при которой 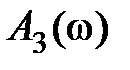 достигает максимального значения достигает максимального значения 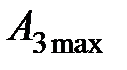 . Частота . Частота 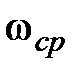 – частота среза замкнутой системы, при которой – частота среза замкнутой системы, при которой 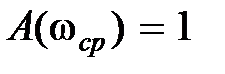 ( ( 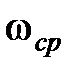 не совпадает с частотой среза разомкнутой системы, которая не совпадает с частотой среза разомкнутой системы, которая
|
обозначается 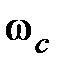 ). Интервал частот
). Интервал частот 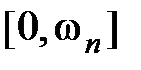 определяет полосу пропускания системы. Величина
определяет полосу пропускания системы. Величина 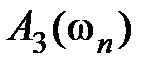 может задаваться из условий точности воспроизведения гармонического сигнала (см. подразд. 6.3).
может задаваться из условий точности воспроизведения гармонического сигнала (см. подразд. 6.3).
Частота 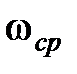 косвенно характеризует время регулирования в замкнутой системе, которое оценивается величиной
косвенно характеризует время регулирования в замкнутой системе, которое оценивается величиной 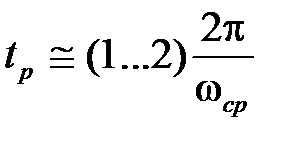 .
.








