Выражение (7.4) и соответственно величина характеризуют предельное быстродействие системы, поэтому иногда величину называют еще мерой быстродействия системы.
Из рассмотренного выше следует, что доминирующее влияние на характер переходного процесса оказывают ближайшие к мнимой оси корни. Если ближайшими являются комплексно-сопряженные корни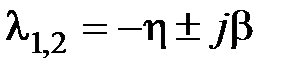 
, то наряду со степенью устойчивости вводят в рассмотрение колебательность системы (колебательность переходного процесса) 
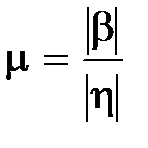. Паре комплексно-сопряженных корней в (7.1) соответствует составляющая
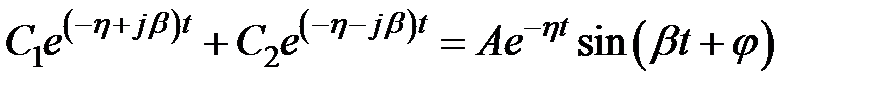, (7.5)
где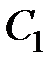 
, 
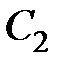– комплексно-сопряженные величины; A, 
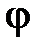– действительные величины.
Составляющая (7.5) носит колебательный характер. Период колебания определяется величиной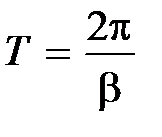 
. Уменьшение амплитуды в (7.5) за период Т будет равно 
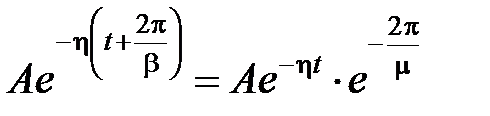, т.е. определяться величиной 
.
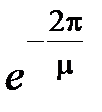Перерегулирование в % может быть оценено по формуле
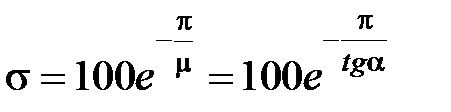. (7.6)
С увеличением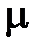 
увеличивается число колебаний за время регулирования и возрастает перерегулирование. Величина 
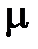носит качественный характер и является оценкой переходного процесса сверху, поэтому в действительности переходной процесс может иметь лучшие показатели.
Характер переходного процесса в значительной степени зависит от корней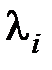 
характеристического уравнения, т.е. от полюсов передаточной функции 
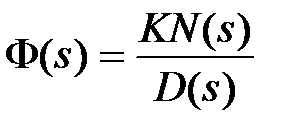замкнутой системы. Однако на величину амплитуды переходных составляющих будут влиять и нули передаточной функции. Пусть полином N(s) имеет m нулей 
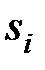, тогда 
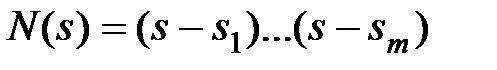и выражение (7.1) примет вид 
.
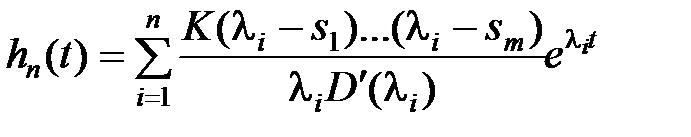Очевидно, если какой-то полюс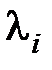 
будет близок (или в идеальном случае равен) нулю передаточной функции, то составляющая, соответствующая корню 
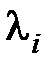, будет мала по амплитуде (или равна нулю).
Впервые корневые оценки качества переходных процессов для систем третьего порядка были предложены в работе И. А. Вышнеградского (1876), положившей начало развитию теории автоматического управления.
Характеристическое уравнение системы третьего порядка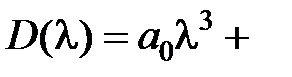 
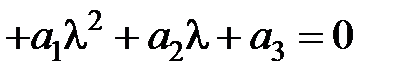путем замены переменной приводится к виду
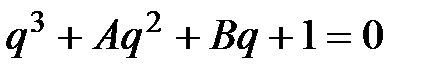, (7.7)
где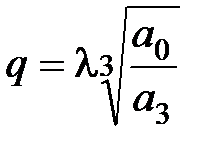 
, 
, 
.
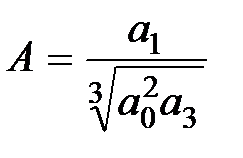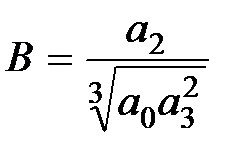Коэффициенты А, В – параметры Вышнеградского – являются комбинацией коэффициентов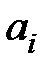 
и в конечном итоге зависят от реальных параметров системы. Условие асимптотической устойчивости для уравнения (7.7) несложно получить с помощью критерия Гурвица, оно имеет вид АВ > 1. В области устойчивости, ограниченной гиперболой АВ = 1 в плоскости параметров А, В, нанесем кривые, разделяющие область устойчивости на области с одинаковым расположением корней характеристического уравнения (7.7).
На рис. 7.2 представлена диаграмма Вышнеградского, где для каждой области показано расположение корней и вид переходного процесса.
Таким образом, выбирая из диаграммы требуемый вид переходного процесса, можно найти необходимые значения параметров А, В или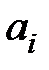 
.
В заключение отметим ряд простых случаев, когда получены оценки степени устойчивости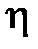 
и соответственно быстродействия системы. Рассмотрим систему управления стандартной структуры, изображенной на рис. 3.1. Пусть передаточная функция объекта управления 
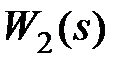имеет вид 
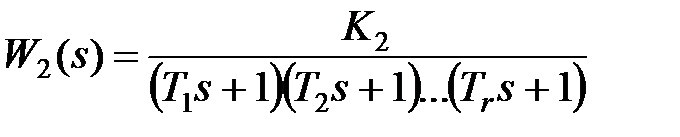, где 
.
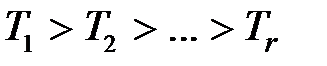рис. 7.2
Передаточную функцию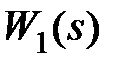 
будем рассматривать как передаточную функцию регулятора (управляющего устройства). Рассмотрим три случая закона управления: интегральный 
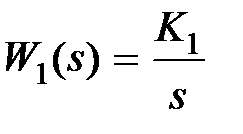, пропорциональный 
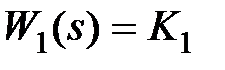, пропорционально-интегральный 
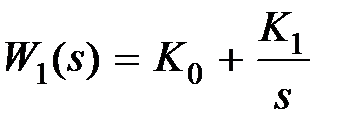. Быстродействие объекта управления может быть охарактеризовано величиной 
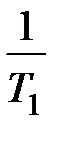. Доказано, что для интегрального закона управления быстродействие замкнутой системы, характеризуемое величиной степени устойчивости 
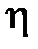, не будет превосходить быстродействия объекта, т.е. 
.
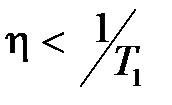Для пропорционального и пропорционально-интегрального законов управления быстродействие замкнутой системы управления может превосходить быстродействие объекта управления, но будет ограничено неравенством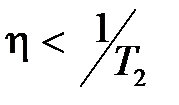 
.
Приведенный частный результат распространяется на более общий
случай: астатические системы уступают по быстродействию системам статическим.
24. Интегральные оценки качества.
Интегральные оценки качества являются интегралами по времени от некоторых функций координат системы (выходной координаты, сигнала ошибки) и оценивают одним числом как величину отклонения, так и время регулирования. В качестве исследуемого процесса обычно выбирается разность между установившимся процессом в системе и самой координатой. Рассмотрим замкнутую систему управления стандартной структуры, на вход которой поступает единичный ступенчатый сигнал υ(t) = 1[t]. Тогда реакция системы будет представлять собой переходную функцию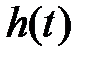 
, которая в соответствии с (4.10) определяется выражением 
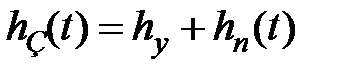, где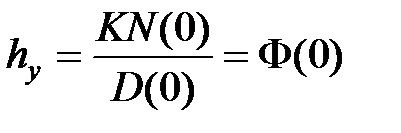 
– установившаяся составляющая; 
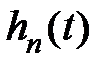– переходная составляющая, характеризующая переходной процесс.
Введем отклонение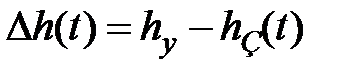 
процесса 
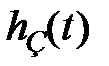от его установившегося значения. Очевидно, что 
.
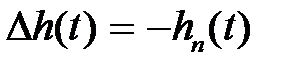Простейшими интегральными оценками качества являются:
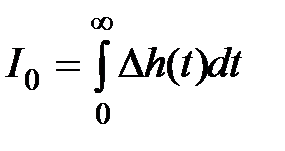, (7.8)
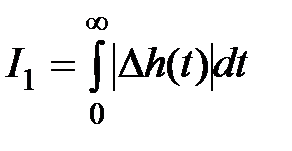, (7.9)
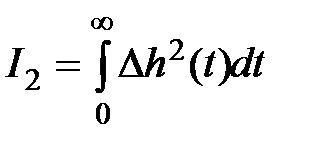. (7.10)