Если , то . В статической системе и , для системы с астатизмом первого порядка имеем и , а
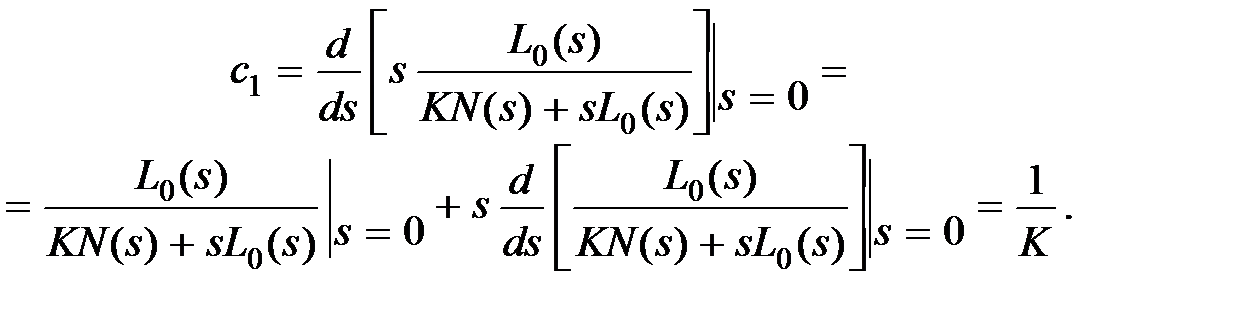
Аналогично можно показать, что для астатической системы с астатизмом 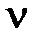 -го порядка
-го порядка 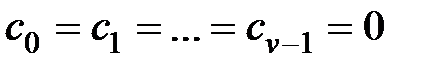 ,
, 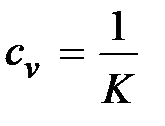 .
.
Коэффициент 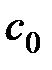 называют коэффициентом статической ошибки,
называют коэффициентом статической ошибки, 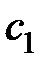 – коэффициентом скоростной ошибки,
– коэффициентом скоростной ошибки, 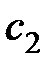 – коэффициентом ошибки по ускорению. Из (6.8) следует, что если
– коэффициентом ошибки по ускорению. Из (6.8) следует, что если 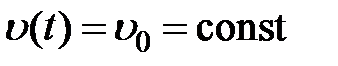 , то
, то 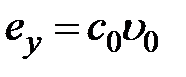 , если
, если 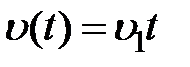 , то
, то 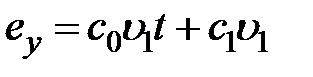 .
.
В общем случае формула (6.9) редко используется для вычисления 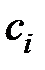 . На практике применяется другой способ. Разложим передаточную функцию
. На практике применяется другой способ. Разложим передаточную функцию 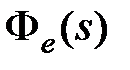 в ряд Маклорена при s = 0:
в ряд Маклорена при s = 0:
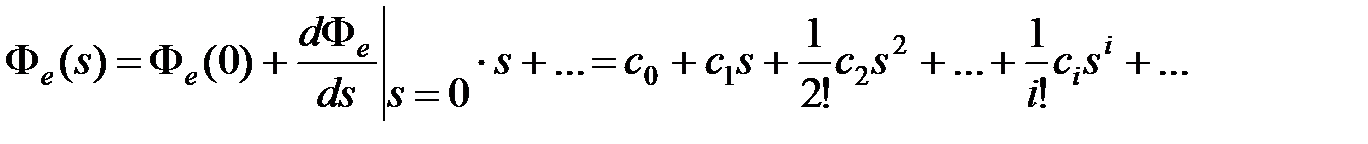 . (6.10)
. (6.10)
С другой стороны, так как 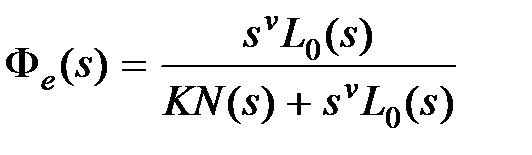 есть отношение полиномов, то деля полином числителя на полином знаменателя, получим ряд
есть отношение полиномов, то деля полином числителя на полином знаменателя, получим ряд
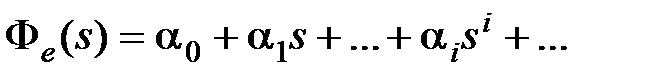 . (6.11)
. (6.11)
Приравнивая коэффициенты при одинаковых степенях s в (6.10), (6.11), получим
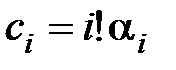 . (6.12)
. (6.12)
Величина коэффициентов ошибок в конечном итоге определяет величину ошибки в системе. Из изложенного выше вновь следует, что величины 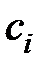 будут тем меньше, чем выше порядок астатизма системы и чем больше величина коэффициента усиления K разомкнутой системы.
будут тем меньше, чем выше порядок астатизма системы и чем больше величина коэффициента усиления K разомкнутой системы.
22. Установившаяся ошибка при гармоническом сигнале.
Если главная передаточная функция замкнутой системы имеет вид 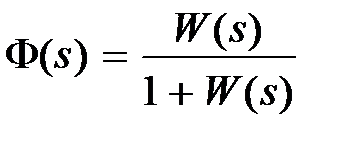 , то при входном сигнале
, то при входном сигнале 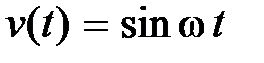 выходной сигнал в установившемся режиме
выходной сигнал в установившемся режиме 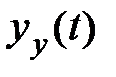 будет определяться выражением
будет определяться выражением
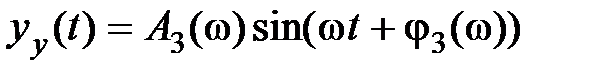 , (6.13)
, (6.13)
где 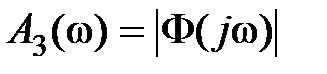 ,
, 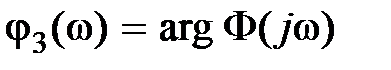 .
.
Аналогично, зная 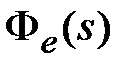 , можно найти закон изменения ошибки в установившемся режиме при гармоническом входном сигнале
, можно найти закон изменения ошибки в установившемся режиме при гармоническом входном сигнале 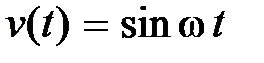 :
:
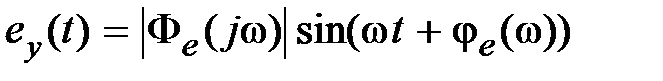 , (6.14)
, (6.14)
где 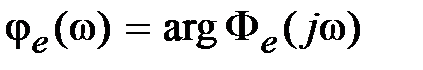 .
.
Выражения (6.13), (6.14) позволяют оценить ошибки воспроизведения гармонического сигнала в установившемся режиме. Из этих выражений следует, что кроме ошибки воспроизведения амплитуды входного гармонического сигнала существуют и постоянные фазовые ошибки, которые определяются видом фазочастотных характеристик замкнутой системы. Обычно при анализе точности систем управления их не рассматривают, ограничиваясь лишь анализом ошибок воспроизведения амплитуды.
Из (6.13), (6.14) можно получить ошибки воспроизведения амплитуды гармонического сигнала на заданной частоте, равные
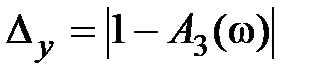 , (6.15)
, (6.15)
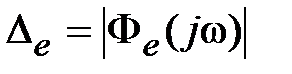 , (6.16)
, (6.16)
первая из которых характеризует разность между максимальными значениями амплитуды входного и выходного сигналов, а вторая – максимальную величину ошибки 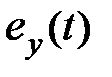 . Очевидно, всегда
. Очевидно, всегда 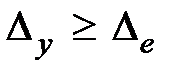 . Так как
. Так как 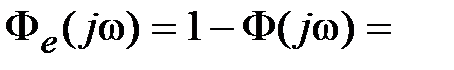
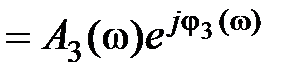 то
то 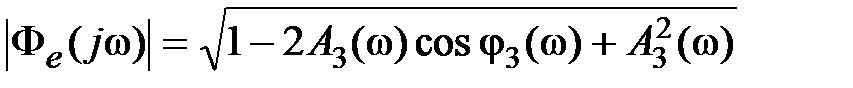 . Если
. Если 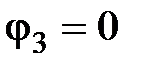 , то
, то 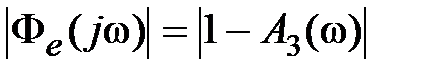 . Таким образом, при малых фазовых сдвигах на заданной частоте
. Таким образом, при малых фазовых сдвигах на заданной частоте 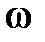 оценки (6.15) и (6.16) будут близки между собой. Это обычно выполняется в диапазоне низких частот.
оценки (6.15) и (6.16) будут близки между собой. Это обычно выполняется в диапазоне низких частот.
На рис. 6.2 представлен типичный вид АЧХ замкнутой системы 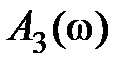 для случая астатической системы, при этом
для случая астатической системы, при этом 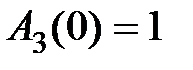 . В случае статической системы
. В случае статической системы 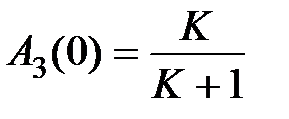 . На рисунке заштрихованная область соответствует величинам ошибок
. На рисунке заштрихованная область соответствует величинам ошибок 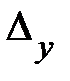 .
.
Рис. 6.2
Под полосой пропускания системы понимают диапазон частот 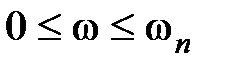 , при котором ошибка
, при котором ошибка 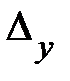 будет меньше некоторой заданной
будет меньше некоторой заданной  , т.е.
, т.е. 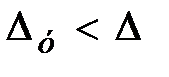 . Иногда полосу пропускания определяют как диапазон частот
. Иногда полосу пропускания определяют как диапазон частот 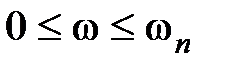 , при котором выполняется условие
, при котором выполняется условие 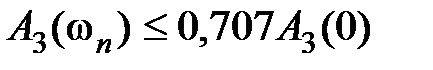 .
.
Полоса пропускания является важной характеристикой системы. С одной стороны, чем шире полоса пропускания, тем с меньшими ошибками система воспроизводит управляющие сигналы. Однако, с другой стороны, увеличение 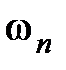 приводит к тому, что система становится чувствительной к влиянию высокочастотных помех.
приводит к тому, что система становится чувствительной к влиянию высокочастотных помех.
Из выражения (6.16) можно получить приближенные оценки величины ошибки 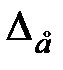 . Так как
. Так как 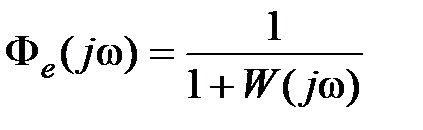 , то для статической системы
, то для статической системы 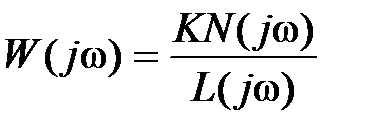 и при достаточно низких частотах можно полагать
и при достаточно низких частотах можно полагать 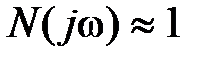 ,
, 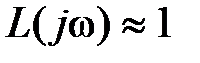 ,
, 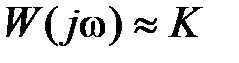 , откуда имеем
, откуда имеем
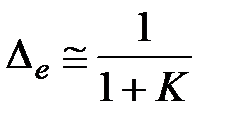 . (6.17)
. (6.17)
Для астатической системы 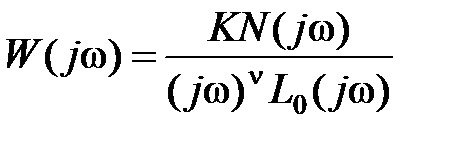 и при низких частотах
и при низких частотах 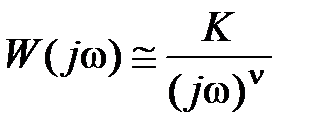 , откуда получим
, откуда получим
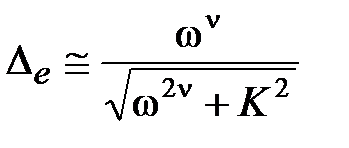 . (6.18)
. (6.18)
Если выполняется условие 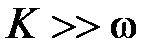 , то формула (6.18) принимает вид
, то формула (6.18) принимает вид
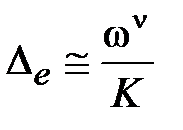 . (6. 19)
. (6. 19)
Из (6.17)–(6.19) видно, что ошибка системы обратно пропорциональна коэффициенту усиления разомкнутой системы.
Итак, для повышения точности САУ следует увеличивать коэффициент усиления разомкнутой системы либо увеличивать порядок астатизма. Однако это будет приводить в общем случае к ухудшению устойчивости. Таким образом, требования к точности системы и ее устойчивости являются противоречивыми.
23. Корневые оценки качества.
Переходная функция замкнутой системы как реакция системы на единичный скачок по положению вычисляется в соответствии с выражением
(4.11), в котором второе слагаемое в виде суммы определяет переходную
составляющую
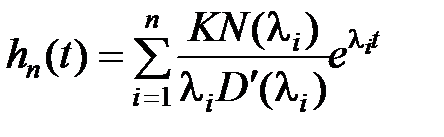 , (7.1)
, (7.1)
a 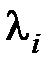 – различные корни характеристического уравнения замкнутой системы
– различные корни характеристического уравнения замкнутой системы 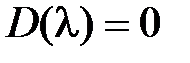 .
.
Если 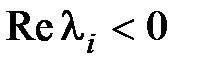 ,
, 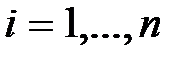 , то
, то 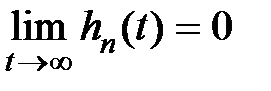 , т.е. с течением времени переходная составляющая затухает.
, т.е. с течением времени переходная составляющая затухает.
В выражении (7.1) перейдем к модулям в левой и правой частях:
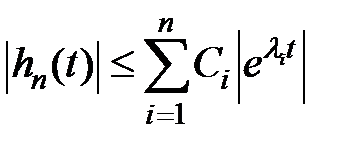 , (7.2)
, (7.2)
где 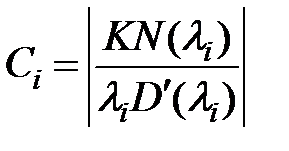 .
.
Обозначим расстояние от мнимой оси до ближайших действительного корня (рис. 7.1, а) или пары комплексно-сопряженных корней (рис. 7.1, б) на плоскости корней 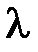 через
через 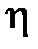 .
.
Рис. 7.1
Величину 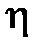 будем называть степенью устойчивости. Очевидно, что
будем называть степенью устойчивости. Очевидно, что 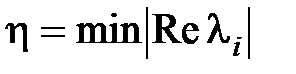 . Так как
. Так как 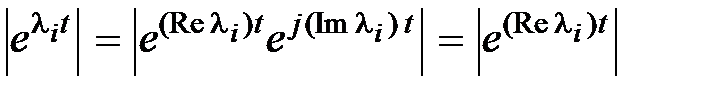 , то для любого множителя
, то для любого множителя 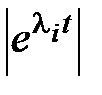 в (7.2) будет справедлива оценка
в (7.2) будет справедлива оценка 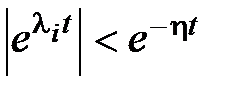 . Таким образом, (7.2) равносильно выражению
. Таким образом, (7.2) равносильно выражению
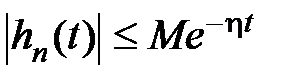 , а
, а 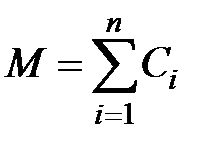 . (7.3)
. (7.3)
Из (7.3) следует, что переходная составляющая 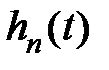 затухает быстрее, чем экспонента с показателем –
затухает быстрее, чем экспонента с показателем – 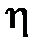 . Если принять время регулирования
. Если принять время регулирования 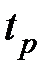 как время, начиная с которого
как время, начиная с которого 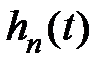 войдет в 5 % трубку от начального значения, то из (7.3) получим
войдет в 5 % трубку от начального значения, то из (7.3) получим 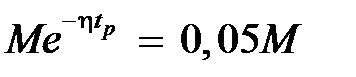 , откуда
, откуда
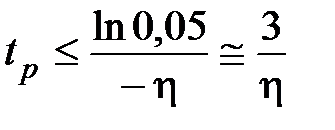 . (7.4)
. (7.4)








