Ошибку будем называть статической ошибкой системы.
При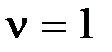 
(система с астатизмом первого порядка) вычислим ошибку при воздействиях 
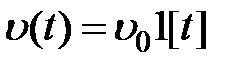и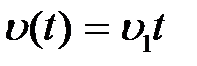 
. Подставляя передаточную функцию 
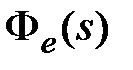и изображение входного сигнала в (6.2), получим соответственно для первого и второго типов входного сигнала
, 
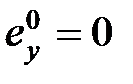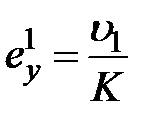, (6.4)
где ошибку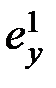 
будем называть ошибкой по скорости (скоростной ошибкой).
При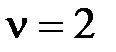 
и входных сигналах 
, 
, 
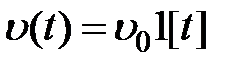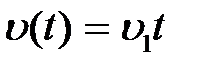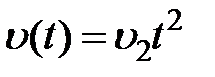соответственно получим выражения ошибок:
, 
, 
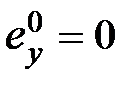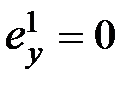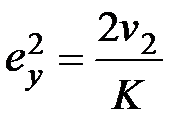, (6.5)
где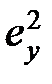 
– ошибка системы по ускорению.
При воздействии вида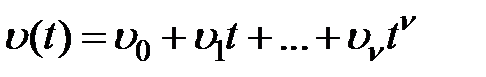 
для системы с астатизмом 
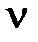-го порядка получаем
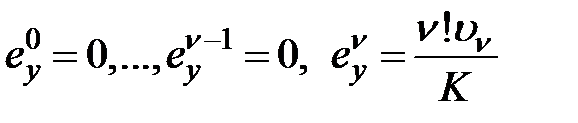. (6.6)
Из приведенных выражений следует, что ошибки в системе уменьшаются с ростом порядка астатизма системы и увеличением общего коэффициента усиления K.
На рис. 6.1 показаны переходные процессы в различных системах при отработке скачка по положению и скорости: кривая 1 – для статической системы, 2 – для системы с астатизмом первого порядка, 3 – для системы с астатизмом второго порядка.
Рис. 6.1
21. Установившаяся ошибка при производном сигнале.
Обозначим весовую функцию замкнутой системы по ошибке через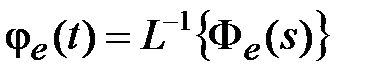 
. Тогда соотношению 
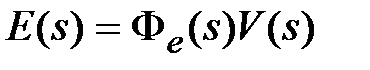во временной области будет соответствовать свертка 
.
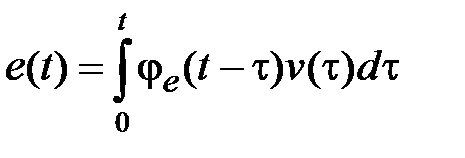Так как нас интересует установившаяся ошибка после затухания переходной составляющей, то отнесем нижний предел интегрирования, соответствующий моменту подачи входного сигнала, в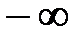 
. В этом случае получим выражение, справедливое для установившегося значения сигнала ошибки: 
.
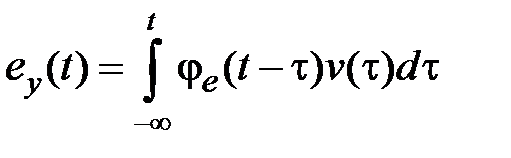Заменив переменную интегрирования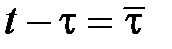 
, получим
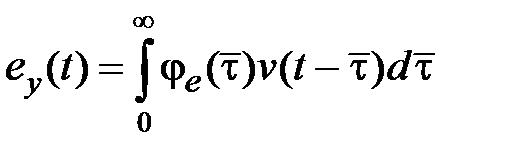. (6.7)
Полагая функцию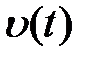 
аналитической, разложим ее в ряд Тейлора при 
: 
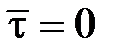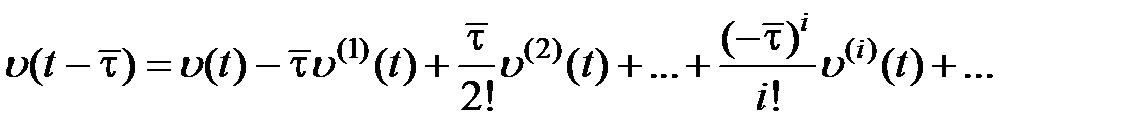и подставим полученный ряд в (6.7). В результате получим
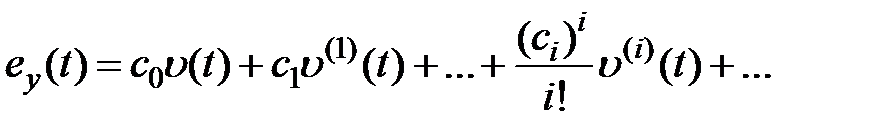, (6.8)
где коэффициенты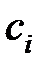 
определяются выражением 
.
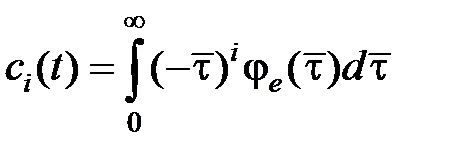Так как передаточная функция замкнутой системы по ошибке есть прямое преобразование Лапласа от весовой функции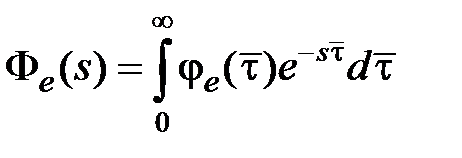 
, то очевидно соотношение
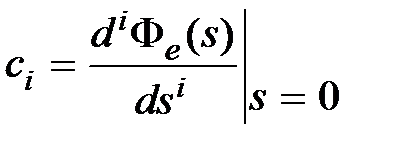. (6.9)
Коэффициенты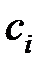 
носят название коэффициентов ошибок и характеризуют, с каким весом функция 
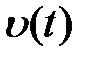и ее производные входят в общее выражение для установившейся ошибки (6.8). Если входной сигнал изменяется достаточно медленно, то в выражении (6.8) можно ограничиться конечным числом членов ряда.