В комплексной плоскости корней корни интерпретируются как соответствующие точки. Если корень лежит слева от мнимой оси, т. е. , будем называть его л eвым ко pн eм, если – п pавым.
Пусть 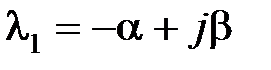 ,
,  – левый корень, тогда составляющая
– левый корень, тогда составляющая  в (4.4) при
в (4.4) при  будет затухать и стремиться
будет затухать и стремиться
к 0, а в случае правого корня 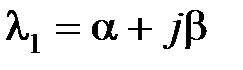 – наоборот возрастать до бесконечности. Таким образом, при различных корнях характеристического уравнения, если все корни левые,
– наоборот возрастать до бесконечности. Таким образом, при различных корнях характеристического уравнения, если все корни левые, 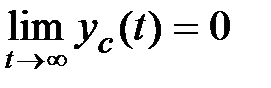 , что соответствует факту асимптотической устойчивости системы. Если хотя бы один корень правый (
, что соответствует факту асимптотической устойчивости системы. Если хотя бы один корень правый ( 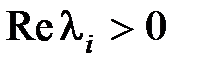 ), то
), то 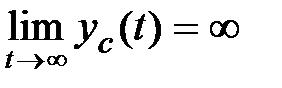 и система будет неустойчива. Если для всех различных корней справедливо соотношение
и система будет неустойчива. Если для всех различных корней справедливо соотношение 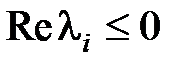 , то в свободной составляющей появятся слагаемые, которые будут либо постоянными (нулевой корень), либо будут изменяться по гармоническому закону (чисто мнимые корни), и составляющая
, то в свободной составляющей появятся слагаемые, которые будут либо постоянными (нулевой корень), либо будут изменяться по гармоническому закону (чисто мнимые корни), и составляющая 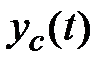 будет ограничена, что соответствует нейтральной системе.
будет ограничена, что соответствует нейтральной системе.
В случае кратного корня 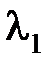 , если
, если 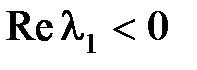 ,
, 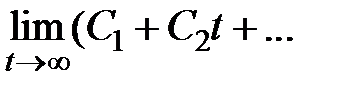
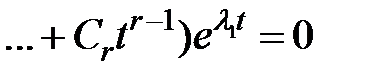 , так как при любом
, так как при любом 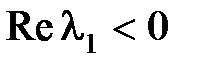 функция
функция 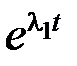 затухает быстрее, чем возрастает функция в скобках. Если же
затухает быстрее, чем возрастает функция в скобках. Если же 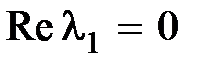 , то это утверждение не правомерно.
, то это утверждение не правомерно.
Таким образом, необходимым и достаточным условием асимптотической устойчивости линейной системы, описываемой уравнением (5.1), является выполнение соотношения 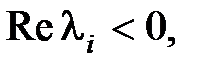
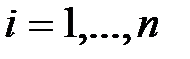 . Система будет просто устойчива, если
. Система будет просто устойчива, если 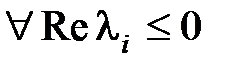 и среди корней, лежащих на мнимой оси, нет кратных. Система будет неустойчива, если имеется хотя бы один корень, для которого
и среди корней, лежащих на мнимой оси, нет кратных. Система будет неустойчива, если имеется хотя бы один корень, для которого 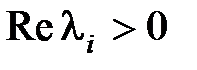 , или хотя бы один кратный корень, лежащий на мнимой оси.
, или хотя бы один кратный корень, лежащий на мнимой оси.
Суждение об устойчивости можно сделать, найдя корни характеристического уравнения замкнутой системы
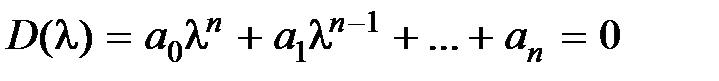 . (5.2)
. (5.2)
Эту задачу можно упростить, так как фактически нам достаточно знать лишь расположение корней в плоскости корней относительно мнимой оси, которую называют границей устойчивости. Выделяют три типа границы устойчивости: aп epиодич eского типа, которая характеризуется нулевым корнем характеристического уравнения, кол eбательного типа, что соответствует наличию пары чисто мнимых корней, и границу, соответствующую бесконечно удаленному корню ( 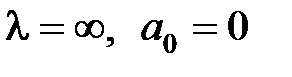 (5.2)). Если все корни уравнения (5.2) лежат слева от мнимой оси, т.е.
(5.2)). Если все корни уравнения (5.2) лежат слева от мнимой оси, т.е. 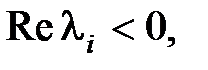
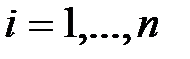 , то характеристический полином
, то характеристический полином 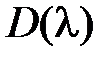 будем называть полиномом Гу pвица, или гу pвиц eвым полиномом.
будем называть полиномом Гу pвица, или гу pвиц eвым полиномом.
Определение расположения корней уравнения (5.2) относительно мнимой оси без их непосредственного вычисления производят на основе критериев устойчивости, которые делятся на две группы: алгебраические и частотные.
17. Алгебраические критерии Гурвица.
К алгебраическим критериям устойчивости относят те, которые позволяют судить об устойчивости системы по коэффициентам уравнения (5.2). необходимым условием устойчивости линейной системы (5.1) является положительность коэффициентов характеристического уравнения (5.2), т.е.
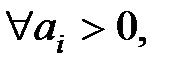
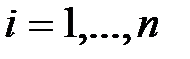 . (5.3)
. (5.3)
Докажем этот критерий. Пусть уравнение (5.2) имеет n корней 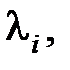
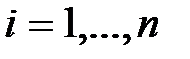 , тогда полином
, тогда полином 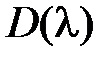 можно пo теореме Безу представить в виде
можно пo теореме Безу представить в виде 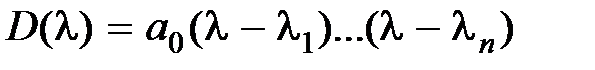 . Если
. Если 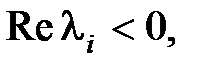
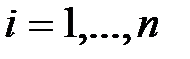 , то произведение n сомножителей
, то произведение n сомножителей 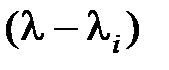 всегда даст полином n-й степени с положительными коэффициентами, и с учетом
всегда даст полином n-й степени с положительными коэффициентами, и с учетом 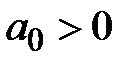 получим (5.3).
получим (5.3).
Критерий является лишь необходимым, т.е. если среди 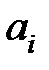 есть отрицательные коэффициенты, то система неустойчива; если все
есть отрицательные коэффициенты, то система неустойчива; если все 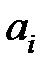 положительны, то система может быть как устойчивой, так и неустойчивой. В этом последнем случае требуется дальнейшее исследование.
положительны, то система может быть как устойчивой, так и неустойчивой. В этом последнем случае требуется дальнейшее исследование.
Рассмотрим критерий, дающий необходимые и достаточные условия устойчивости, предложенные немецким ученым А. Гурвицем в 1895 году. Предварительно из коэффициентов уравнения (5.2) сформируем матрицу Гурвица:
| | (5.4) |
Алгоритм ее формирования следующий. Сначала по главной диагонали слева направо выписываем коэффициенты 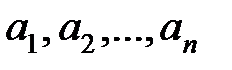 . Далее столбцы вверх от главной диагонали дополняются коэффициентами с возрастающими индексами, а вниз – с убывающими индексами. Коэффициенты с индексами больше
. Далее столбцы вверх от главной диагонали дополняются коэффициентами с возрастающими индексами, а вниз – с убывающими индексами. Коэффициенты с индексами больше
n и меньше нуля заменяются нулями. Последний столбец матрицы имеет все нулевые коэффициенты, кроме последнего 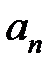 . Обозначим через
. Обозначим через 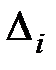 главные определители матрицы Гурвица, которые выделены в (5.4) штриховыми
главные определители матрицы Гурвица, которые выделены в (5.4) штриховыми
линиями: 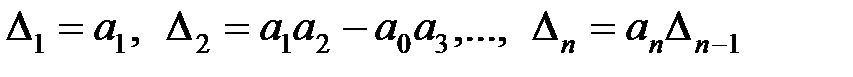 , где
, где 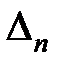 – определитель матрицы Гурвица.
– определитель матрицы Гурвица.
Крит epий Гу pвица. Необходимым и достаточным условием устойчивости линейной системы является при 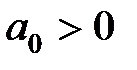 положительность всех определителей Гурвица:
положительность всех определителей Гурвица:
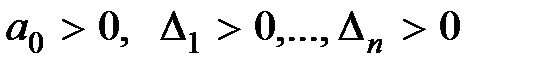 . (5.5)
. (5.5)
Для систем до 4-го порядка включительно, раскрывая определители Гурвица, можно получить необходимые и достаточные условия устойчивости:
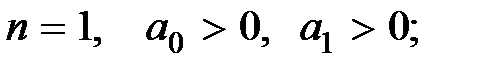 (5.6)
(5.6)
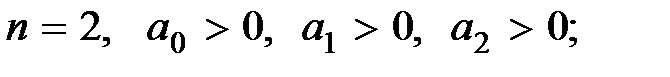 (5.7)
(5.7)
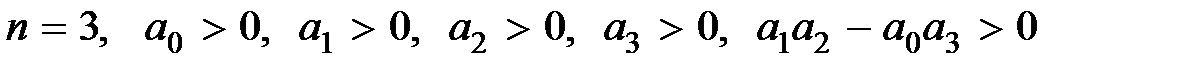 ; (5.8)
; (5.8)
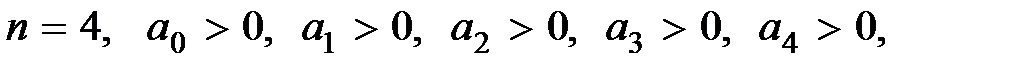
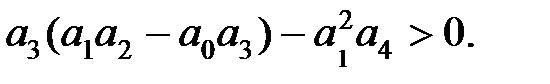 (5.9)
(5.9)
Из (5.6), (5.7) следует, что для системы первого и второго порядка необходимые условия совпадают с необходимыми и достаточными, а при n = 3 и 4 кроме необходимых условий следует соблюдать дополнительное неравенство. При n = 5 и 6 появляются два дополнительных неравенства, при n = 7 и 8 – три
и т.д. при аналитических исследованиях критерий Гурвица наиболее удобен для систем, порядок которых 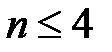 .
.
С помощью критерия Гурвица можно определить границы устойчивости. Если  и все определители Гурвица
и все определители Гурвица  , кроме последнего, больше нуля, то нарушение условий устойчивости будет при
, кроме последнего, больше нуля, то нарушение условий устойчивости будет при 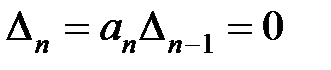 , откуда при
, откуда при 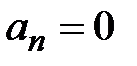 получаем границу устойчивости апериодического типа (появляется один нулевой корень), а при
получаем границу устойчивости апериодического типа (появляется один нулевой корень), а при 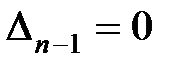 границу устойчивости колебательного типа (появляются два комплексно-сопряженных корня). При этом все остальные корни являются левыми. Граница устойчивости, соответствующая бесконечному корню, будет
границу устойчивости колебательного типа (появляются два комплексно-сопряженных корня). При этом все остальные корни являются левыми. Граница устойчивости, соответствующая бесконечному корню, будет 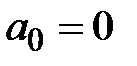 .
.
Одним из частных случаев критерия Гурвица является критерий Льенара–Шипара (1914), по которому для устойчивости системы необходимо и достаточно выполнение следующих неравенств:
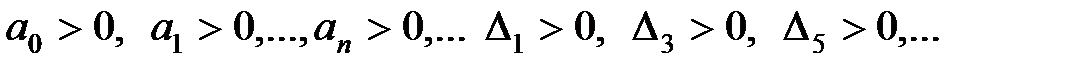
или
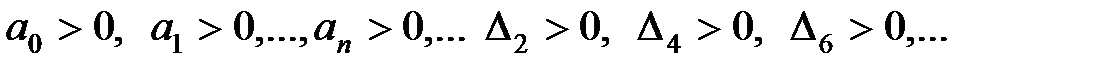 ,
,
т.е. при соблюдении необходимых условий устойчивости требуется положительность четных или нечетных определителей Гурвица.
Вторым распространенным алгебраическим критерием устойчивости, дающим необходимые и достаточные условия устойчивости, является критерий Рауса–Гурвица. Этот критерий более удобен при анализе устойчивости с помощью ПЭВМ.
На первом этапе составляется таблица Рауса, элементы которой образуются из коэффициентов характеристического полинома замкнутой системы 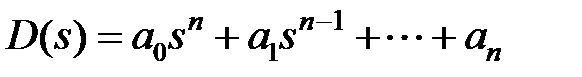 , в которой
, в которой  .
.
Таблица Рауса:
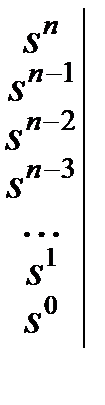
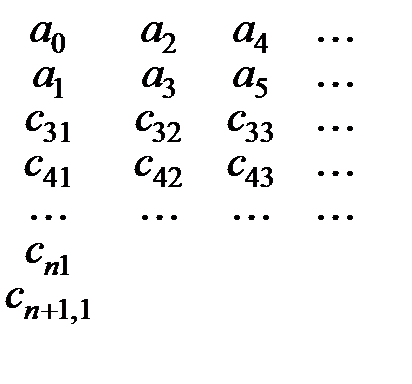 (5.10)
(5.10)
Первые две строки состоят из коэффициентов 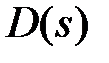 .
.
Коэффициенты последующих строк вычисляются так:
| (5.11) |
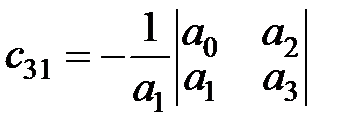 ;
; 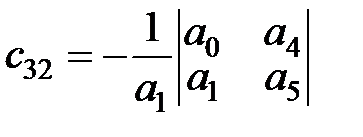 ; …
; …
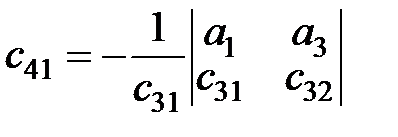 ;
; 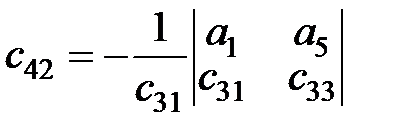 ; …
; …
и т.д.
Левый столбец записывается для наглядности.
По критерию Рауса–Гурвица система устойчива, если при 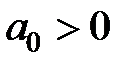 положительны все элементы первого столбца таблицы (
положительны все элементы первого столбца таблицы ( 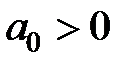 ,
, 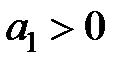 ,
, 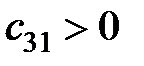 ,
, 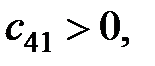 …).
…).
Число правых корней в случае неустойчивой САУ равно числу перемен знака элементов первого столбца. Если элемент какой-то строки первого столбца равен нулю, то САУ либо неустойчива, либо находится на границе устойчивости [6].
18. Критерии устойчивости Михайлова.
Этот критерий относится к группе частотных и был предложен в 1938 г. А. Михайловым. Он базируется на известном в теории функции комплексного переменного принципе аргумента. Характеристический полином замкнутой системы представим в виде 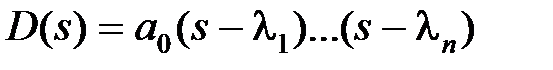 , где
, где 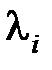 – корни уравнения
– корни уравнения 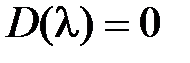 .
.
Сделаем замену 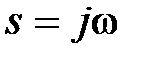 , тогда
, тогда 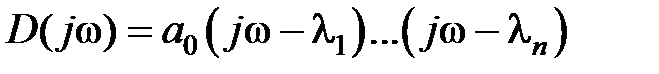 . Приращение аргумента вектора
. Приращение аргумента вектора 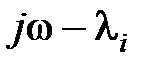 при изменении частоты
при изменении частоты 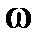 от
от 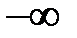 до
до 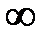 будет равно
будет равно  для левого корня и
для левого корня и 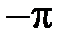 для правого корня (рис. 5.1). Приращение аргумента вектора
для правого корня (рис. 5.1). Приращение аргумента вектора 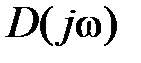 , имеющего
, имеющего  правых и
правых и 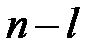 левых корней, будет равно
левых корней, будет равно 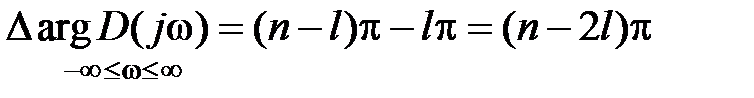 , а при изменении
, а при изменении 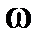 от 0 до
от 0 до 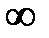 – в 2 раза меньше, т.е.
– в 2 раза меньше, т.е. 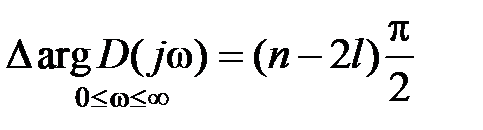 .
.
| | Из последнего выражения следует, что для устойчивой САУ 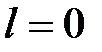 и и
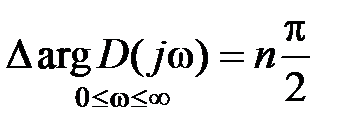 . (5.12)
Полином D(s) после замены . (5.12)
Полином D(s) после замены 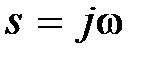 представляет собой комплексное число, действительная и мнимая части которого зависят от частоты представляет собой комплексное число, действительная и мнимая части которого зависят от частоты 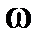 : :
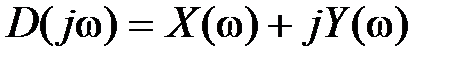 ,
где ,
где 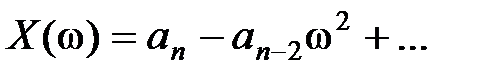 , ,
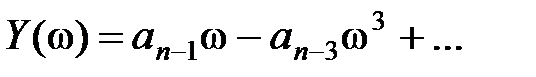 . .
|
Изменяя  от нуля до
от нуля до 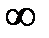 , на комплексной плоскости строится годограф, который называется к p ивой M и x айлова. При
, на комплексной плоскости строится годограф, который называется к p ивой M и x айлова. При 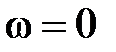 он всегда будет находиться на действительной оси в точке
он всегда будет находиться на действительной оси в точке 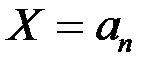 , а при
, а при 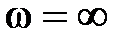 значения Х и Y равны
значения Х и Y равны 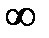 или
или 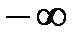 , т.е. годограф будет уходить в бесконечность в каком-либо квадранте комплексной плоскости.
, т.е. годограф будет уходить в бесконечность в каком-либо квадранте комплексной плоскости.
К p ит ep ий Ми x айлова. Для устойчивости линейной системы необходимо
и достаточно, чтобы приращение аргумента функции 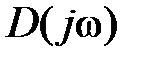 при изменении
при изменении
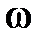 от нуля до
от нуля до 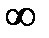 равнялось
равнялось 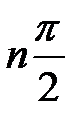 , что означает последовательное прохождение кривой Михайлова n квадрантов против часовой стрелки в комплексной
, что означает последовательное прохождение кривой Михайлова n квадрантов против часовой стрелки в комплексной
плоскости.
Обычно критерий Михайлова применяется после проверки необходимого условия устойчивости (5.3).
На рис. 5.2 представлен ряд кривых Михайлова для систем различного порядка.
Кривые 1, 2 соответствуют устойчивым системам при n = 3, 4 соответственно, кривая 3 – неустойчивой системе при 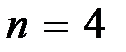 , так как нарушена последовательность прохождения квадратов комплексной плоскости.
, так как нарушена последовательность прохождения квадратов комплексной плоскости.
| | Рассмотрим определение с помощью кривой Михайлова границ устойчивости. Система будет находиться на границе устойчивости, если чисто мнимая величина 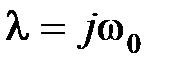 будет являться корнем уравнения будет являться корнем уравнения 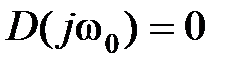 , т.е. кривая Михайлова должна проходить через начало координат. При этом при , т.е. кривая Михайлова должна проходить через начало координат. При этом при 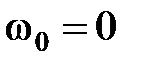 имеем апе- имеем апе-
|
риодическую границу, при 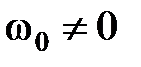 – колебательную,
– колебательную, 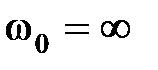 соответствует бесконечному корню. При этом следует проверить, чтобы все остальные корни были левыми. Такую проверку можно осуществить, исследуя соответствующий график кривой Михайлова в точке пересечения начала координат. Если малые деформации кривой приводят к устойчивой системе, то это соответствует границе устойчивости.
соответствует бесконечному корню. При этом следует проверить, чтобы все остальные корни были левыми. Такую проверку можно осуществить, исследуя соответствующий график кривой Михайлова в точке пересечения начала координат. Если малые деформации кривой приводят к устойчивой системе, то это соответствует границе устойчивости.
На рис. 5.3 представлены два годографа, проходящие через начало координат.
| | Для кривой 1 малые деформации ее в начале координат приведут к устойчивой системе, что соответствует границе устойчивости, а для кривой 2 система при малых деформациях графика все равно будет неустойчивой.
Пример 5.4. Передаточная функция разомкнутой системы имеет вид 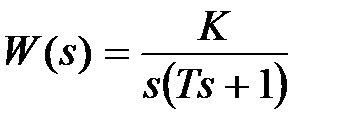 . Характеристический полином замкнутой системы будет . Характеристический полином замкнутой системы будет 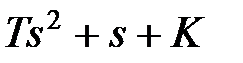 и соответственно и соответственно 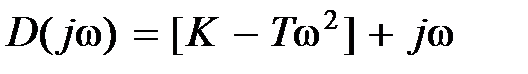 . При любом . При любом
|
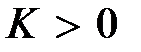 ,
, 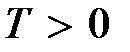 кривая Михайлова при
кривая Михайлова при 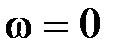 будет начинаться на действительной оси в точке с координатами (K, j0) и всегда проходить последовательно первый и второй квадранты комплексной области, так как мнимая часть
будет начинаться на действительной оси в точке с координатами (K, j0) и всегда проходить последовательно первый и второй квадранты комплексной области, так как мнимая часть 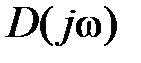 всегда положительна, а действительная с ростом W меняет знак с плюса на минус.
всегда положительна, а действительная с ростом W меняет знак с плюса на минус.
Система при любых K > 0, T > 0 всегда устойчива, что совпадает с результатом примера 5.1.
19. Критерии устойчивости Найквиста.
Критерий устойчивости Найквиста – это частотный критерий, предложенный в 1932 г. Найквистом. Он позволяет судить об устойчивости замкнутой системы управления по виду АФЧХ разомкнутой системы.
Пусть задана передаточная функция разомкнутой системы в виде 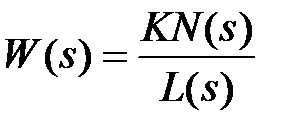 , где L(s) – полином степени n; N(s) – полином степени m,
, где L(s) – полином степени n; N(s) – полином степени m, 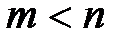 . Тогда ее АФЧХ будет
. Тогда ее АФЧХ будет 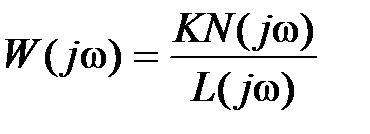 . Составим вспомогательную функцию
. Составим вспомогательную функцию 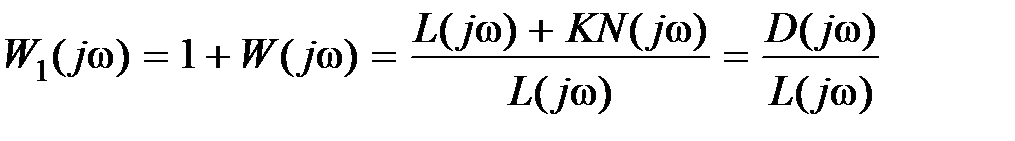 , где D(s) – характеристический полином замкнутой системы, степень которого будет n.
, где D(s) – характеристический полином замкнутой системы, степень которого будет n.
Предположим, что характеристическое уравнение разомкнутой системы 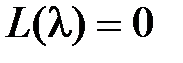 имеет l правых корней и
имеет l правых корней и 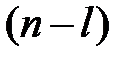 левых корней. Тогда приращение аргумента функции
левых корней. Тогда приращение аргумента функции 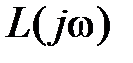 при изменении
при изменении 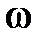 oт
oт 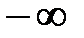 до
до 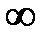 будет
будет 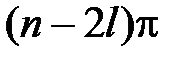 . Если система устойчива в замкнутом состоянии, то характеристическое уравнение замкнутой системы
. Если система устойчива в замкнутом состоянии, то характеристическое уравнение замкнутой системы 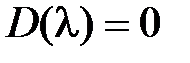 имеет n левых корней и приращение аргумента
имеет n левых корней и приращение аргумента 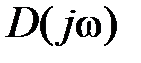 будет paвнo
будет paвнo 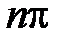 . Найдем приращение аргумента функции
. Найдем приращение аргумента функции 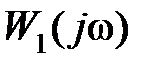 при изменении
при изменении 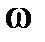 oт
oт 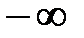 до
до  , которое будет в этом случае равно
, которое будет в этом случае равно
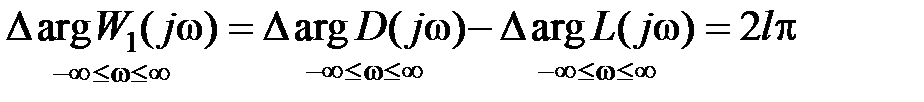 . (5.13)
. (5.13)
В случае, если передаточная функция 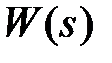 соответствует статической системе (соответствие астатической системе рассмотрим ниже), то при
соответствует статической системе (соответствие астатической системе рассмотрим ниже), то при 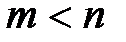 АФЧХ
АФЧХ 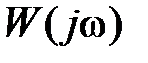 при изменении
при изменении 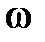 от
от 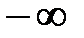 до
до 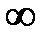 всегда образует замкнутую кривую. Соответственно
всегда образует замкнутую кривую. Соответственно 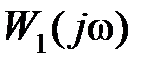 в комплексной плоскости также всегда образует замкнутую кривую. Таким образом, условие (5.13) для замкнутой кривой
в комплексной плоскости также всегда образует замкнутую кривую. Таким образом, условие (5.13) для замкнутой кривой 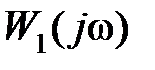 соответствует тому, что вектор
соответствует тому, что вектор 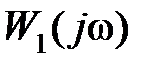 при изменении
при изменении 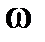 от
от 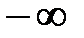 до
до 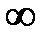 должен в положительном направлении обойти (охватить) начало координат
должен в положительном направлении обойти (охватить) начало координат
l раз. Из связи 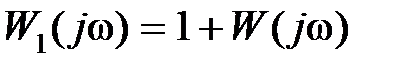 для АФЧХ
для АФЧХ 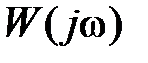 это соответствует охвату точки с координатами (–1, j0) на комплексной плоскости l раз годографом
это соответствует охвату точки с координатами (–1, j0) на комплексной плоскости l раз годографом 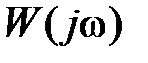 . На основании изложенного сформулируем критерий.
. На основании изложенного сформулируем критерий.
К p ит ep ий H айквиста. Если разомкнутая система автоматического управления имеет l правых корней, то для того, чтобы замкнутая система была устойчива, необходимо и достаточно, чтобы АФЧХ разомкнутой системы 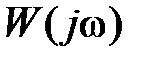 при изменении частоты
при изменении частоты 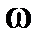 от
от 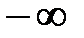 до
до 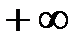 охватывала точку (–1, j0) на комплексной плоскости в положительном направлении l раз.
охватывала точку (–1, j0) на комплексной плоскости в положительном направлении l раз.
Частный случай критерия Найквиста относится к системе, устойчивой в разомкнутом состоянии (l = 0). При этом годограф 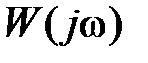 не должен охватывать точку (–1, j0).
не должен охватывать точку (–1, j0).
Так как при  график
график 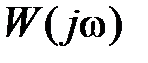 является зеркальным отображением относительно действительной оси графика при
является зеркальным отображением относительно действительной оси графика при  , то обычно достаточно построить
, то обычно достаточно построить 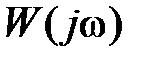 для
для  . При этом в формулировке критерия полагают охват точки (–1, j0)
. При этом в формулировке критерия полагают охват точки (–1, j0) 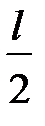 раз.
раз.
На рис. 5.4, а, б представлены графики 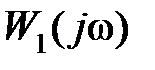 ,
, 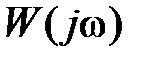 в предположении
в предположении
l = 2 для случая устойчивой в замкнутом состоянии системы.
Из изложенного следует, что при корректном применении критерия устойчивости Найквиста следует сначала исследовать устойчивость разомкнутой системы и знать число правых корней ее характеристического уравнения. На практике обычно это нетрудно сделать по виду передаточной функции 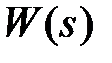 , если она представлена в виде произведения передаточных функций отдельных звеньев.
, если она представлена в виде произведения передаточных функций отдельных звеньев.
Рис. 5.4
В случае астатической системы формулировка критерия Найквиста сохраняется, однако при этом возникает проблема понятия охвата и неохвата точки (–1, j0), так как при 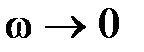 годограф
годограф 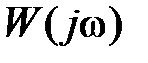 уходит в бесконечность и кривая
уходит в бесконечность и кривая 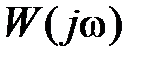 не является замкнутой. В этом случае АФЧХ дополняется дугой бесконечного радиуса по часовой стрелке и после этого проверяется выполнение условия критерия Найквиста. Изображенная на рис. 5.5 система устойчива.
не является замкнутой. В этом случае АФЧХ дополняется дугой бесконечного радиуса по часовой стрелке и после этого проверяется выполнение условия критерия Найквиста. Изображенная на рис. 5.5 система устойчива.
|
| Для нормального функционирования система управления должна обладать и некоторыми запасами устойчивости, т.е. при изменении параметров системы в процессе работы свойство устойчивости должно сохраняться.
Вполне очевидно, что чем дальше находится кривая 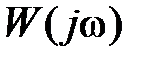 от точки от точки 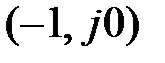 , тем система будет находиться дальше от границы устойчивости. Числовые величины, характеризующие это свойство, носят название запасов устойчивости и могут быть введены различными способами. , тем система будет находиться дальше от границы устойчивости. Числовые величины, характеризующие это свойство, носят название запасов устойчивости и могут быть введены различными способами.
|
На рис. 5.6 представлена АФЧХ разомкнутой системы для устойчивой замкнутой системы.
| | 3апас устойчивости по фаз e определяется как величина угла 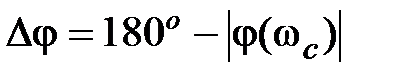 , где , где 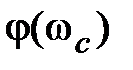 –значение фазы при –значение фазы при 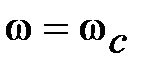 , а частота среза , а частота среза 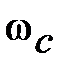 – это значение частоты, при которой – это значение частоты, при которой 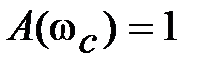 . Из рис. 5.6 видно, что точка В получается пересечением . Из рис. 5.6 видно, что точка В получается пересечением 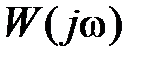 и окружности единичного радиуса (штриховая линия).
Запас устойчивости по амплитуде и окружности единичного радиуса (штриховая линия).
Запас устойчивости по амплитуде 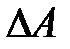 – это величина отрезка оси абсцисс между критической точкой – это величина отрезка оси абсцисс между критической точкой 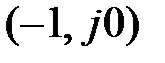 и точкой С пересечения и точкой С пересечения 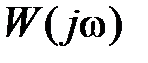 c осью абсцисс c осью абсцисс
|
(там, где 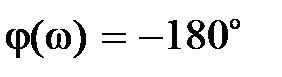 ). Очевидно, в данном случае величина
). Очевидно, в данном случае величина 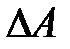 всегда меньше единицы.
всегда меньше единицы.
Если характеристика 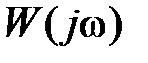 имеет более сложные очертания (так называемая клювообразная характеристика представлена на рис. 5.7), то запас по амплитуде характеризуют двумя числами
имеет более сложные очертания (так называемая клювообразная характеристика представлена на рис. 5.7), то запас по амплитуде характеризуют двумя числами 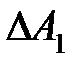 ,
, 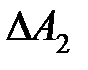 , а запас по фазе
, а запас по фазе 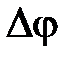 определяется обычным образом.
определяется обычным образом.
| | Рассмотрим интерпретацию критерия Найквиста в логарифмической области. Для простоты рассмотрим систему, устойчивую в paзoмкнутом состоянии, для которой АФЧХ разомкнутой системы 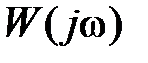 не должна охватывать точку (–1, j0). Очевидно, «опасным» с точки зрения устойчивости является отрезок действительной оси не должна охватывать точку (–1, j0). Очевидно, «опасным» с точки зрения устойчивости является отрезок действительной оси 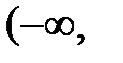 –1), когда фазовая характеристика равна –π, –3π и т.д. При –1), когда фазовая характеристика равна –π, –3π и т.д. При
|
этом модуль 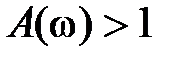 . Пересечение же отрезка действительной оси (–1, 0) годографом
. Пересечение же отрезка действительной оси (–1, 0) годографом 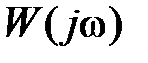 безопасно с точки зрения устойчивости. Если перейти к логарифмическим частотным характеристикам
безопасно с точки зрения устойчивости. Если перейти к логарифмическим частотным характеристикам 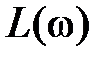 и
и 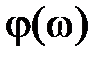 , то характеристики, приведенные на рис. 5.7, будут соответствовать логарифмическим характеристикам, изображенным на рис. 5.8.
, то характеристики, приведенные на рис. 5.7, будут соответствовать логарифмическим характеристикам, изображенным на рис. 5.8.
Рис. 5.8
В общем случае критерий Найквиста применительно к логарифмическим характеристикам формулируется так: для устойчивости замкнутой системы необходимо и достаточно, чтобы разность между числом положительных и отрицательных переходов логарифмической фазовой частотной характеристикой 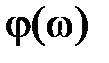 разомкнутой системы прямых
разомкнутой системы прямых 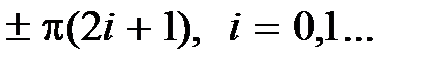 во всех областях,
во всех областях, 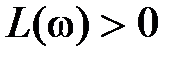 была равна
была равна 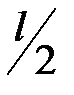 (l – число правых корней характеристического уравнения разомкнутой системы).
(l – число правых корней характеристического уравнения разомкнутой системы).
Отметим, что 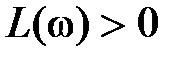 обычно до частоты среза системы
обычно до частоты среза системы 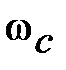 . Если система устойчива в разомкнутом состоянии, то l = 0.
. Если система устойчива в разомкнутом состоянии, то l = 0.
При использовании логарифмических характеристик также вводят запасы устойчивости, показанные на рис. 5.8. При 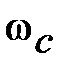 запас устойчивости по фазе определяется как
запас устойчивости по фазе определяется как 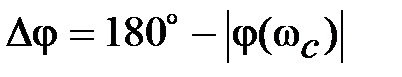 , а запас устойчивости по модулю характеризуется величинами отрезков
, а запас устойчивости по модулю характеризуется величинами отрезков 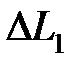 ,
, 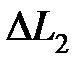 , выраженными в децибелах. В случае обычных, не клювообразных, характеристик
, выраженными в децибелах. В случае обычных, не клювообразных, характеристик 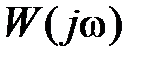 запас устойчивости по модулю характеризуется одной величиной
запас устойчивости по модулю характеризуется одной величиной 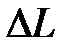 , определяемой на критической частоте
, определяемой на критической частоте 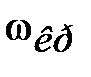 , соответствующей
, соответствующей 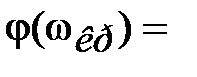 –180o.
–180o.
На практике величина запасов устойчивости по фазе и модулю обычно колеблется в пределах 30o…60o и (6…20) дБ. Величина (6...20) дБ соответствует усилению в (2...10) раз.
Рассмотрим, как в общих чертах влияют параметры и вид АФЧХ разомкнутой системы 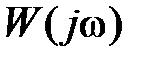 на устойчивость. Если
на устойчивость. Если 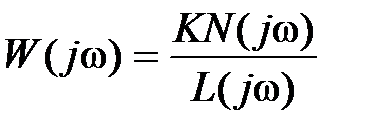 , то очевидно, что величина коэффициента усиления не влияет на вид фазовой частотной характеристики. Модуль
, то очевидно, что величина коэффициента усиления не влияет на вид фазовой частотной характеристики. Модуль 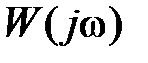 пропорционален величине K. Таким образом, увеличение (уменьшение) величины K будет пропорционально увеличивать (уменьшать)
пропорционален величине K. Таким образом, увеличение (уменьшение) величины K будет пропорционально увеличивать (уменьшать) 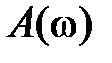 , не изменяя фазового угла годографа вектора
, не изменяя фазового угла годографа вектора 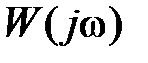 в комплексной плоскости. кривая
в комплексной плоскости. кривая 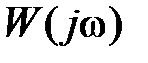 (см. рис. 5.6) будет пропорционально расширяться или сжиматься, и с увеличением K наступит момент, когда
(см. рис. 5.6) будет пропорционально расширяться или сжиматься, и с увеличением K наступит момент, когда 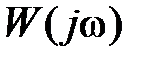 охватит точку (–1, j0) и система станет неустойчивой. Это следует и по ЛАЧХ (см. рис. 5.8). Увеличение K поднимает характеристику
охватит точку (–1, j0) и система станет неустойчивой. Это следует и по ЛАЧХ (см. рис. 5.8). Увеличение K поднимает характеристику 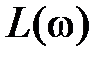 , приводит к смещению
, приводит к смещению 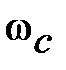 вправо по оси абсцисс и в конечном счете к потере устойчивости.
вправо по оси абсцисс и в конечном счете к потере устойчивости.
В случае клювообразных характеристик (см. рис. 5.7, 5.8) возможна потеря устойчивости и при уменьшении общего коэффициента усиления. Увеличение порядка астатизма системы также отрицательно сказывается на устойчивости, так как приводит к увеличению отрицательных фазовых сдвигов.
20. Понятие точности. Постоянные ошибки.
Обратимся к стандартной структуре системы автоматического управления, представленной на рис. 3.1. Основным назначением системы является как можно более точное воспроизведение управляющего сигнала. Естественно, что точность системы можно оценивать величиной разности управляющего сигнала 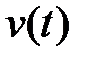 и выхода
и выхода 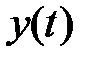 , т.е. величиной ошибки
, т.е. величиной ошибки 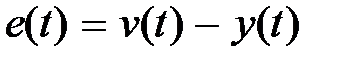 . Очевидно, чем меньше величина
. Очевидно, чем меньше величина 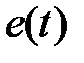 пo модулю в каждый данный момент времени, тем система с большей точностью (меньшей ошибкой) воспроизводит управляющий сигнал. На практике интересуются не полной ошибкой системы
пo модулю в каждый данный момент времени, тем система с большей точностью (меньшей ошибкой) воспроизводит управляющий сигнал. На практике интересуются не полной ошибкой системы 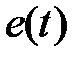 , а так называемой установившейся ошибкой
, а так называемой установившейся ошибкой 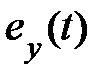 , которую определяют для достаточно больших моментов времени после затухания переходной составляющей.
, которую определяют для достаточно больших моментов времени после затухания переходной составляющей.
Изображение ошибки в соответствии с рис. 3.1 можно записать в виде
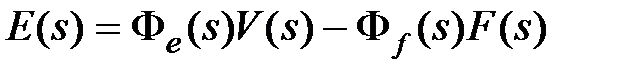 , (6.1)
, (6.1)
где 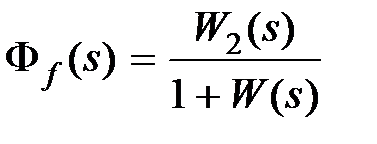 ,
, 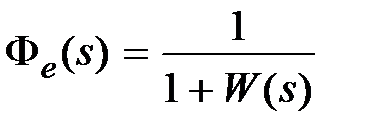 ,
, 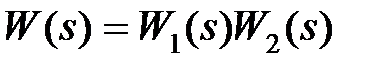 .
.
Из (6.1) следует, что ошибка системы будет определяться суммой двух составляющих: ошибкой системы от управляющего и ошибкой системы от возмущающего воздействий. В силу линейности системы методика вычисления каждой из этих составляющих будет однотипной, поэтому рассмотрим лишь методы вычисления ошибки системы от управляющего сигнала.
При определенных типах воздействий и определенной структуре системы установившаяся ошибка в системе будет постоянной и может быть вычислена на основании правил операционного исчисления по выражению
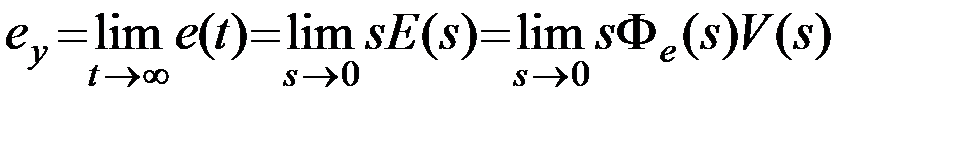 . (6.2)
. (6.2)
Рассмотрим входные воздействия: 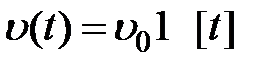 ,
, 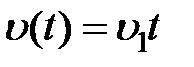 ,
, 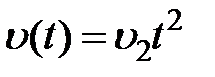 ,
, 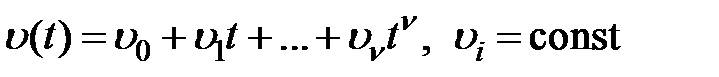 , изображения которых будут соответственно равны:
, изображения которых будут соответственно равны: 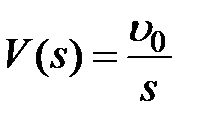 ,
, 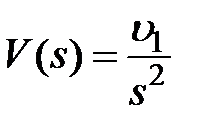 ,
, 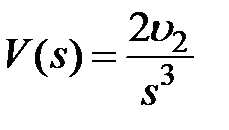 ,
, 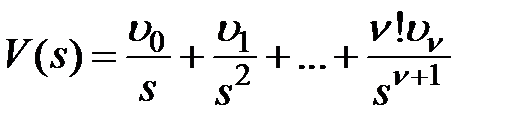 .
.
Пусть передаточная функция разомкнутой системы 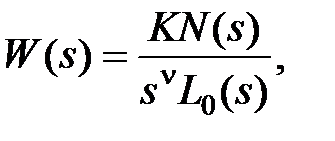
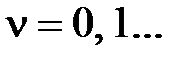 .
.
Если 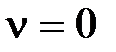 (статическая система),
(статическая система), 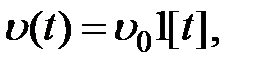 то, подставляя в (6.2)
то, подставляя в (6.2) 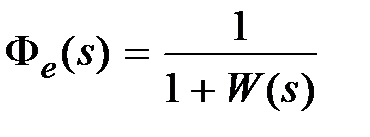 и
и 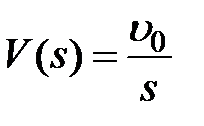 , получим
, получим
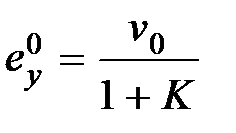 . (6.3)
. (6.3)








