Отметим некоторые общие свойства частотных характеристик для систем минимально-фазового типа. Пусть и степень полинома числителя m меньше степени полинома знаменателя n, тогда
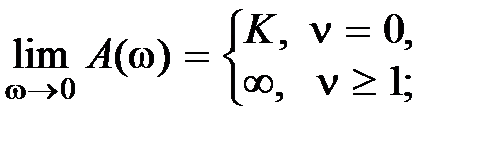
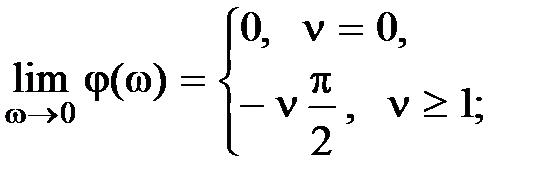
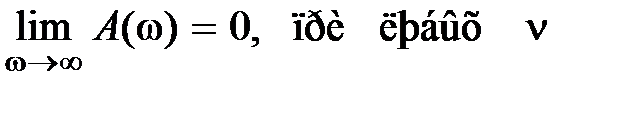 ;
; 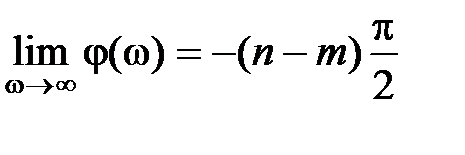 .
.
При этом годограф 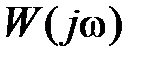 на комплексной плоскости при
на комплексной плоскости при 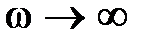 стремится к началу координат, при
стремится к началу координат, при 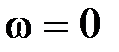 для статической системы он начинается на действительной оси на расстоянии K от начала координат, а для астатических систем при
для статической системы он начинается на действительной оси на расстоянии K от начала координат, а для астатических систем при 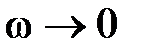 уходит в бесконечность в третьем квадранте при
уходит в бесконечность в третьем квадранте при 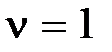 , во втором квадранте при
, во втором квадранте при 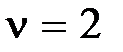 , в первом квадранте при
, в первом квадранте при 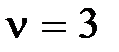 и т.д. по часовой стрелке.
и т.д. по часовой стрелке.
При построении частотных характеристик разомкнутой системы полезно представить W(s) в виде произведения передаточных функций 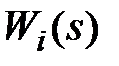 элементарных звеньев (см. подразд. 2.5), т.e.
элементарных звеньев (см. подразд. 2.5), т.e. 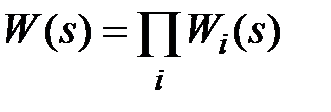 . В этом случае
. В этом случае 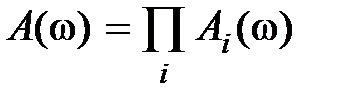 ,
, 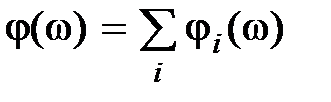 ,
, 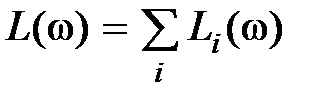 , что может существенно облегчить вычисление и построение характеристик. Если
, что может существенно облегчить вычисление и построение характеристик. Если 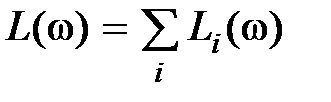 , то каждую элементарную характеристику
, то каждую элементарную характеристику 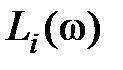 строят в виде отрезков ломаных (асимптот) и далее производят суммирование. Отметим, что первая низкочастотная асимптота определяется выражением
строят в виде отрезков ломаных (асимптот) и далее производят суммирование. Отметим, что первая низкочастотная асимптота определяется выражением 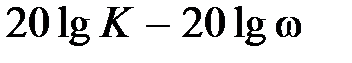 – это есть прямая с наклоном (
– это есть прямая с наклоном ( 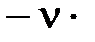 20 дБ/дек), проходящая при
20 дБ/дек), проходящая при 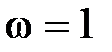 через точку с координатой
через точку с координатой 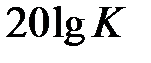 .
.
Рассмотрим теперь частотные характеристики замкнутой системы. Их можно получить по передаточным функциям замкнутой системы 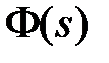 ,
, 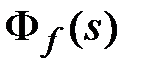 ,
, 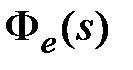 . Чаще всего рассматривают частотные характеристики на базе главной передаточной функции замкнутой системы
. Чаще всего рассматривают частотные характеристики на базе главной передаточной функции замкнутой системы 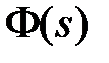 . Из них обычно используются
. Из них обычно используются 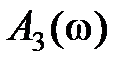 =
= 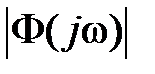 – АЧХ и
– АЧХ и 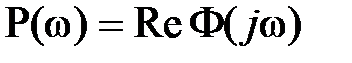 – вещественная частотная характеристика замкнутой системы.
– вещественная частотная характеристика замкнутой системы.
Остановимся на основных свойствах 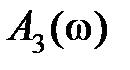 и
и 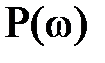 . Для физически реализуемых систем
. Для физически реализуемых систем 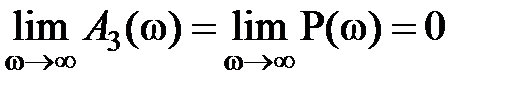 . Начальные значения этих характеристик будут
. Начальные значения этих характеристик будут

Между частотными характеристиками разомкнутой и замкнутой системы существует однозначная связь, которая следует из выражения
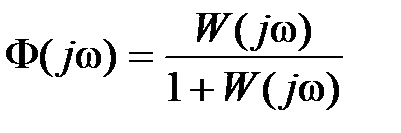 . (3.7)
. (3.7)
Представляя 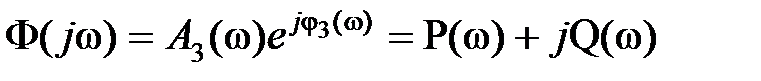 и
и 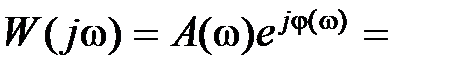
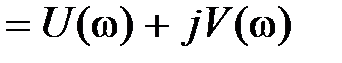 , из (3.7) можно получить следующие выражения:
, из (3.7) можно получить следующие выражения:
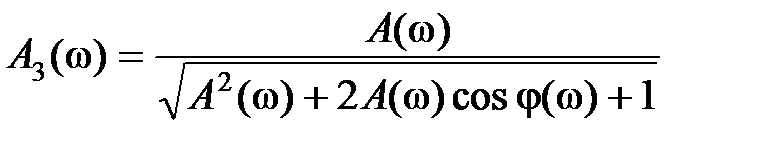 ,
, 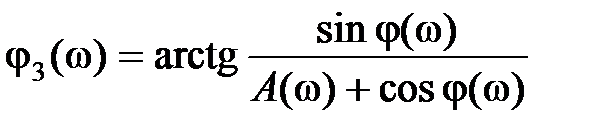 ,
,
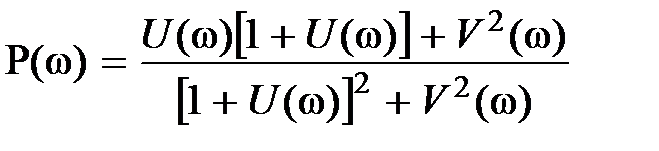 ,
, 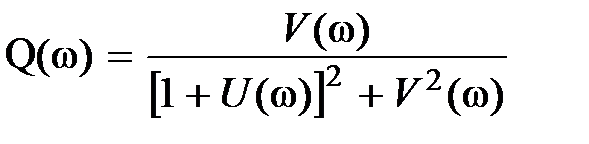 ,
,
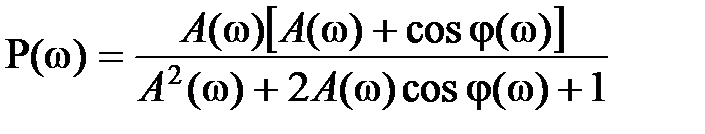 ,
, 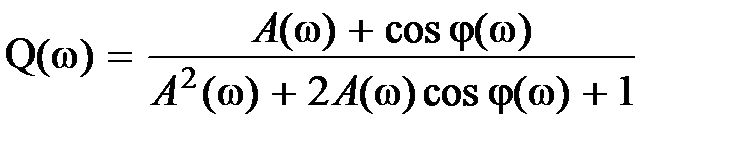 .
.
Эти выражения можно использовать для вычисления частотных характеристик замкнутой системы по частотным характеристикам разомкнутой. Существуют специальные номограммы, решающие такие задачи графически.
15. Общие описания процессов.
Динамические процессы в стандартной системе автоматического управления, структурная схема которой приведена на рис. 3.1, описываются во временной области дифференциальным уравнением
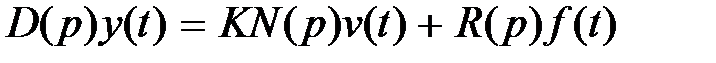 (4.1)
(4.1)
или в области изображений выражением
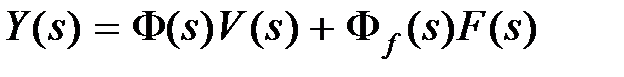 . (4.2)
. (4.2)
Выходной сигнал y(t) замкнутой системы, являющийся решением линейного дифференциального уравнения (4.1), может возникнуть в системе либо за счет внешних воздействий v(t) или f(t), либо за счет вариации начальных условий переменной y(t) и ее производных. Составляющую выходного сигнала, обусловленную ненулевыми начальными условиями переменной y(t) и ее производных, будем называть свободной и обозначать y С(t), а составляющие, обусловленные сигналами v(t) и f(t), – вынужденными и обозначать соответственно y v в(t) и yf в(t). Тогда процесс y(t), являющийся решением линейного дифференциального уравнения (4.1), определяется выражением
y(t) = y С (t) + y в(t) = y С (t) + y v в(t) + yf в(t), (4.3)
где y в(t) = y v в(t) + yf в(t).
В математике y С (t) называют общим решением уравнения (4.1) без правой части (однородного уравнения), a y в(t) – частным решением уравнения (4.1) с правой частью (неоднородного уравнения).
Общее решение однородного уравнения в случае простых (различных) корней характеристического уравнения 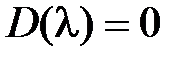 , которые обозначим через
, которые обозначим через 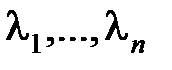 , определяется выражением
, определяется выражением
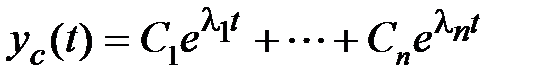 , (4.4)
, (4.4)
где С i – произвольные постоянные, определяемые через начальные условия 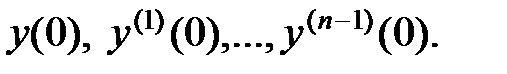
Если характеристическое уравнение 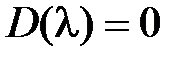 имеет один кратный корень, например
имеет один кратный корень, например 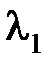 кратности r, а остальные
кратности r, а остальные 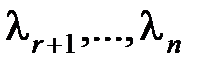 – простые, то общее решение будет иметь вид
– простые, то общее решение будет иметь вид
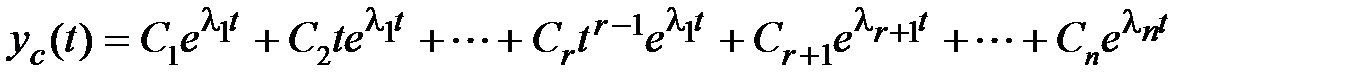 . (4.5)
. (4.5)
В случае нескольких кратных корней в свободной составляющей будут появляться аналогичные группы слагаемых, соответствующие каждому кратному корню.
Для вычисления вынужденной составляющей обратимся к уравнению
относительно изображений (4.2). Обозначим весовые функции замкнутой системы по управляющему сигналу 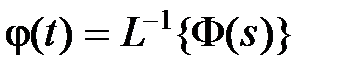 и по возмущению
и по возмущению 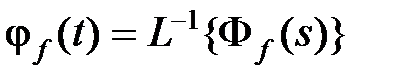 , тогда переходя в (4.2) к оригиналам, с учетом того, что произведение изображений есть свертка во временной области, получим
, тогда переходя в (4.2) к оригиналам, с учетом того, что произведение изображений есть свертка во временной области, получим
y в(t) = y v в(t) + y f в(t) 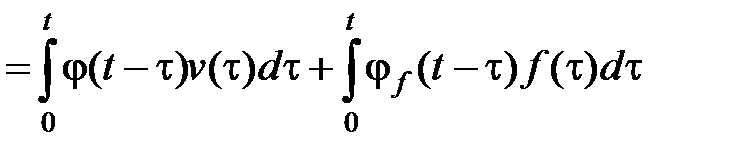 . (4.6)
. (4.6)
Таким образом, полное решение 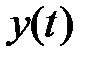 дифференциального уравнения будет иметь вид
дифференциального уравнения будет иметь вид
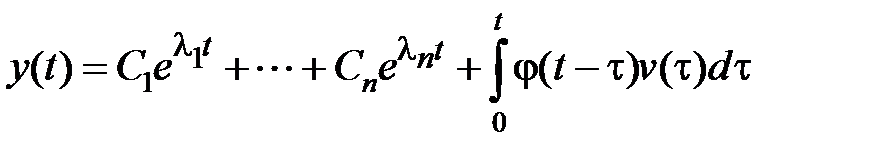
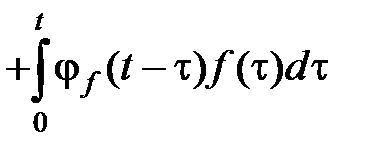 . (4.7)
. (4.7)
В случае нулевых начальных условий ( 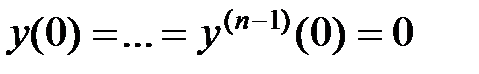 ) все
) все 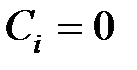 и (4.7) превращается в соотношение (4.6).
и (4.7) превращается в соотношение (4.6).
При исследовании систем управления обычно ограничиваются внешними воздействиями определенного типа, что дает возможность ввести некоторые показатели качества процессов управления и оказывается удобным для сравнительного анализа проектируемых систем. Наиболее часто сигнал уп равления v(t) (то же самое и для возмущения 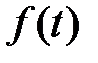 ) задают в виде типового сигнала следующего вида:
) задают в виде типового сигнала следующего вида:
v(t) = 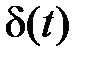 – дельта-функция;
– дельта-функция;
v(t) = v01[t] – ступенчатая функция амплитуды v0 (скачок по положению);
v(t) = v1t – скачок по скорости;
v(t) = v2t2 – скачок по ускорению;
v(t) = v0+v1t + v2t2 +…+ v k tk – полиномиальное воздействие;
v(t) 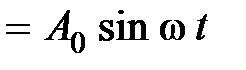 – гармоническое воздействие, где А0 амплитуда,
– гармоническое воздействие, где А0 амплитуда, 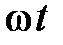 – фаза,
– фаза, 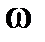 – частота;
– частота;
v(t) 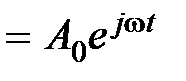 – гармоническое воздействие в комплексной форме.
– гармоническое воздействие в комплексной форме.
В этих выражениях сигналы определены при t > 0 и paвны нулю при 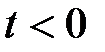 , a v i = const, A0 = const,
, a v i = const, A0 = const, 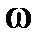 = const.
= const.
Выбор того или иного сигнала зависит от вида системы и условий ее функционирования. Например, для систем стабилизации наиболее естественной формой управляющего воздействия является ступенчатая функция. Для следящих систем таковыми являются сигналы гармонического типа.
Наиболее часто динамические свойства системы оцениваются по ее реакции на единичную ступенчатую функцию v(t) = 1[t], т.е. по виду выходного сигнала 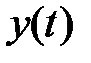 , являющегося переходной функцией замкнутой системы h з (t).
, являющегося переходной функцией замкнутой системы h з (t).
На рис. 4.1 представлен наиболее типичный вид переходной функции h з (t), где 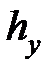 – установившееся значение выходной координаты.
– установившееся значение выходной координаты.
| | Для оценки качества регулирования по виду h з(t) вводят показатели качества:
t р – время регулирования (время переходного процесса), это время, после которого величина 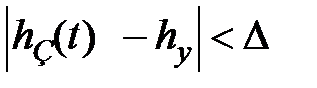 , где обычно ∆ = 5 % от h y; , где обычно ∆ = 5 % от h y;
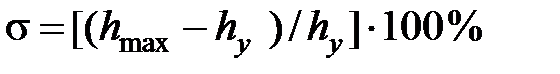 – перерегулирование в процентах; – перерегулирование в процентах;
|
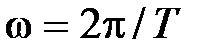 – частота колебаний переходного процесса;
– частота колебаний переходного процесса;
число колебаний за время переходного процесса.
Наиболее важными показателями качества являются t р и  . Величина t р может изменяться в широких пределах в зависимости от вида системы управления. Перерегулирование обычно лежит в пределах от 0 до 30 %. Число колебаний за время регулирования обычно 1–2, а иногда 3–4. В некоторых случаях колебания недопустимы.
. Величина t р может изменяться в широких пределах в зависимости от вида системы управления. Перерегулирование обычно лежит в пределах от 0 до 30 %. Число колебаний за время регулирования обычно 1–2, а иногда 3–4. В некоторых случаях колебания недопустимы.
По виду функции h з(t) процессы делятся на три категории (рис. 4.2):
монотонные (1), апериодические (2) и колебательные (3).
| | У монотонных процессов 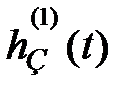 не меняет знак, у апериодического процесса знак производной не меняет знак, у апериодического процесса знак производной 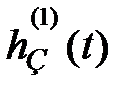 изменяется только один раз, у колебательного – бесконечное число раз.
Вычисление процессов в замкнутой системе фактически представляет собой задачу решения дифференциального уравнения (4.1) при заданных входных воздействиях v(t) и f(t) и начальных усло- изменяется только один раз, у колебательного – бесконечное число раз.
Вычисление процессов в замкнутой системе фактически представляет собой задачу решения дифференциального уравнения (4.1) при заданных входных воздействиях v(t) и f(t) и начальных усло-
|
виях. Существующие методы решения этой задачи можно разбить на две категории: аналитические методы и методы моделирования на ПЭВМ.
16. Понятие устойчивости линейных систем.
Общие определения устойчивости процессов, справедливые как для линейных, так и для нелинейных систем, будут даны во второй части конспекта лекций. Здесь отметим, что свойство устойчивости или неустойчивости заданного процесса, протекающего в системе, рассматривается по отношению к другим процессам той же системы, отличающимся от заданного за счет изменений начальных условий. величинами, отклоняющими процесс от заданного, являются возмущения начальных условий.
Для случая линейной системы динамические процессы в ней описываются линейным дифференциальным уравнением:
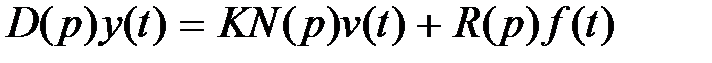 , (5.1)
, (5.1)
общее решение которого определяется выражением (4.3): 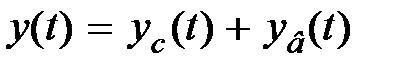 .
.
Изменение начальных условий влияет только на поведение свободной составляющей и не влияет на 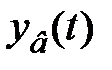 , откуда следует, что устойчивость будет определяться поведением свободной составляющей. Если
, откуда следует, что устойчивость будет определяться поведением свободной составляющей. Если 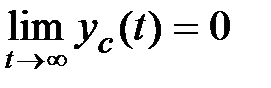 , тo процессы в линейной системе будем называть асимптотич eски устойчивыми, при
, тo процессы в линейной системе будем называть асимптотич eски устойчивыми, при 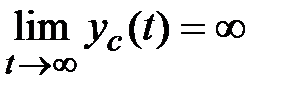 – н eустойчивыми, и если при любом
– н eустойчивыми, и если при любом 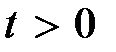 свободная составляющая ограничена, то процессы будут просто устойчивы. Если одно из указанных свойств присуще какому-либо процессу, то для линейной системы оно будет справедливо для всех процессов. Поэтому принято говорить об асимптотической устойчивости, неустойчивости или просто устойчивости линейной системы. В последнем случае еще говорят, что линейная система находится на границе устойчивости или является н eйт pальной.
свободная составляющая ограничена, то процессы будут просто устойчивы. Если одно из указанных свойств присуще какому-либо процессу, то для линейной системы оно будет справедливо для всех процессов. Поэтому принято говорить об асимптотической устойчивости, неустойчивости или просто устойчивости линейной системы. В последнем случае еще говорят, что линейная система находится на границе устойчивости или является н eйт pальной.
Структура свободной составляющей имеет вид (4.4) или (4.5).
Из (4.4), (4.5) следует, что поведение свободной составляющей во времени не зависит от величин 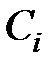 и соответственно от начальных условий, а полностью определяется видом корней
и соответственно от начальных условий, а полностью определяется видом корней 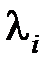 .
.








