Частные случаи колебательного звена: конс ep вативно e зв e но при , имеющее передаточную функцию , и апериодическое звено второго по p ядка при , передаточная функция которого равна
, 
.
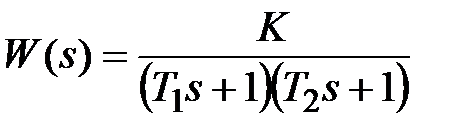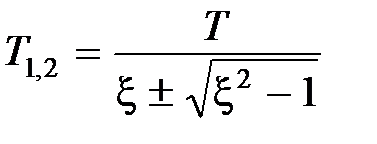10. Элементарные звенья: форсующее звено первого порядка.
Фо p си p ующе e зв e но п ep вого по p ядка. Дифференциальное уравнение и передаточная функция звена имеют вид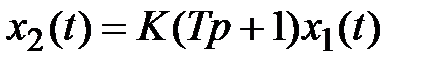 
, 
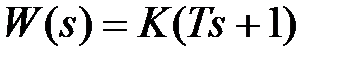, а частотные и временные характеристики определяются выражениями
, 
, 
, 
, 
, 
.
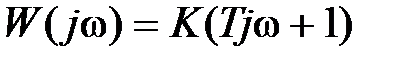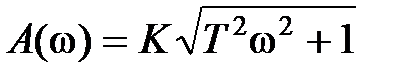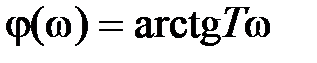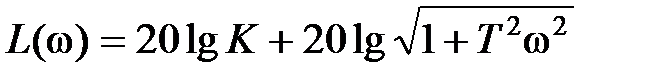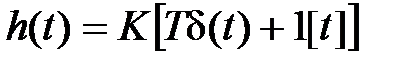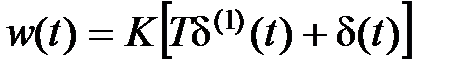Графики частотных характеристик представлены на рис. 2.14.
Рис. 2.14
Фо p си p ующ e е зв e но второго по p ядка. Диффференциальное уравнение и передаточная функция равны соответственно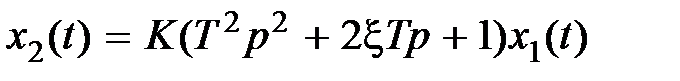 
, 
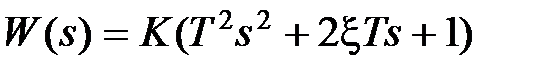при условии 
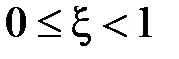. При 
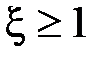это звено можно представить как произведение двух элементарных форсирующих звеньев первого порядка.
11. Особенности и физическая реализация звеньев.
Пусть звено имеет передаточную функцию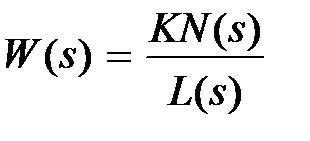 
.
Если нули передаточной функции (корни уравнения N(s) = 0) и полюса передаточной функции (корни уравнения L(s) = 0) имеют действительные части, отрицательные или равные нулю, то такое звено будем называть звеном минимально-фазового типа. При наличии хотя бы одного нуля или полюса с положительной вещественной частью звено будет относиться к н e минимально-фазовому типу.
Рассмотрим эти звенья на простейшем примере. Для звена с передаточной функцией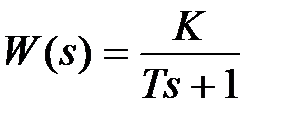 
, которое является минимально-фазовым, 
, 
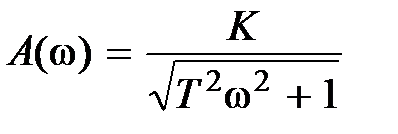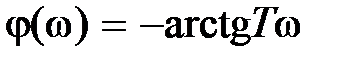. Звено с передаточной функцией 
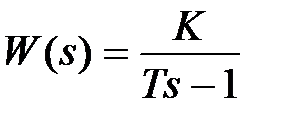, являющееся неминимально-фазовым, имеет частотные характеристики 
, 
.
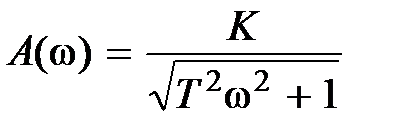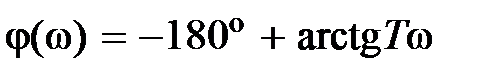Таким образом, при одинаковых АЧХ неминимально-фазовое звено имеет больший по модулю фазовый сдвиг.
Указанное свойство справедливо и в общем случае.
Рассмотрим еще одно важное свойство звеньев – свойство физической реализуемости.
Для любого реального устройства АЧХ с увеличением частоты должна уменьшаться и стремиться к нулю, а фазовые сдвиги на высоких частотах должны быть отрицательными. Пусть полином числителя К N(s) передаточной функции W(s) имеет порядок m, а полином знаменателя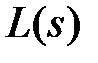 
– порядок 
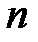. Тогда для минимально-фазового звена справедливы следующие соотношения:
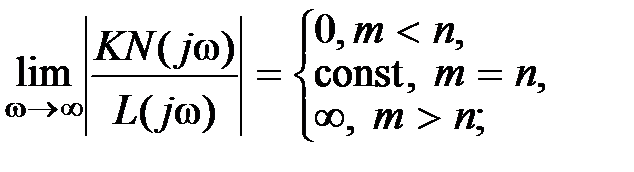
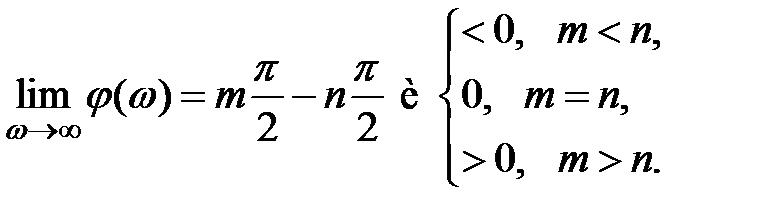
Из приведенных соотношений следует, что звено является физически реализуемым, если будет выполняться соотношение 
.
С этой точки зрения, например, идеальное дифференцирующее звено с передаточной функцией W(s) = Ks не является физически реализуемым. Реальное звено, осуществляющее операции дифференцирования, может быть аппроксимировано передаточной функцией W(s) = Ks в некотором ограниченном диапазоне частот.
12. Структурные схемы и структурные преобразования.
Графически системы автоматического управления представляют в
виде ст pукту pны x с xeм, которые разделяют на конструктивные, функциональные и алгоритмические. В случае конструктивных схем блок является
законченным техническим устройством (двигатель, усилитель, тахогенератор
и т.п.). В функциональных схемах блок представляет собой один или несколько элементов, осуществляющих какую-либо функцию (усиления, преобразования, сбора информации и т.п.). Часто конструктивные блоки могут совпадать с
функциональными.
При математическом описании систем управления распространение получили алго pитмич eски e ст pукту pны e с xeмы, составной частью которых являются звенья систем. Характеристикой звена является его математическое описание в виде дифференциального уравнения, передаточной функции или другой характеристики. Наиболее часто такой характеристикой является передаточная функция, которая записывается внутри прямоугольника, изображающего звено на структурной схеме.
Таким образом, алгоритмические структурные схемы, которые в основном
в дальнейшем будем использовать и называть просто структурными схемами, являются графической интерпретацией математической модели системы
управления.
В процессе исследования структурные схемы подвергаются преобразованию: некоторые звенья могут объединяться в одно звено, другие, наоборот, подвергаются расчленению. Такие преобразования носят название ст pукту pны x п peоб pазований, которые фактически соответствуют преобразованиям математических моделей. В результате таких преобразований конечная структурная схема может сильно отличаться от исходной, а тем более от функциональной или конструктивной схемы.
Одним из результирующих итогов структурных преобразований является приведение произвольной структуры системы к некоторому стандартному виду. Структурная схема такой станд apтной сист eмы автоматического управления представлена на рис. 3.1, где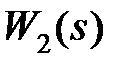 
– передаточная функция объекта управления, 
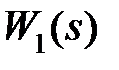– передаточная функция регулятора, v – входной сигнал, f – возмущающий, y – выходной сигнал, е – сигнал рассогласования. Единичная обратная связь в такой системе называется главной обратной связью.
| v |
Рис. 3.1
На структурных схемах сигналы следует рассматривать как изображения по Лапласу соответствующих переменных.
Рассмотрим преобразование произвольной структуры к стандартному виду, которое осуществляется на основании правил структурных преобразований. Анализ структур систем автоматического управления показывает, что существует три основных вида соединения звеньев: последовательное, па pa ллельно e и со e динени e с помощью обратной связи.
Структурные схемы, соответствующие указанным типам соединений, представлены на рис. 3.2, a, б, в.
Рис. 3.2
Отметим, что в дальнейшем, если это ясно из контекста, символ s в записи передаточных функций будем иногда опускать.
Рассмотрим задачу объединения звеньев в одно звено, связывающее непосредственно вход и выход соответствующего соединения.
Для последовательного соединения (см. рис. 3.2, а) можно записать: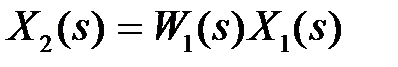 
, 
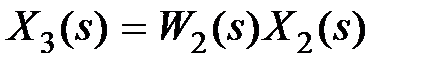. Исключая промежуточную величину 
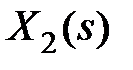, получим 
, 
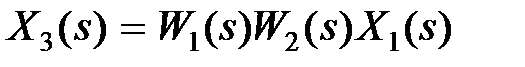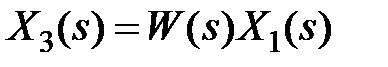. Итак, при последовательном соединении общая передаточная функция соединения будет равна произведению передаточных функций звеньев: 
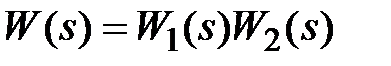. Если последовательно соединено i звеньев, то аналогично 
.
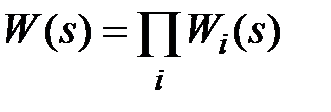Для параллельного соединения (см. рис. 3.2, б) уравнения, связывающие координаты, имеют вид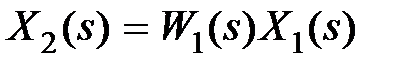 
, 
, 
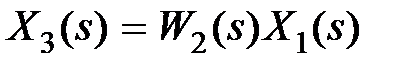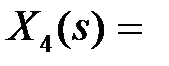
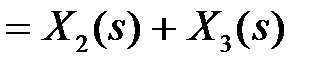. Исключая величины 
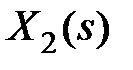и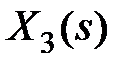 
из этих уравнений, получим 
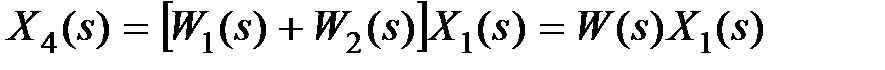, т.е. общая передаточная функция соединения будет равна сумме передаточных функций звеньев. В случае последовательного соединения i звеньев получим 
.
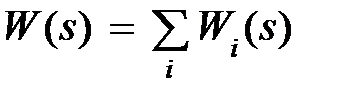Уравнения, связывающие переменные при соединении звеньев с помощью обратной связи (см. рис. 3.2, в), имеют вид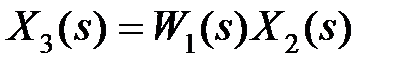 
, 
, 
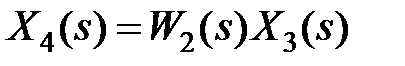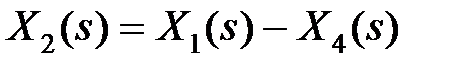, откуда, исключая переменные 
, 
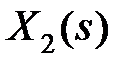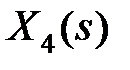, получим 
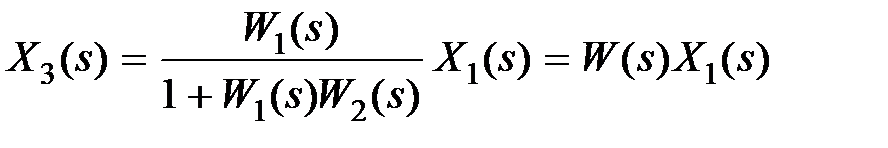, т.е. общая передаточная функция соединения будет равна 
.
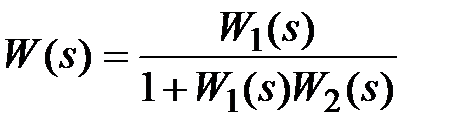Если звенья соединены с помощью положительной обратной связи, то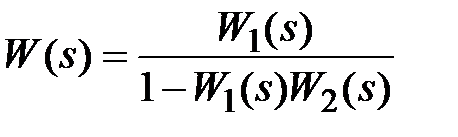 
.
Наряду с объединением звеньев при структурных преобразованиях приходится прибегать к переносу отдельных узлов или сумматоров из одних участков структурной схемы в другие. Такие переносы изображены на рис. 3.3,
где слева – исходная схема, а справа – структурная схема после соответствующего переноса узла или сумматора. Нетрудно видеть, что по отношению
к сигналам входа и выхода исходная и преобразованная структурные схемы эквивалентны.
Рис. 3.3
На практике существует и другая задача – расчленения отдельного звена на более простые. Примером решения такой задачи может служить представление передаточной функции звена в виде суммы или произведения передаточных функций элементарных звеньев.
13. Передаточные функции и уравнения систем.
Рассмотрим структурную схему стандартной системы автоматического управления, представленную на рис. 3.1. Обозначим произведение передаточных функций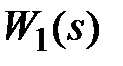 
, 
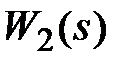через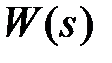 
. Эту передаточную функцию будем называть п epe даточной функци e й p азомкнутой сист e мы, которая связывает изображение выходного сигнала Y(s) и входа V(s) при размыкании цепи главной обратной связи и при f = 0.
Передаточная функция (как любая передаточная функция линейной системы или звена) есть отношение двух полиномов вида
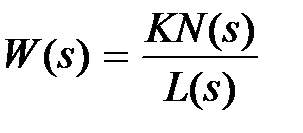, (3.1)
где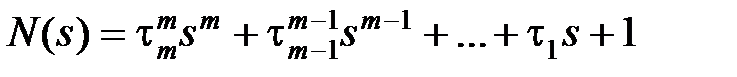 
, 
.
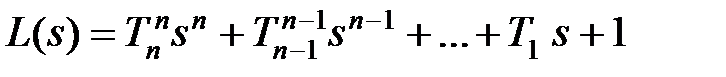Для физически реализуемых систем должно выполняться условие: m < n. Величину K будем называть коэффици e нтом п epe дачи (усил e ния) разомкнутой системы. Полином L(s) назовем xap акт ep истич e ским п o линомом разомкнутой системы, а алгебраическое уравнение n-й степени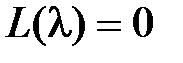 
, где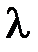 
– комплексная переменная, будем называть x аракт ep истич e ским у p авн e ни e м разомкнутой системы.