Ид e ально e инт e г p и p ующ ee зв e но. Дифференциальное уравнение и передаточная функция имеют вид , , .
Характеристики звена определяются следующими выражениями: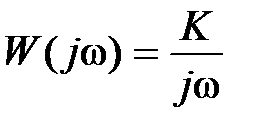 
, 
, 
, 
, 
, 
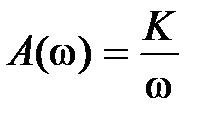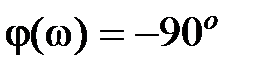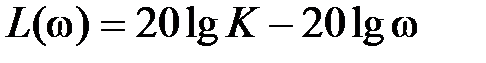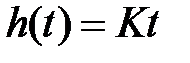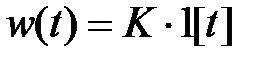, графики которых, за исключением последней, представлены на рис. 2.7.
рис. 2.7
7. Элементарные звенья: идеальное дифференцирующее звено.
Ид e ально e дифференцирующее e зв e но. Звено имеет следующие дифференциальное уравнение и передаточную функцию: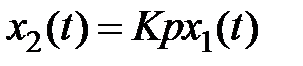 
, 
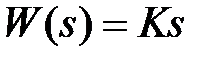и соответственно характеристики: 
, 
, 
, 
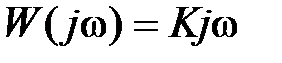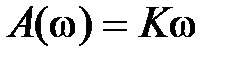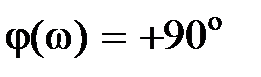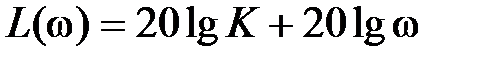, графики которых представлены на рис. 2.8. Временные характеристики определяются выражениями 
, 
.
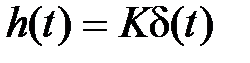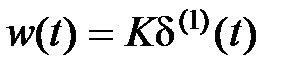Рис. 2.8
8. Элементарные звенья: апериодическое звено первого порядка.
A п ep иодич e ско e (ин ep ционно e ) зв e но п ep вого по p ядка. Дифференциальное уравнение звена имеет вид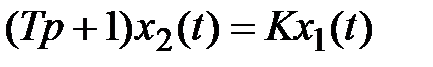 
.
Передаточная функция и частотные характеристики имеют вид
, 
, 
,
, 
.
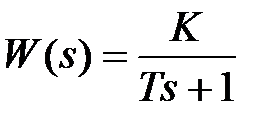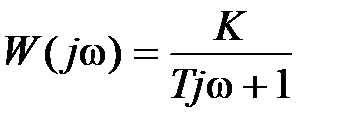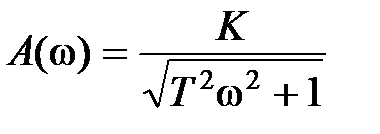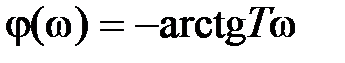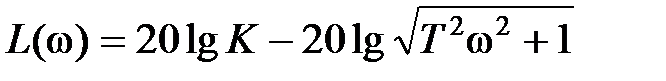Весовая и переходная функции звена определяются выражениями
, 
,
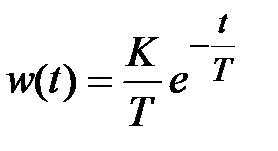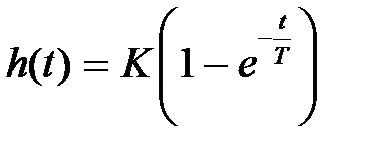графики которых представлены на рис. 2.9.
Рис. 2.9
На рис. 2.10 изображены частотные характеристики звена W(jω), A(ω),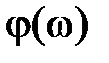 
. При этом годограф вектора 
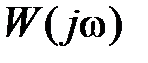представляет собой полуокружность.
рис. 2.10
ЛАЧХ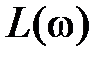 
может быть построена по приведенному выше выражению по точкам. Однако возможен более простой способ построения приближенной или асимптотической ЛАЧХ в виде отрезков прямых линий с наклонами: 0 до частоты 
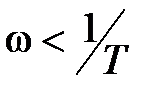и –20 дБ на декаду после частоты 
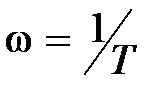. Соответствующий график приближенной (асимптотической) ЛАЧХ приведен на рис. 2.11, там же представлена и ЛФЧХ.
Рис. 2.11
Штриховой линией показан точный график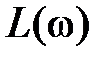 
. Максимальная ошибка 
между точным графиком 
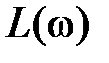и асимптотическим будет при 
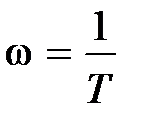и составит
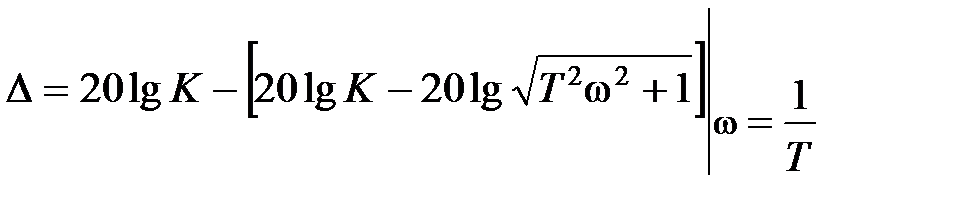
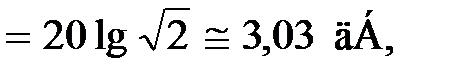
что вполне допустимо.
9. Элементарные звенья: колебательное звено.
Кол e бат e льно e зв e но. Дифференциальное уравнение колебательного эвена имеет вид
.
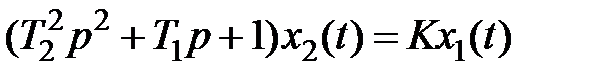Будем полагать, что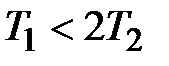 
, тогда корни характеристического уравнения 
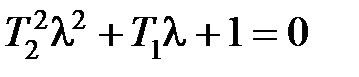будут комплексными. Чаще передаточную функцию звена записывают в ви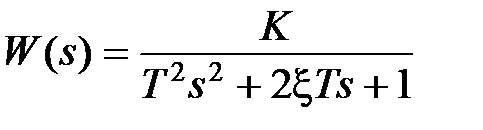де 
, где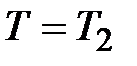 
, 
, 
.
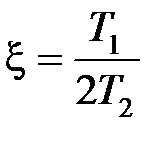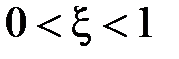Частотные и временные характеристики звена имеют следующий вид:
; 
;
,
, 
,
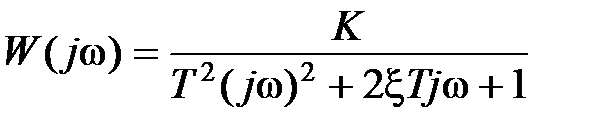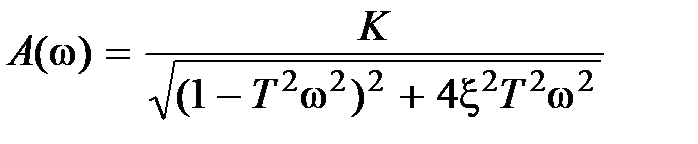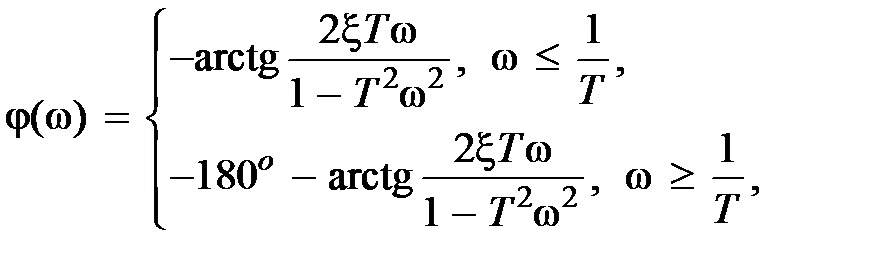
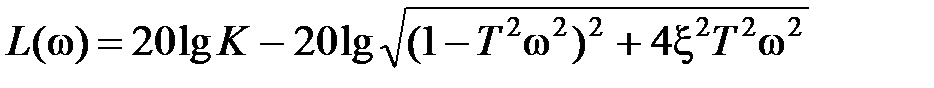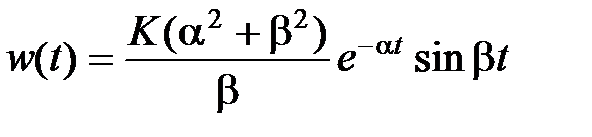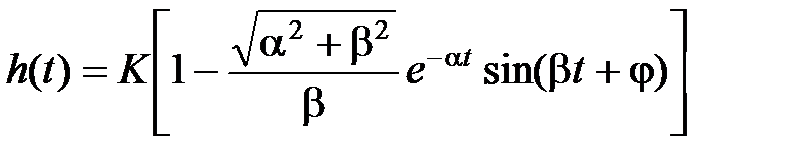где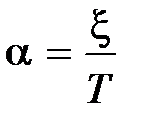 
, 
, 
.
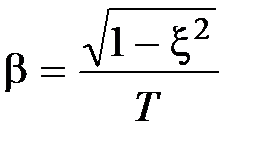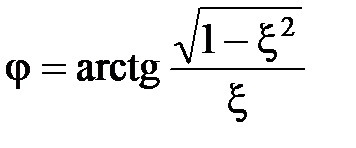Анализ АЧХ показывает, что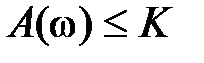 
для любого 
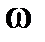, если 
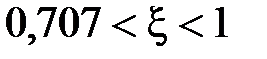. При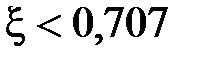 
на графике 
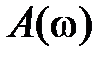появляется «горб», который уходит в бесконечность при 
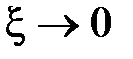. Величину 
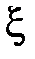называют параметром затухания. Чем меньше 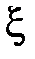, тем медленнее затухает колебательная составляющая в выражениях w(t) и h(t).
Асимптотическая ЛАЧХ в виде ломаной может быть получена только при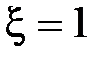 
и имеет следующий вид: 
.
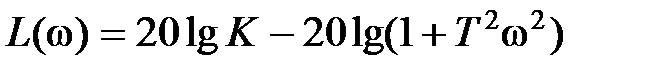Переход от прямой с наклоном 0 дБ/дек на прямую с наклоном –40 дБ/дек происходит на частоте излома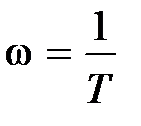 
. Считается, что такую аппроксимацию можно использовать 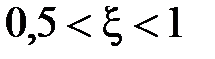при 
. При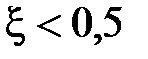 
в окрестностях точки 
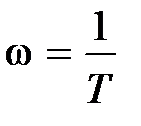на ЛАЧХ также появляется «гopб». В этом случае при построении 
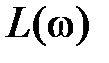в диапазоне 
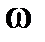, близких к 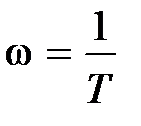, следует использовать точное выражение для 
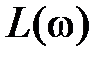или воспользоваться специальными номограммами.
Графики частотных характеристик колебательного звена приведены на рис. 2.12, а временных характеристик – на рис. 2.13.
рис. 2.12
рис. 2.13