П epe даточная функция звена W(s) есть отношение изображения выходного сигнала к изображению входного сигнала при нулевых начальных условиях.
Если взять дифференциальное уравнение звена в операторной форме (2.3), то формально W(s) получим делением оператора B(p) на оператор A(p) с заменой p на s: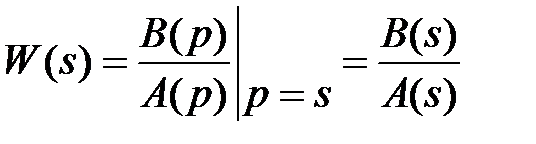 
.
Из (2.7) следует связь изображений входа и выхода через передаточную функцию:
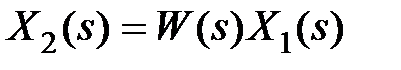. (2.8)
Звено САУ на структурных схемах изображают так, как показано на рис. 2.3.
| | При использовании уравнения (2.2) передаточную функцию звена будем записывать в виде |
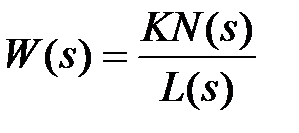, (2.9)
где N(s) и L(s) – многочлены с единичными коэффициентами в младших
членах.
Полином L(s) будем называть xap акт ep истич ec ким полиномом, а уравнение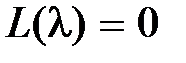 
– характеристическим уравнением звена.
Следующий класс характеристик звена – это временные характеристики: весовая и переходная функции звена.
Если рассматривать W(s) как изображение, то приходим к понятию весовой (импульсной) функции звeнa w(t), формально определяемой как обратное преобразование Лапласа от передаточной функции
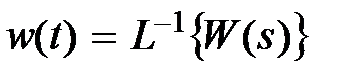. (2.10)
В e совая функция звена w(t) ecть реакция звена на входной сигнал в виде дельта-функции, которая определяется соотношением
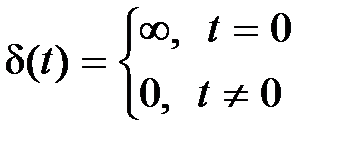, причем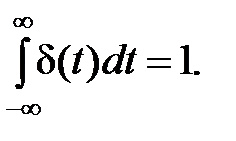 
Дельта-функция обладает фильтрующим свойством: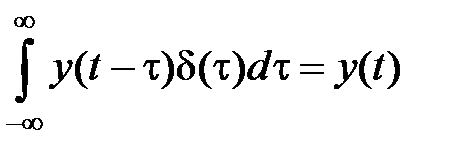 
.
Если положить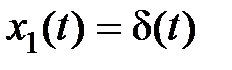 
, то 
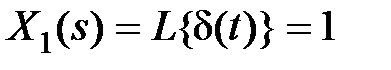и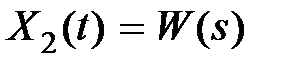 
, откуда 
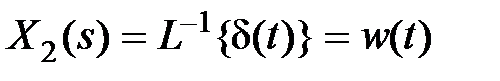, т.е. 
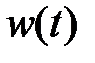– реакция звена на входной сигнал 
.
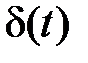К такому же результату можно прийти следующим образом. Правой части (2.8) соответствует в области оригиналов свертка функци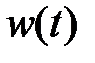й и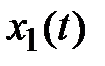 
:
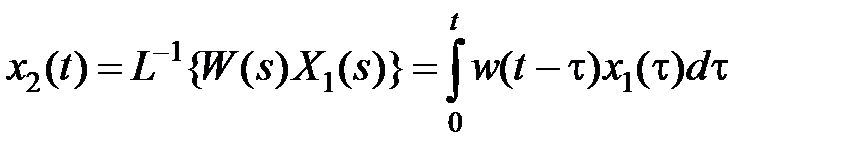. (2.11)
Если в (2.11) положить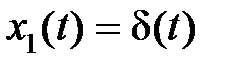 
, то на основании фильтрующего свойства дельта-функции будем иметь 
.
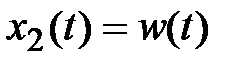П epex одной функци e й звена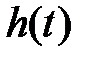 
называется реакция звена на единичное ступенчатое воздействие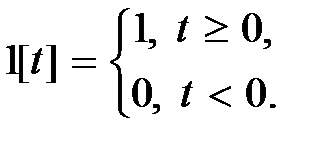 
Так как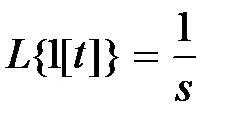 
, то 
и по определению
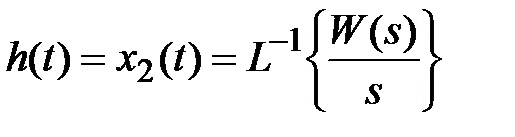. (2.12)
Так как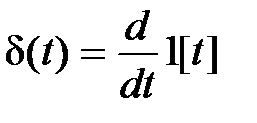 
, тo 
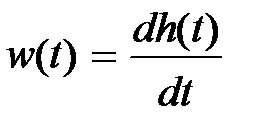, а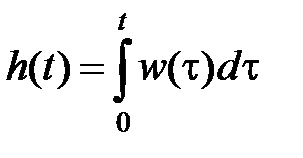 
.
5. Частотные характеристики звеньев.
Частотные характеристики определяют динамические свойства звеньев при воздействии на них гармонических сигналов. формально частотные характеристики получаются из передаточной функции W(s) при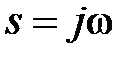 
, где
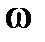– угловая частота, имеющая размерность [рад/с]. Сделав такую замену, получим
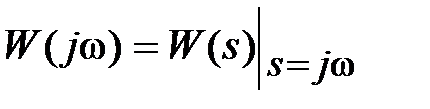
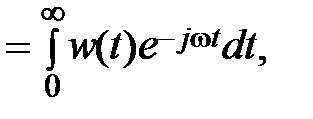(2.13)
т.е. частотная передаточная функция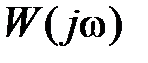 
есть прямое преобразование Фурье от весовой функции w(t).
Комплекснозначную функцию 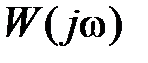частоты 
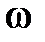будем называть амплитудно-фазовой частотной x а p акт ep истикой (АФЧХ) звена.
Как любое комплексное число АФЧХ можно представить в виде
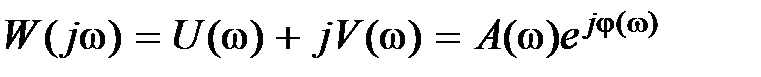, (2.14)
где
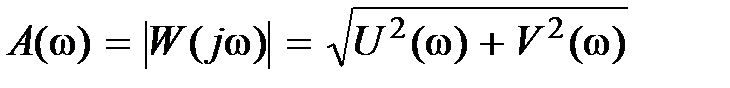, (2.15)
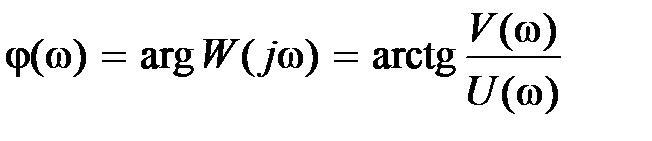. (2.16)
Если передаточная функция звена представлена в виде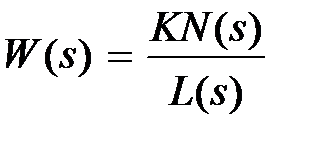 
, то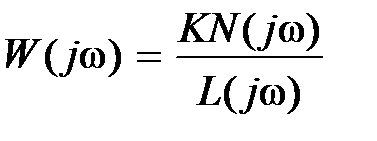 
. При этом, очевидно, 
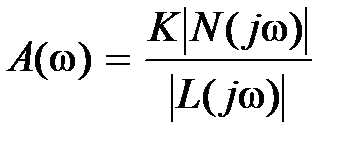(считаем 
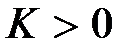) и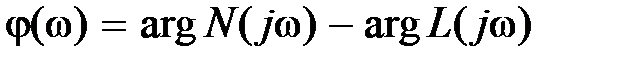 
.
В соответствии с (2.14)–(2.16) имеем еще ряд частотных характеристик: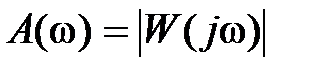 
– амплитудно-частотная x а p акт ep истика (АЧХ);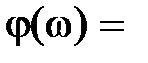 
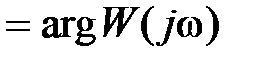– фазово-частотная x а p акт ep истика (ФЧХ); 
, 
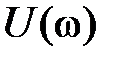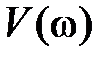– соответственно в e ществ e нная и мнимая частотные характеристики.
Рассмотрим физический смысл частотных характеристик. Если на вход звена с передаточной функцией W(s) поступает гармонический сигнал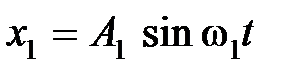 
, то в установившемся режиме после затухания переходной составляющей выходной сигнал 
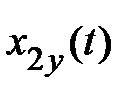будет также гармоническим: 
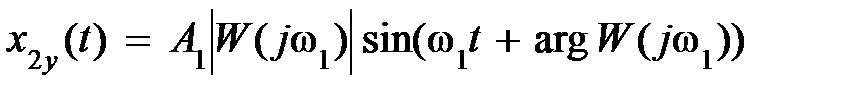, т.е. той же частоты, но измененных амплитуды и фазы.
Изменение амплитуды определяется модулем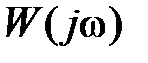 
, а фазы – аргументом 
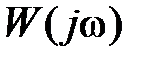на соответствующей частоте 
.
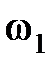На практике для наглядности частотные характеристики изображают в виде графиков при изменении частоты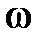 
от 0 до 
.
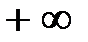Частотные характеристики обладают следующими свойствами: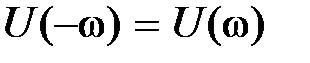 
, 
, 
, 
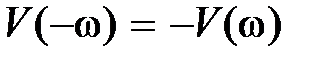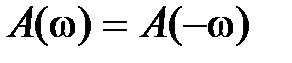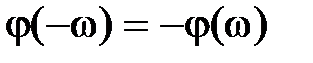, которые непосредственно следуют из (2.14)–(2.16). Другими словами: характеристики 
, 
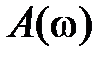являются четными, 
, 
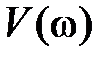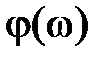– нечетными. В силу этого графики при изменении частоты oт –∞ до 0 не строятся. АФЧХ 
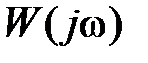представляет собой годограф на комплексной плоскости с координатами u, v или А, 
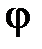при изменении 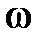от 0 до 
.
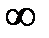На рис. 2.4 и 2.5 представлены иллюстративные графики частотных характеристик некоторого звена.
Рис. 2.4
Штриховой линией показаны части графиков, соответствующие 
. Вполне понятно, что из графика (см. рис. 2.4) нетрудно получить графики а, б или соответственно в, г (см. рис. 2.5) и наоборот.
Рис. 2.5
На практике часто применяются соответствующие логарифмические частотные характеристики: лога p ифмич e ская амплитудная частотная характеристика (ЛАЧХ)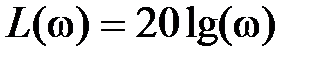 
и логарифмическая фазовая частотная x а p акт ep истика (ЛФЧХ) 
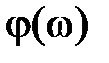, графики которых строятся в логарифмическом масштабе. При построении 
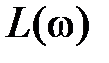по оси ординат откладывается величина 
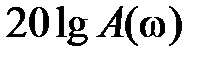, единицей измерения которой является децибел, а по оси абсцисс –
частота 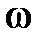[1/с] в логарифмическом масштабе, т.е. величина 
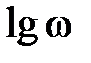. Увеличение 
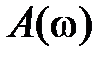в 10 раз соответствует приращению 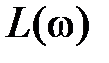вдоль оси ординат на 20 дБ. При построении ЛФЧХ величину 
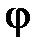откладывают по оси ординат в обычном масштабе (в градусах или радианах), a 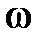– в логарифмическом масштабе.
На рис. 2.6 приведены иллюстративные графики ЛАЧХ и ЛФЧХ для некоторого звена. Частота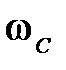 
, при которой 
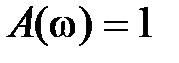, носит название частоты среза. Левее 
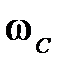значения 
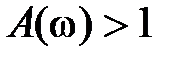(усиление), правее – 
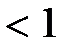(ослабление амплитуды гармонического сигнала).
Рис. 2.6
6. Элементарные звенья: идеальное интегрирующее звено.