Второй принцип управления – это п p инцип комп e нс a ции (уп p авл e ни e по возмущ e нию). Структура системы управления представлена на рис. 1.5.
1. Классификация систем автоматического управления, принципы управления.
Классификацию систем автоматического управления осуществляют в зависимости от признаков, в качестве которых могут быть принципы работы, алгоритмы функционирования, структуры систем, вид представления отдельных элементов, вид математических моделей, области применения и др.
По виду алгоритмов функционирования системы автоматического управления делятся на системы стабилизации (V = const, поддерживается некоторое постоянное значение выхода Y, рис. 1.8), системы программного управления (вход V должен изменяться по заданной программе), следящие системы – закон изменения входного сигнала v неизвестен заранее. Примерами таких систем соответственно являются системы стабилизации скорости вращения и частоты; система автоматического управления промышленного робота, работающая в режиме отработки заданных (программных) движений; радиолокационные следящие системы измерения координат движущегося объекта. С развитием практики и теории автоматического управления появляются новые классы систем: системы с поиском экстремума показателя качества, системы оптимального упр a вления, адаптивны e сист e мы.
Приведем классификацию систем по виду законов управления. под законом управления будем понимать зависимость выходного сигнала регулятора u от сигнала ошибки e. Для простоты примем, что u и Е – скалярные величины, которые обозначим малыми буквами; тогда в общем случае закон управления будет иметь вид: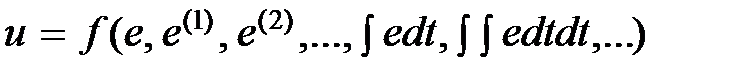 
.
Простейшими случаями этого соотношения являются:
- п р опо р циональный закон (П-закон):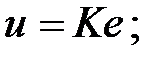 
- интегральный закон (И-закон):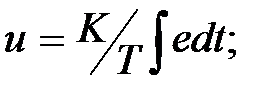 
- пропорционально-интегральный закон (ПИ-закон):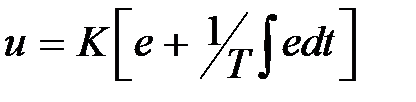 
;
- п p опо p ционально-инт e гально-дифф epe нциальный закон (ПИД-закон):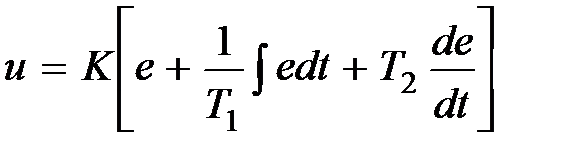 
,
где K – коэффициент передачи; а T, T1, T2 – постоянные времени.
По количеству управляемых координат системы делятся на одномерны e
( 
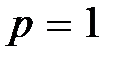) и многоме p ны e, или многосвязны e ( 
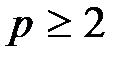) (см. рис. 1.1).
По характеру протекающих процессов системы делятся на непрерывные (все сигналы непрерывны во времени) и импульсные (хотя бы один из сигналов дискретизирован (квантован) во времени). Если хотя бы один из сигналов в системе является квантованным по уровню, то она относится к релейным системам. При одновременном квантовании сигнала по уровню и времени систему относят к цифровым. Релейные, импульсные и цифровые системы составляют класс дискретных систем автоматического управления.
По зависимости выходных сигналов отдельных элементов от входных системы делятся на линейные и нелинейные.
По виду параметров, характеризующих отдельные элементы и устройства, системы делятся на системы с сосредоточенными или распределенными параметрами, стационарные (все параметры постоянны во времени), нестационарные (параметры изменяются во времени), системы с детерминированными параметрами (закон изменения параметров известен), со случайными (стохастическими) параметрами (заданы их вероятностные характеристики), с неопределенными параметрами (может, например, задаваться только область их изменения).
Приведенная классификация не охватывает всех классов существующих систем. Например, можно выделять еще системы с запаздыванием, системы с перестраиваемой структурой. Адаптивные системы делятся на самонастраивающиеся и самоорганизующиеся.
В основу функционирования систем автоматического управления положены три основных принципа управления
Принцип разомкнутого управления соответствует структуре, изображенной на рис. 1.4. По этому принципу управляющее устройство формирует сигнал управления без учета информации о возмущениях и о результатах управления. Этот простейший принцип применим только в том случае, если возмущения определены и учтены на предварительной стадии при формировании алгоритма управления и объект управления строго исполняет предписанный алгоритм управления.
Второй принцип управления – это п p инцип комп e нс a ции (уп p авл e ни e по возмущ e нию). Структура системы управления представлена на рис. 1.5.
1.4 1.5
В этом случае вся информация о действующих возмущениях непрерывно поступает на управляющее устройство и учитывается при выработке алгоритма управления. Недостатками этого принципа являются техническая сложность, а иногда невозможность измерить возмущение, а также – отсутствие информации о результатах управления.
третий принцип управления – принцип обратной связи (управление по отклонению). Структура системы автоматического управления в данном случае представлена на рис. 1.6. В системе существует канал передачи информации о результатах управления – канал обратной связи. При этом косвенно через объект управления учитывается и влияние возмущений на вектор выхода. В этом случае алгоритм управления непрерывно учитывает результаты управления.
2. Уравнения звеньев.
Система автоматического управления (САУ) – это совокупность соединенных в определенной последовательности элементов и устройств, которые будем называть звеньями. Примерами звеньев могут служить объекты управления, усилительно-преобразовательные устройства, исполнительные двигатели, тахогенераторы, различного рода датчики, цифровые устройства, в том числе микропроцессоры и управляющие ЭВМ и т.п.
Под линейной непрерывной стационарной системой с сосредоточенными параметрами будем понимать систему, которая в целом так же, как и отдельные звенья, описывается линейными обыкновенными дифференциальными уравнениями с постоянными коэффициентами.
На рис. 2.1 изображено звено САУ, имеющее один входной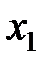 
и один
выходной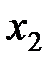 
сигналы, являющиеся скалярными величинами ( 
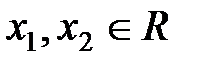, где
R – множество действительных или комплексных чисел). В дальнейшем будем интерпретировать все сигналы в системе как функции текущего времени t, т.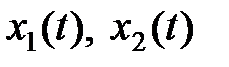е. 
, где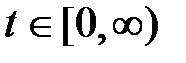 
.
|
| Получение уравнений, описывающих поведение отдельных звеньев в каждом конкретном случае, является задачей той или иной отрасли науки, например, электротехники, электроники, механики и т.п. и не является предметом данного курса. Поэтому будем по- |
лагать, что звено в общем случае описывается дифференциальным уравнением следующего вида:
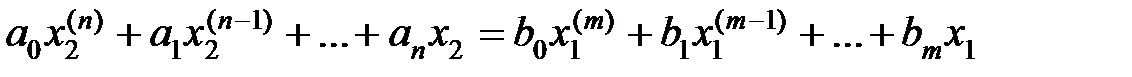, (2.1)
где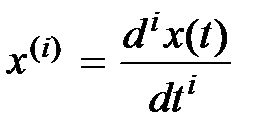 
; 
.
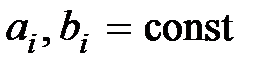Коэффициенты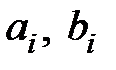 
зависят от конструктивных параметров и, возможно, от режима работы звена. Порядок n дифференциального уравнения (2.1) будет определять также и соответствующий порядок звена. На практике звенья описываются дифференциальными уравнениями низкого порядка, обычно 
.
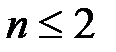Для полного математического описания процессов в звене следует задавать начальные условия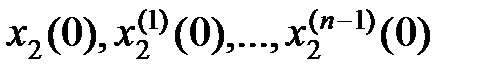 
, которые чаще всего будем полагать нулевыми.
В теории автоматического управления наряду с (2.1) уравнения звеньев записывают в стандартной форме, когда коэффициенты при переменных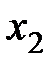 
и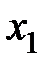 
равны единице. Вынося за скобк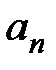и 
и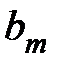 
, имеем
,
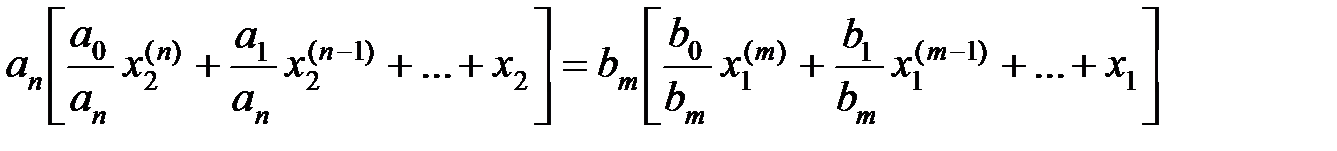или, вводя обозначения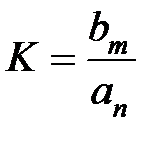 
, 
, 
…; 
, 
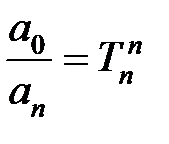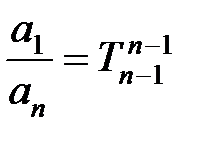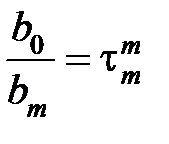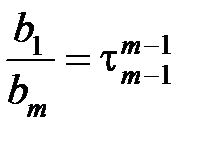,…, получим следующий вид дифференциального уравнения:
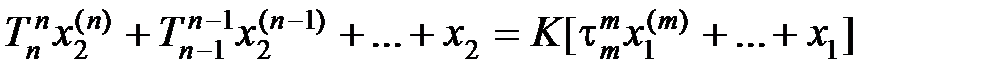, (2.2)
где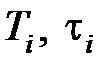 
– постоянные врем e ни, имеющие размерность [с], а K – коэффициент п epe дачи (усил e ния) имеет размерность [разм. х2 / разм. х1].
Уравнения (2.1) и (2.2) можно записать также в операторном (символическом) виде, вводя дифференциальный оператор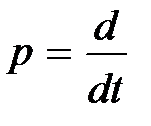 
такой, что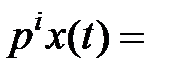 
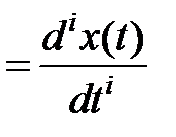. Тогда уравнение (2.1) может быть записано в операторной форме: 
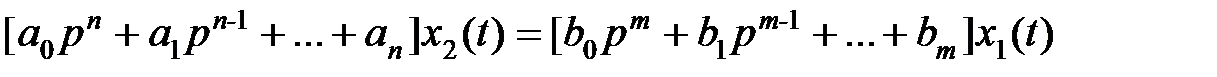. обозначая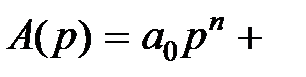 
, 
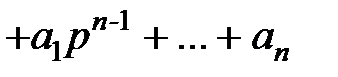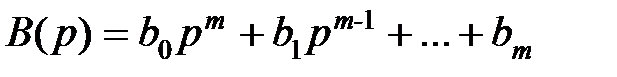, будем иметь
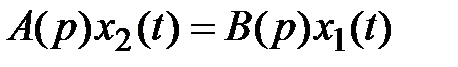. (2.3)