Рис. 10.1. Зависимость общей суммы затрат от объема производства
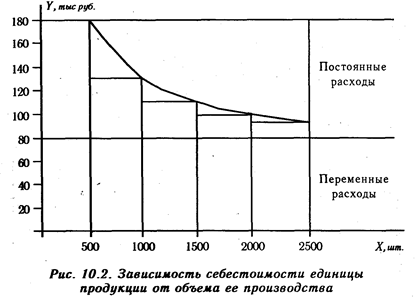
Иная ситуация показана на рис. 10.2, где для каждого объема производства сначала отложены уровни переменных расходов на единицу продукции, а затем суммы постоянных расходов. Соединив значения переменных расходов, получим прямую, параллельную оси абсцисс, а после соединения уровней постоянных расходов — кривую себестоимости единицы продукции, которая при увеличении объема производства постепенно приближается к прямой переменных расходов, а при спаде производства она будет стремительно подниматься.
Очень важное значение имеет точное определение суммы постоянных и переменных затрат, так как. от этого во многом зависят результаты анализа. Для этой цели используются разные методы: алгебраический, графический, статистический, основанный на корреляционно-регрессионном анализе, содержательный, построенный на основе анализа каждой статьи и элементов затрат.
Алгебраический метод можно применять при наличии информации о двух точках объема продукции в натуральном выражении (х1 и x2) и соответствующих им затратах (z1 и z 2 ). Переменные затраты на единицу продукции ( b ) определяют следующим образом:
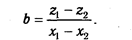
Узнав переменные затраты на единицу продукции, нетрудно подсчитать сумму постоянных затрат (о):
а = z 2 – bх2, или а = z1 – b x1.
Например, максимальный объем производства продукции, который может обеспечить предприятие, составляет 2000 шт. При таком объеме производства общая сумма затрат - 250 млн руб. Минимальному объему производства, равному 1500 шт., соответствует общая сумма издержек на сумму 200 млн руб.
Вначале определим переменные издержки на единицу продукции:
(250 - 200)/(2000 - 1500) = 0,1 млн руб.
Затем найдем общую сумму постоянных затрат:
250 - 0,1 х 2000 = 50 млн руб., или 200 - 0,1 х 1500 = 50 млн руб.
Уравнение затрат для данного примера будет иметь вид
Y = 50 + 0,1x.
По этому уравнению можно спрогнозировать общую сумму затрат для любого объема производства в заданном релевантном ряду.
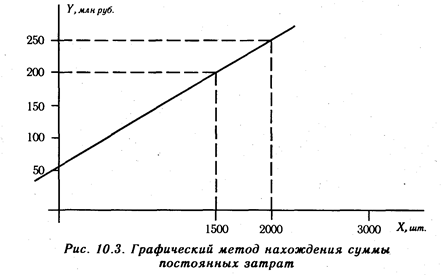
Графический метод нахождения суммы постоянных затрат состоит в следующем. На графике откладываются две точки, соответствующие общим издержкам для минимального и максимального объема производства (рис. 10.3). Затем они соединяются до пересечения с осью ординат, на которой откладываются уровни издержек. Точка, где прямая пересекает ось ординат, показывает величину постоянных затрат, которая будет одинаковой как для максимального, так и для минимального объема производства.
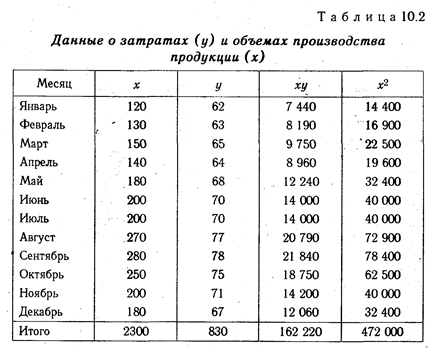
Уравнение общей суммы затрат ( Y = а + b х) можно получить и с помощью корреляционного анализа, если имеется достаточно большая выборка данных о затратах и выпуске продукции (табл. 10.2).
Составим систему уравнений и решим ее:
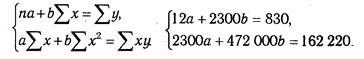
Умножив все члены первого уравнения на 2300, а второго на 12, получим следующую систему уравнений:
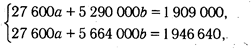
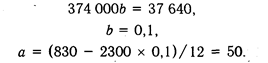
Уравнение связи Y = 50 + 0,1х показывает, что сумма постоянных затрат на данном предприятии составляет 50 млн руб., а переменные затраты на единицу продукции - 100 тыс. руб.
10.3. Анализ функциональной связи между затратами, объемом продаж и прибылью. Определение безубыточного объема продаж и зоны безопасности предприятия








