Сущность и значение моделирования, требования к нему. Основные типы факторных детерминированных моделей. Способы преобразования факторных моделей. Правила моделирования.
Одной из задач факторного анализа является моделирование взаимосвязей между результативными показателями и факторами, которые определяют их величину.
Моделирование - это один из важнейших методов научного познания, с помощью которого создается модель (условный образ) объекта исследования. Сущность его заключается в том, что взаимосвязь исследуемого показателя с факторными передается в форме конкретного математического уравнения.
В факторном анализе различают модели детерминированные (функциональные) и стохастические (корреляционные). С помощью детерминированных факторных моделей исследуется функциональная связь между результативным показателем (функцией) и факторами (аргументами).
При моделировании детерминированных факторных систем необходимо выполнять ряд требований.
1. Факторы, включаемые в модель, и сами модели должны иметь определенно выраженный характер, реально существовать, а не быть придуманными абстрактными величинами или явлениями.
2. Факторы, которые входят в систему, должны быть не только необходимыми элементами формулы, но и находиться в причинно-следственной связи с изучаемыми показателями. Иначе говоря, построенная факторная система должна иметь познавательную ценность. Факторные модели, которые отражают причинно-следственные отношения между показателями, имеют значительно большее познавательное значение, чем модели, созданные при помощи приемов математической абстракции. Последнее можно проиллюстрировать следующим образом. Возьмем две модели:
1)ВП=ЧРхГВ:
2)ГВ=ВП/ЧР, где ВП - валовая продукция предприятия; ЧР - численность работников на предприятии; ГВ — среднегодовая выработка продукции одним работником.
В первой системе факторы находятся в причинной связи с результативным показателем, а во второй — в математическом соотношении. Значит, вторая модель, построенная на математических зависимостях, имеет меньшее познавательное значение, чем первая.
3. Все показатели факторной модели должны быть количественно измеримыми, т.е. должны иметь единицу измерения и необходимую информационную обеспеченность.
4. Факторная модель должна обеспечивать возможность измерения влияния отдельных факторов, это значит, что в ней должна учитываться соразмерность изменений результативного и факторных показателей, а сумма влияния отдельных факторов должна равняться общему приросту результативного показателя.
В детерминированном анализе выделяют следующие типы наиболее часто встречающихся факторных моделей.
1. Аддитивные модели:
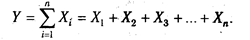
Они используются в тех случаях, когда результативный показатель представляет собой алгебраическую сумму нескольких факторных показателей.
2. Мультипликативные модели:
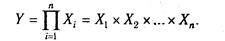
Этот тип моделей применяется тогда, когда результативный показатель представляет собой произведение нескольких факторов.
3. Кратные модели:
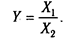
Они применяются тогда, когда результативный показатель получают делением одного факторного показателя на величину другого.
4. Смешанные (комбинированные) модели - это сочетание в различных комбинациях предыдущих моделей:
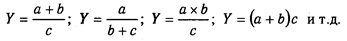
Моделирование мультипликативных факторных систем в АХД осуществляется путем последовательного расчленения факторов исходной системы на факторы-сомножители. Например, при исследовании процесса формирования объема производства продукции (см. рис. 5.2) можно применять такие детерминированные модели, как:
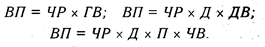
Эти модели отражают процесс детализации исходной факторной системы мультипликативного вида и расширения ее за счет расчленения на сомножители комплексных факторов. Степень детализации и расширения модели зависит от цели исследования, а также от возможностей детализации и формализации показателей в пределах установленных правил.








