Другое направление комплексной оценки - разработка алгоритмов вычислительных процедур, которые бы на основе комплекса показателей обеспечили однозначную оценку результатов хозяйственной деятельности.
Для решения этой задачи довольно широко используются алгоритмы, основанные на методах "суммы мест", геометрической средней и т.д. Но эти методики имеют существенный недостаток, потому что в них не учитываются весомость определенных показателей и степень различий в их уровне. Наиболее перспективным подходом является использование многомерного сравнительного анализа, основанного на методе эвклидовых расстояний, который позволяет учитывать не только абсолютные величины показателей каждого предприятия, но и степень их близости (дальности) до показателей предприятия-эталона. В связи с этим необходимо координаты сравниваемых предприятий выражать в долях соответствующих координат предприятия-эталона, взятого за единицу.
Рассмотрим практическую сторону решения задачи многомерного сравнительного анализа.
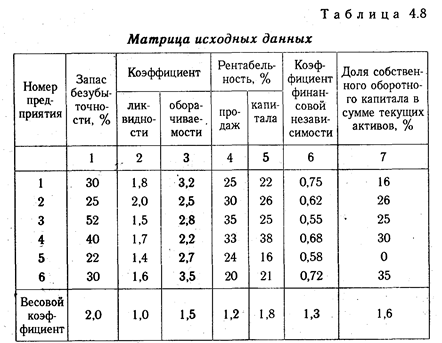
Этап 1. Обосновывается система показателей, по которым будут оцениваться результаты хозяйственной деятельности предприятий, собираются данные по этим показателям и формируется матрица исходных данных (табл. 4.8). Исходные данные могут быть представлены как в виде моментных показателей, отражающих состояние предприятия на определенную дату, так и темповых показателей, характеризующих динамику деятельности предприятия и представленных в виде коэффициентов роста. Возможно изучение одновременно и моментных, и темповых показателей.
Этап 2. В табл. 4.8 в каждой графе определяется максимальный элемент, который принимается за единицу. Затем все элементы этой графы (аij) делятся на максимальный элемент эталонного предприятия (max аy). В результате создается матрица стандартизованных коэффициентов (х ij ), представленных в табл. 4.9:
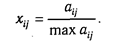
Эталонное предприятие формируется обычно из совокупности однородных объектов, принадлежащих к одной отрасли. Однако это не исключает возможности выбора предприятия-эталона из совокупности предприятий, принадлежащих к различным отраслям деятельности, так как многие финансовые показатели сопоставимы и для разнородных субъектов хозяйствования.
Если с экономической стороны лучшим является минимальное значение показателя (например, затраты на рубль товарной продукции), то надо изменить шкалу расчета так, чтобы наименьшему результату соответствовала наибольшая величина коэффициента.
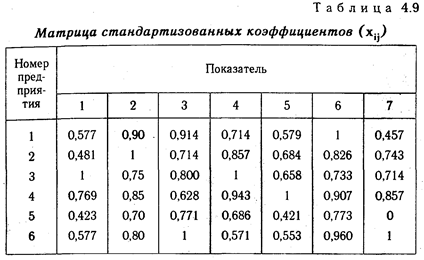
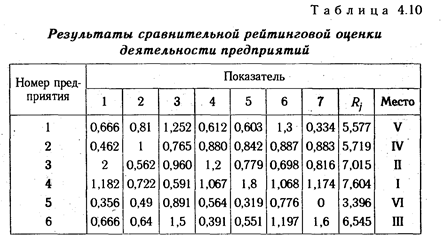
Этап 3. Все элементы матрицы координат возводятся в квадрат. Если задача решается с учетом разного веса показателей, тогда полученные квадраты умножаются на величину соответствующих весовых коэффициентов (К), установленных экспертным путем, после чего результаты суммируются по строкам (табл. 4.10):
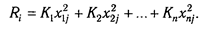
Этап 4. Полученные рейтинговые оценки ( Rj ) размещаются по ранжиру и определяется место каждого предприятия по результатам хозяйствования. Первое место занимает предприятие, которому соответствует наибольшая сумма, второе место предприятие, имеющее следующий результат, и т.д.
Подчеркнем некоторые преимущества предлагаемой методики многомерного сравнительного анализа.
Во-первых, рассмотренная методика базируется на комплексном многомерном подходе к оценке такого сложного явления, как производственно-финансовая деятельность предприятия.
Во-вторых, она учитывает реальные достижения всех предприятий-конкурентов и степень их близости к показателям предприятия-эталона.
В-третьих, предлагаемая методика делает количественно измеримой оценку надежности делового партнера, основанную на результатах его прошлой и текущей деятельности, что позволяет избежать субъективизма и более реально оценивать рейтинг предприятий.
4.3. Способы приведения показателей в сопоставимый вид








