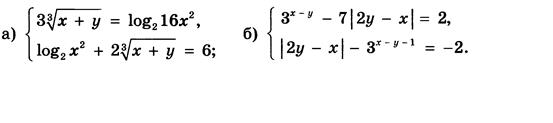Методические указания по выполнению задания 1 .

Дата: 2025-05-01; Просмотры: 2
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

- Вызовите формульный редактор;

- В палитре шаблонов выберите третий слева шаблон с индексами;

- В открывшемся списке выберите левый в первом ряду;

- Наберите греческое "Хи" (в палитре символов второе поле справа - греческие символы).

Обратите внимание на различный вид курсоров. Вводимый символ вставляется в позицию, определяемую вертикальной чертой курсора!

- Подведите курсор в поле верхнего индекса и нажмите 2;

- Введите "=" после Х;

- — из палитры шаблонов выберите знак суммы с верхним и нижним индексами, и введите индексы;

- Выберите из палитры шаблонов объект с верхним индексом (первый в четвёртом ряду);

- Выберите шаблон со скобками;

- Выберите шаблон для дроби;

- — Выберите шаблон с нижним индексом, введите Хи, переведите курсор в следующую позицию (стрелкой -> или шелчком мыши), наберите "-", затем "m"

- В знаменателе введите "s"

- В месте верхнего индекса наберите 2;

- Выйдите из редактора формул, щёлкнув левой кнопкой мыши вне поля редактирования.

- Сохраните формулу в файле.

 

Задание 2.

Наберите систему линейных уравнений в матричной записи в виде:

 

 

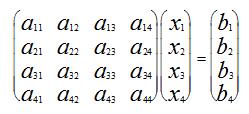
Рис.2. Матричная запись системы уравнений.

Методические указания по выполнению задания 2 .

- в новом окне вызовите формульный редактор;

- из палитры шаблонов выберите круглые скобки;

- выберите шаблон матрицы размером 4x4;

- перемещаясь от поля к полю с помощью мыши или клавиши tab, заполните матрицу;

- выберите круглые скобки, вектор размером 4, заполните его значениями;

- введите "=";

- аналогично введите последний вектор;

- выйдите из редактора формул;

- сделайте подпись под матрицей;

- сохраните рисунок в файле.

 

 

Задание 3:

Записать формулы с помощью формульного редактора Equation Editor :

1. 2xy dx + (x2 - y2)dy = 0. 2. y2(y dx - 2x dy) = x3(x dy - 2y dx).
3. (2x3y2 - y)dx + (2x2y3 - x)dy = 0. 4. (x2 - y)dx + x(y + 1)dy = 0.
5. (2x2y3 - 1)y dx + (4x2y3 - 1)x dy = 0. 6. (x2 + 1)(2x dx + cos y dy) = 2x sin y dx.
7. (x2 - sin2y)dx + x sin 2y dy = 0. 8. x(ln y + 2 ln x - 1)dy = 2y dx.
9. (x2 - y2 + y)dx + x(2y - 1)dy = 0. 10. (2x2y2 + y)dx + (x3y - x)dy = 0.
11. y dx - x dy = 2x3 tg(y/x) dx. 12. y2dx + (xy + tg xy)dy = 0.
13. y2dx + (ex - y)dy = 0. 14. y dy = (x dy + y dx) sqrt(1 + y2).
15. 2x(1 + sqrt(x2 - y)dx - sqrt(x2 - y)dy = 0. 16. (1 + y2 sin 2x)dx - 2y cos2x dy = 0.
17. e-ydx - (2y +xe-y)dy = 0. 18. (x/sin y + 2)dx + ((x2 + 1)cos y)/(cos 2y - 1) dy = 0.
19. (2 - 9xy2)x dx + (4y2 - 6x3)y dy = 0. 20. y(y2 + 1)dx + x(y2 - x + 1)dy = 0.
21. ((3x2 + y2)/y2)dx - ((2x3 + 5y)/y3)dy... 22. 3x2(1 + ln y)dx = (2y - x3/y)dy.
23. (y/x)dx + (y3 + ln x)dy = 0. 24. (x2 + 2x + y)dx = (x - 3x2y)dy.
25. x2y(y dx + x dy) = 2y dx + x dy. 26. (y - 1/x)dx + dy/y = 0.
27. y(x + y2)dx + x2(y - 1)dy = 0. 28. x2y3 + y + (x3y2 - x)y' = 0.
29. y2dx - (xy + x3)dy = 0. 30. xy dx = (y3 + x2y + x2)dy.

 

Задание 4: Записать формулы с помощью формульного редактора Equation Editor.

Вариант 1:

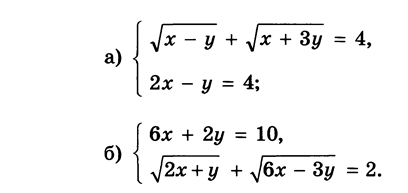
Вариант 2:

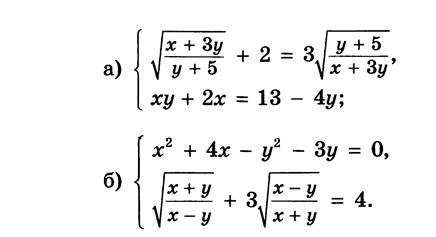
Вариант 3:

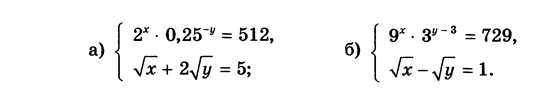
Вариант 4:

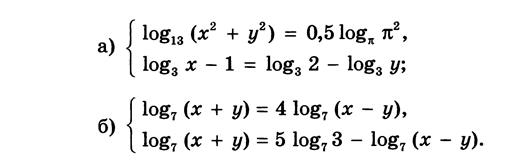
Вариант 5: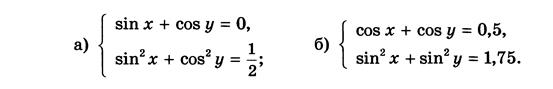

 

 

Вариант 6:

 

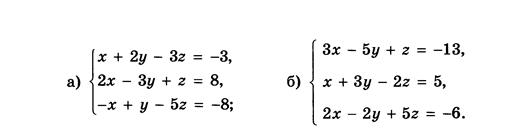
Вариант 7:

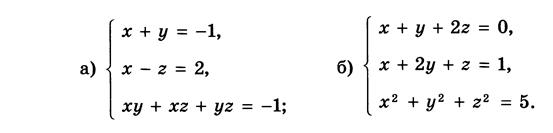
Вариант 8:

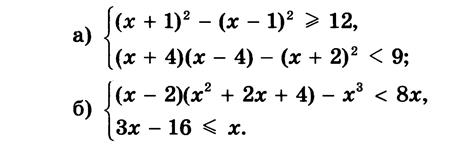
Вариант 9:

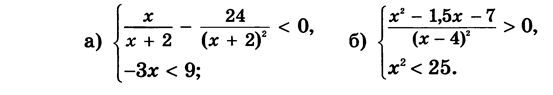
Вариант 10:

 

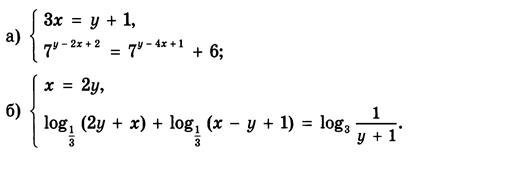
Вариант 11:

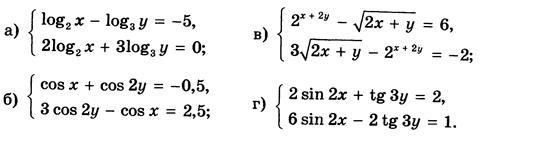
Вариант 12:

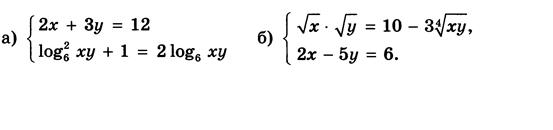
Вариант 13: