Среднее квадратическое отклонение
Среднее квадратическое отклонение: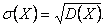 
Среднее квадратическое отклонение равно корню квадратному из дисперсии, поэтому его размерность равна размерности случайной величины. Например, если Х выражается в линейных метрах, то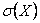 
тоже выражается в линейных метрах, а D(X) – в квадратных метрах.
Примеры решения задач
Задача 1. Закон распределения вероятностей дискретной случайной величины дан в виде таблицы. Найти математическое ожидание этой величины.
| Х | – 4 | – 3 | – 2 | – 1 | 0 | 1 | 2 | 3 | 4 |
| Р | 0,02 | 0,03 | 0,1 | 0,15 | 0,4 | 0,15 | 0,1 | 0,03 | 0,02 |
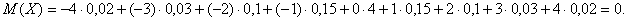
Задача 2. Найти дисперсию случайной величины Х
| X | 2 | 3 | 5 |
| P | 0,1 | 0,6 | 0,3 |
M(X) = 2 . 0,1 + 3 . 0,6 + 5 . 0,3 = 3,5.
| X2 | 4 | 9 | 25 |
| P | 0,1 | 0,6 | 0,3 |
M(X2) = 4 . 0,1 + 9 . 0,6 + 25 . 0,3 = 0,4 + 5,4 + 7,5 = 13,3
D(X) = M(X)2 – (M(X))2 = 13,3 – (3,5)2 = 1,05
Задача 3. Дискретная случайная величина Х имеет закон распределения, приведенный в таблице:
| X | 0,2 | 0,4 | 0,6 | 0,8 | 1 |
| P | 0,1 | 0,2 | 0,4 |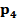 
| 0,1 |
Чему равна вероятность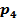 
(случайная величина Х принимает значение 0,8)? Построить многоугольник распределения.
Решение. Поскольку должно выполняться равенство (1):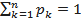 
, т.е. 
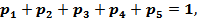то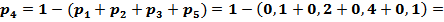 
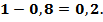
Следовательно,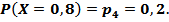 
Многоугольник распределения изображен на рисунке:
 |
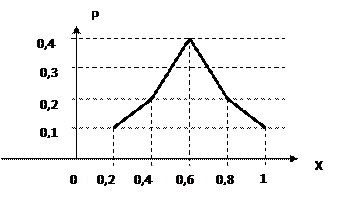Задача 4. Подбрасываются две симметричные монеты, подсчитывается число гербов на обеих верхних сторонах монет. Рассматривается дискретная случайная величина Х - число выпадений гербов на обеих монетах. Записать закон распределения случайной величины Х.
Решение. В данном опыте четыре равновозможных элементарных
исхода: (Г,Г), (Г,Ц), (Ц,Г), (Ц,Ц). Запись, например, (Г, Ц) означает, что на первой монете выпал герб, на второй – цифра, аналогичный смысл имеют остальные записи. Герб может выпасть 1 раз, 2 раза или не появиться ни разу. Следовательно, случайная величина Х может принимать только три значения: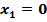 
, 
, 
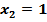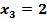. Найдем вероятности появления этих значений Х:
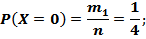
где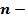 
общее число равновозможных элементарных исходов,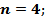 
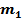- число благоприятствующих данному событию исходов. 
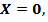т.е. герб не выпадает ни на одной монете (комбинация Ц,Ц), следовательно,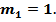 
Рассуждая аналогично, находим: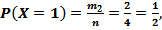 
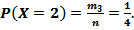
Получили: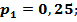 
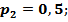
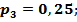причем, 
.
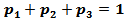Таким образом, закон распределения данной случайной величины
можно задать таблицей:
| X | 0 | 1 | 2 |
| P | 0,25 | 0,5 | 0,25 |
Самостоятельная работа:
Задача 1. Для проведения лотереи изготовили 200 билетов. Из них 2 билета с выигрышем 500 рублей, 10 билетов по 100 руб и остальные по 5 рублей (беспроигрышная лотерея). Наудачу выбирают билет. Найти математическое ожидание выигрыша.
Задача 2. Дискретная случайная величина Х имеет закон распределения, приведенный в таблице:
| X | 0,2 | 0,3 | 0,5 | 0,7 | 1 |
| P | 0,1 | 0,2 | 0,3 |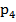 
| 0,1 |
Чему равна вероятность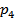 
(случайная величина Х принимает значение 0,7)? Построить многоугольник распределения.
Задача 3. Дано распределение случайной величины Z
| Значения | – 4 | 0 | 6 |
| Вероятность | 0,3 | 0,5 | 0,2 |
Вычислить дисперсию этой случайной величины.
Задача 4. Дисперсия случайной величины Х равна 3. Найдите D(Y), где
а) Y = 3X; б) Y = X + 5; в) y – 4X; г) Y = 2X – 1; д) Y = 5 – 3X; е) Y = – 5X – 7.
Контрольные вопросы:
1. Что называется математическим ожиданием случайной величины?
2. Что называется дисперсией случайной величины?
3. В чём состоит закон распределения случайной величины?
4. Что такое мода, медиана и среднее значение случайной величины?