Тема: «Элементы математической статистики».

Дата: 2025-06-15; Просмотры: 1

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Практическое занятие №13

Тема: «Элементы математической статистики».

Цели урока:

• рассмотреть примеры задач математической статистики
• отработать навыки нахождения основных числовых характеристик для небольших наборов дискретных случайных величин;
• рассмотреть свойства математического ожидания, дисперсии.

Знать основные числовые характеристики случайной величины.

Уметь применять формулы к решению задач.

Теоретический минимум

Основными числовыми характеристиками случайной величины являются:

• математическое ожидание;
• мода;
• медиана;
• дисперсия;
• среднее квадратическое отклонение.

Рассмотрим эти характеристики для дискретной случайной величины.

Математическое ожидание

Определение: Математическим ожиданием (ожидаемым значением или средним значением) дискретной случайной величины называют число M(X) = x₁p₁ + x₂p₂ + ...+ x_np_n – сумму произведений всех ее возможных значений на их вероятности.
Математическое ожидание измеряется в тех же единицах, что и сама величина.
Свойства математического ожидания

• Математическое ожидание постоянной величины равно самой этой величине M(C) = C
• Постоянный множитель можно выносить за знак математического ожидания M(CX) = CM(X)
• Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий M(XY) = M(X) ^. M(Y)
• Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий M(X + Y) = M(X) + M(Y)

Дисперсия

Дисперсия – это среднее арифметическое квадратов разностей между значениями случайной величины и ее средним значением. В наших обозначениях:

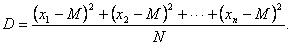
Или в общем виде дисперсией дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее среднего значения.

Формула для вычисления дисперсии

D(X) = M(X)² – [M(X)]²

Свойства дисперсии

1. Дисперсия постоянной величины равна нулю D(C) = 0

2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат D(CX) = C²D(X)

3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин D(X + Y) = D(X) + D(Y)

4. Дисперсия разности двух независимых величин равна сумме их дисперсий D(X – Y) = D(X) + D(Y)

Следствия

5. D(C + X) = D(X) где С – const.

6. D(X + Y + Z) = D(X) + D(Y) + D(Z)