Symsum (an, n, n1, n2) – функция суммирования числовых рядов
1 Цель работы
1) Получение первых навыков работы с системой компьютерной математики MATLAB.
2) Знакомство с основными операциями над векторами и матрицами в MATLAB.
3) Знакомство с простейшими графическими средствами MATLAB.
4) Решение задачи по вычислению суммы числового ряда и анализу погрешностей полученных результатов.
2 Задание
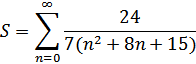
1) Найти сумму ряда аналитически
2) Вычислить значения частичных сумм ряда
3) Найти величину погрешности при значениях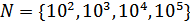 
4) Определить количество верных цифр результатов
3 Ход работы
3.1 Находим сумму ряда S аналитически с использованием средств Matlab:
>> syms n
>> S_inf=symsum(24/(7*(n^2+8*n+15)),n,0,inf)
S _ inf =
1
>>
Symsum (an, n, n1, n2) – функция суммирования числовых рядов
где an- член числового ряда, n - переменная суммирования, n1 - начальное значение переменной суммирования, n2 - конечное значение переменной суммирования;
С помощью функции symsum на данном этапе определена сумма ряда (24/(n^2+8*n+15)), значение которой присвоено переменной S_inf и равняется 8.
3.2 Находим значение частичных сумм S(N):
>> syms N
>> S=symsum(24/(n^2+8*n+15),n,0,N)
и в результате получаем:
S =-12/7*(9+2*N)/(N+5)/(N+4)+1
3.3 Формируем вектор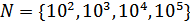
>> N=[10^2, 10^3, 10^4, 10^5]
N =
100 1000 10000 100000
3.4 Вычисляем значения частичных сумм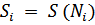 
ряда при соответствующих значениях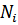 
>> S =-12/7*(9+2*N)/(N+5)/(N+4)+1
Результаты вычисления занесены в таблицу 1
Таблица 1 – Значения частных сумм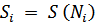 
| i |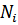
| 
|
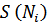
| 1 | 100 | 60.9672 |
| 2 | 1000 | 60.9966 |
| 3 | 10000 | 60.9997 |
| 4 | 100000 | 61.0000 |
3.5 Для каждой величины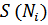 
определяем абсолютную погрешность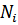
Для вычисления абсолютной погрешности будем использовать встроенную функцию abs:
>> D=abs(S-8)
D =
52.9672 52.9966 52.9997 53.0000
>> format long
>> D
D =
52.96718995290424 52.99658678717964 52.99965729707260 52.99996571582850
>> format short e
>> D
D =
5.2967e+001 5.2997e+001 5.3000e+001 5.3000e+001
Округленные результаты абсолютной погрешности занесены в таблицу 2.
Таблица 2 – Абсолютные погрешности
| 
| 
| 
|
| 
| 
| 
|
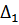
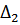
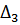
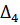
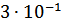
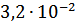
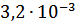
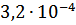
3.6 Для каждой величины 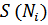вычислим относительную погрешность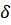 
>> d=D/8
d =
6.6209e+000 6.6246e+000 6.6250e+000 6.6250e+000
Округленные результаты относительной погрешности занесены в таблицу 3.
Таблица 3 – Относительные погрешности
| 
| 
| 
|
| 
| 
| 
|
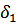
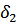
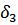
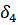
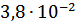
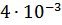
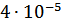
3.7 Для каждой величины 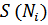определим количество верных цифр.
>> a=[1 1 1 1]
>> n=1-log10(a.*d)
n =
1.7908e-001 1.7884e-001 1.7882e-001 1.7881e-001
>> n=floor(n)
n =
0 0 0 0
3.8 Запишем численные значения найденных частичных сумм, округлив их до найденного ранее количества верных цифр.
>> format long
>> S
S =
60.96718995290424 60.99658678717964 60.99965729707260 60.99996571582850
Округленные окончательные результаты вычислений занесены в таблицу4.
Таблица 4 – Результаты вычисления S
| 
| 
| 
|
| 
| 
| 
|
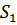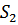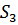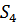
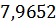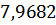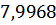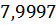