Решение задач Коши с помощью m at l ab
В.Ю. БЕЗРУКОВА,
Студентка 2 курса направления подготовки «Прикладная информатика»
Н.Ф. СТИФУТИНА,
старший преподаватель Алматинского филиала Санкт-ПетербургскогоГуманитар-ного университета профсоюзов - руководитель
РЕШЕНИЕ ЗАДАЧ КОШИ С ПОМОЩЬЮ M AT L AB
Дифференциальное уравнение — это уравнение, связывающее значение производной функции с самой функцией, значениями независимой переменной, числами.
Если в ДУ задано начальное условие в виде y(x0)=y0, то такое уравнение называется задачей Коши. В общее решение уравнения подставляют значения y0 и x0 и находят значение произвольной постоянной C, а затем частное решение уравнения при найденном значении C. Это и есть решение задачи Коши.
Иначе говоря, задача Коши является частным случаем линейного дифференциального уравнения, приводимым к линейному дифференциальному уравнению с постоянными коэффициентами, которое имеет простой алгоритм решения.
Решение таких примеров, поочередно выписывая каждое действие, у человека занимает много места на обычном листке бумаги и немало времени, при отсутствии должных навыков. В таких случаях удобнее использовать программу MatLab — пакет прикладных программ для различных технических вычислений и решения задач. При решении сложных задач явно видно преимущество MatLab.
Рассмотрим пример решения несложной задачи Коши обычным способом:
y''-3y'+2y=0;
y(0)=0, y'(0)=1;
λ2-3λ+2=0;
λ1,2 = 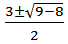 =
= 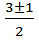 =[
=[ 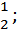
y=C1ex+C2e2x ;
y'=C1ex+2C2e2x ;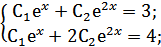
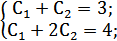
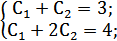
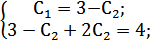
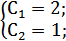 y2=2ex+e2x Задача Коши в MatLab записывается следующим образом:
y2=2ex+e2x Задача Коши в MatLab записывается следующим образом:
| > function dy=pr(x,y) | вводится функция с названием |
| > dy=zeros(2,1); | вводится массив значений |
| > dy(1)=y(2); | |
| > dy(2)=3.*y(2)-2.*y(1); | вводится само условие |
| > end | конец ввода функции |
| > [x,y]=ode45(@pr,[1 10], [3 4]); | вызов функции ode45[1] |
| > plot(x,y) | строится график функции |
| > grid; | нанесение сетки |
Решение задачи выдается в виде графика:Рис. 1 y''-3y'+2y=0 при y(0)=0, y'(0)=1, график 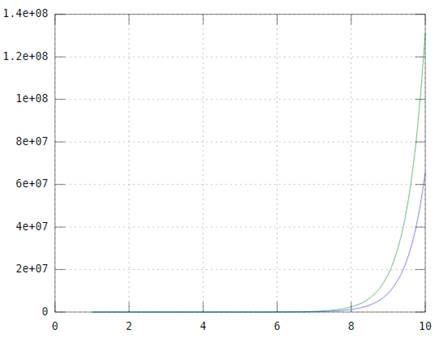 Для решения задач Коши в MatLab существует несколько функций: ode23, ode45, odell3, odel5s, ode23s, ode23t и ode23tb. Методика их использования одинакова, не изменяется и способ задания входных и выходных аргументов. Ode45, которая была использованы выше, является функцией, использующей метод Рунге-Кутта четвертого-пятого порядка точности с автоматическим выбором размера шага. MatLab популярен по всему миру, так как он упрощает процесс вычисления более сложных задач, чем рассмотренных здесь, а круг возможностей программы невероятно велик. В университетах MatLab используется как инструмент для работы в различных областях математики. В промышленности MatLab применяется для более продуктивных исследований, разработок и анализа данных . Больше всего он распространен среди инженеров и научных работников, в том числе его используют около трети всех исследователей. Одним из важнейших преимуществ MatLab является то, что он работает на большинстве современных операционных систем, распространенных и среди обычных пользователей.
Для решения задач Коши в MatLab существует несколько функций: ode23, ode45, odell3, odel5s, ode23s, ode23t и ode23tb. Методика их использования одинакова, не изменяется и способ задания входных и выходных аргументов. Ode45, которая была использованы выше, является функцией, использующей метод Рунге-Кутта четвертого-пятого порядка точности с автоматическим выбором размера шага. MatLab популярен по всему миру, так как он упрощает процесс вычисления более сложных задач, чем рассмотренных здесь, а круг возможностей программы невероятно велик. В университетах MatLab используется как инструмент для работы в различных областях математики. В промышленности MatLab применяется для более продуктивных исследований, разработок и анализа данных . Больше всего он распространен среди инженеров и научных работников, в том числе его используют около трети всех исследователей. Одним из важнейших преимуществ MatLab является то, что он работает на большинстве современных операционных систем, распространенных и среди обычных пользователей.
Список литературы:1. Курбатова Е. А. "Диалектика", 2006 г., 256 с2. Доля П.Г. «Использование MATLAB. Решение дифференциальных уравнений»., 52 c.3. Мироновский Л.А., Петрова К. Ю. «Введение в MatLab», 2005 г., 122 с.
Регистрационная карточка участника конференции
| 1. | Фамилия, имя, отчество участника Безрукова Вероника Юрьевна |
| 2. | Место учебы Алматинский филиал Санкт-Петербургского университета профсоюзов |
| 3. | Факультет / специальность, курс Экономический, прикладная информатика, 2 курс |
| 4. | Контактный телефон +7 707 0481852 |
| 5. | E-mail Ride_the_wave@bk.ru |
| 6. | Название тезисов Решение задач Коши с помощью MatLab |
| 7. | Предполагаемая тематическая секция Информатика и математика |
| 8. | Форма участия (очная / заочная) очная |
| 9. | Фамилия, имя, отчество научного руководителя Стифутина Нина Федоровна |
| 10. | Место работы, должность Алматинский филиал Санкт-Петербург-ского университета профсоюзов, старший преподаватель |
| 11. | Ученая степень, ученое звание |
| 12. | Контактный телефон научного руководителя +8 777 287 42 01 |
| 13. | * Все расходы для иногородних участников конференции за счет командирующей стороны |
[1]@pr – ссылка на функцию, [0 10]- интервалы интегрирования, [3 4] - условие: y(0)=0, y'(0)=1; функция ode45 возвращает решение в виде столбцов: первый столбец представляет выбранные значения независимого аргумента x, а второй и третий – значения функций y1 и y2








