План выполнения практической работы
Практическая работа № 4
Тема: «Производные высших порядков»
Цели:
· закрепить и систематизировать теоретические знания,
· формировать умения и навыки решения задач по нахождению производных и дифференциала высших порядков.
В результате выполнения работы студент должен знать определение дифференциала и производной функции высших порядков.
Должен уметь находить производные функции высших порядков.
Оборудование и учебные пособия: мультимедийный проектор, презентация к уроку;
Н. В. Богомолов, П. И. Самойленко «Математика». - М.: Дрофа, 2010 г.
План выполнения практической работы
1. Повторение основных теоретических сведений по данной теме
2. Изучение методических рекомендаций по решению задач и выполнение упражнений и задач .
3. Выполнение практической самостоятельной работы по вариантам.
4. Письменные ответы на контрольные вопросы
Задания для практической работы .
1. Краткие теоретические сведения.
Производная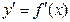 
от функции 
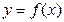называется производной первого порядка, или первой производной. Тогда производная от первой производной называется второй производной или производной второго порядка функции y=f(x) и обозначается 
, 
, 
.
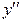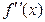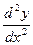Опр: Производной n-го порядка функции y = f ( x ), если она существует, называется производная от производной (n-1) - порядка;
, 
, 
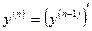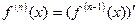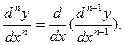
Производные высших порядков вычисляются последовательным дифференцированием данной функции.
2. Методические рекомендации по решению упражнений и задач.
Пример 1. Найти производную второго порядка:
.
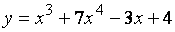Сначала найдем производную первого порядка:
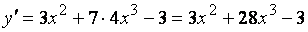. Теперь найдем производную от производной первого порядка. Это и будет производная второго порядка:
.
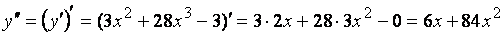Пример 2. Найти производную третьего порядка:
,
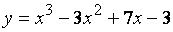Найдем производную первого порядка: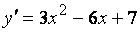 
, Теперь найдем производную второго порядка: 
.
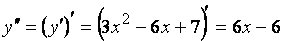И наконец найдем производную от производной второго порядка, это будет производная третьего порядка: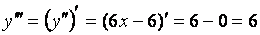 
.
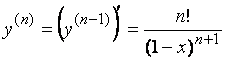
Пример 3. Найти значение третьей производной при х = 0 функции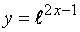 
.
Последовательно находим производные первого, второго, третьего порядков:
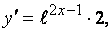
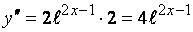
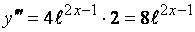
Найдем теперь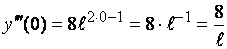 
.
Выполнить упражнения:
1) Найдите производную 5 порядка для функции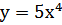 
2) 
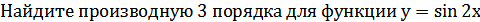
3) x(t)=2t3+t-1, найти t, когда a(t)=2
3. Задания самостоятельной работы.
1 вариант
1. Найдите производную 5 порядка для функции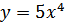 
2. Найдите производную 2 порядка для функции 
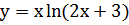3. x(t)=t3-4t2, a(5) -?
| 2 вариант
1. Найдите производную 3 порядка для функции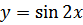 
2. Найдите производную 6 порядка для функции 
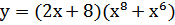3. x(t)=  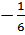t3 +3t2 – 5, найти t, когда a(t)=0
|
3 вариант
1. Найдите производную 2 порядка для функции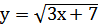 
2. Найдите производную 5 порядка для функции 
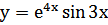3. x(t)=t5+3t2-1,a(2) -?
| 4 вариант
1. Найдите производную 5 порядка для функции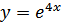 
2. Найдите производную 4 порядка для функции 
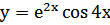3. x(t)=0,25t4-2t2, a(1) -?
|
4. Контрольные вопросы
1) Сформулируйте правила дифференцирования.
2) Что называется производной n-го порядка?
3) Механический смысл второй производной?
4) Найти производную n-го порядка функции y = ekx